Граф — это (конечное) множество точек и соединяющих эти точки отрезков. Точки называют вершинами, а отрезки — рёбрами. Граф называется связным, если любые две его вершины соединены ломанной. Граф называется полным, если любые две его вершины соединены ребром. Степенью вершины называется число выходящих из неё рёбер.
1. Если граф можно обойти, пройдя по каждому ребру ровно один раз, то в этом графе не более двух нечётных вершин. (теорема Эйлера)
2. a) Можно ли объединить 17 компьютеров в сеть так, чтобы каждый был бы соединён ровно с тремя другими?
b) В некотором государстве n городов и из каждого города выходит ровно 3 дороги. Может ли в этом государстве быть ровно 100 дорог?
3. Пусть в некотором графе n вершин и p рёбер. a) Найдите сумму степеней его вершин. b) Докажите, что число нечётных вершин в этом графе чётно.

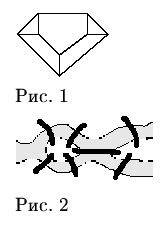
4. a) Можно ли прогуляться по парку, перейдя через каждый забор ровно один раз? (См. рис. 1.)
b) Гуляя по Кенигсбергу, Л. Эйлер захотел обойти город, пройдя по каждому мосту ровно один раз. Сможет ли он это сделать? (См. рис. 2.)
5. a) Докажите, что из куска проволоки длиной 120см нельзя, не разламывая её, сделать каркас куба с ребром длины 10см. b) Какое наименьшее число раз придётся сломать проволоку, чтобы изготовить каркас?
6. У царя Дадона было 3 сына. Из его потомков по мужской линии 100 имело по 2 сына, а остальные умерли бездетными. Сколько всего потомков было у царя Дадона?
7. a) Докажите, что при любой раскраске в два цвета полного графа с 6 вершинами в нём найдётся одноцветный треугольник. b) Докажите, что при любой раскраске в три цвета полного графа с 17 вершинами в нём найдётся одноцветный треугольник.