Математическое образование: вчера, сегодня, завтра…

Арнольд Владимир Игоревич
"Жесткие" и "мягкие" математические модели

4. Опасность многоступенчатого управления

Явление, описываемое в этом разделе, хорошо известно в теории управления техническими системами. Оно наблюдается в чрезвычайно общей ситуации, но здесь я опишу его в самой простой модели, заменяя лишь технические термины человеческими.

Пусть производство какого-либо продукта x управляется некоторым руководителем, принимающим решение о скорости производства:

=y.

В свою очередь, поведение руководителя у управляется руководителем второго ранга, принимающим решение о том, как нужно менять скорость производства:

=z.

В свою очередь, поведение руководителя второго ранга z управляется руководителем третьего ранга, и т. д. вплоть до генерального руководителя (ранга n).

Генеральный руководитель в нашей модели реализует обратную связь: его решение основывается не на желании выполнить приказ начальства (как у руководителей предыдущих рангов), а на интересах дела. Например, он может желать достичь уровня X величины x и будет влиять на руководителя предыдущего ранга в положительную сторону, если уровень x не достигнут, и в отрицательную -- если он превзойден.

Например, для n = 3 простейшая модель этого рода имеет вид



Эту систему можно переписать в виде линейного дифференциального уравнения порядка n:

x(n)= -k(x-X).

Уравнения этой (жесткой) модели легко решаются в явном виде. Устойчивость желаемого стационарного состояния (x= X, y= z= ... = 0) определяется тем, отрицательны ли вещественные части корней A характеристического уравнения

ln= -k.


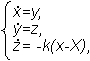
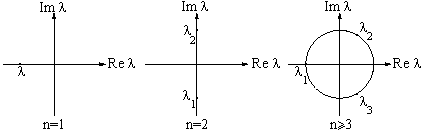Рис. 10. Неустойчивость многоступенчатого управления.

Эти корни -- комплексные числа, изображенные на рис. 10. Эти корни образуют на плоскости комплексного переменного l вершины правильного n-угольника. Если n > 3, некоторые вершины обязательно лежат в (неустойчивой) правой полуплоскости (Re l>0). При n =1 корень l=-k лежит в устойчивой полуплоскости, а при n= 2 корни l1,2= лежат на границе устойчивости.

Вывод. Многоступенчатое управление, описываемое нашей моделью при n>3, неустойчиво. Двухступенчатое управление приводит к периодическим колебаниям, но не вызывает катастрофического нарастания колебаний, происходящего при трех- и более ступенчатом управлении.

Настоящую устойчивость обеспечивает только одноступенчатое управление, при котором управляющее лицо более заинтересовано в интересах дела, чем в поощрении со стороны начальства.

Эти выводы, сделанные выше на основании анализа простейшей жесткой модели, на самом деле выдерживают проверку на структурную устойчивость, исключая лишь случай n= 2: двухступенчатое управление может оказаться как устойчивым, так и неустойчивым, в зависимости от деталей организации дела, которыми мы выше пренебрегли при составлении нашей самой простой модели.

Длительное и, по-видимому, устойчивое функционирование системы многоступенчатого управления в СССР объяснялось, вероятно, неисполнением директивных указаний и существованием "теневой" системы заинтересовывания управляющих различных рангов в интересах дела. Без такой реальной заинтересованности (которая в современных условиях уже не обязательно обеспечивается коррупцией) многоступенчатое управление всегда ведет к разрухе.

К счастью, необходимость в независимости Центробанка уже хорошо понята, но многоступенчатое ("административное") управление сохраняется во многих других случаях.

Следующий раздел