Глава 10. Задачи для самостоятельного решения  |	Оглавление |	Глава 11.

10.1.

Пусть медианы AA₁ и BB₁ пересекаются в точке M. Так как BC > AC, то точки A и C лежат по одну сторону от серединного перпендикуляра к отрезку AB, а значит, по ту же сторону лежат медиана CC₁ и ее точка M. Следовательно,  AM < BM, т. е. m_a < m_b.

10.2.

Предположим, например, что a > b. Тогда m_a < m_b (задача 10.1). А так как четырехугольник A₁MB₁C описанный, то  

a 2

+

mb 3

=

b 2

+

ma 3

, т. е. (a – b)/2 = (m_a – m_b)/3. Получено противоречие.

10.3.

Пусть, например,  BC > AC. Тогда MA < MB (см. задачу 10.1), поэтому  BC + MB + MC > AC + MA + MC.

10.4.

а) Так как c Ј a + b, то c² Ј (a + b)² = a² + b² + 2ab Ј 2(a² + b²).

10.5.

а) Пусть M- точка пересечения медиан,  O- центр описанной окружности треугольника ABC. Тогда  

AO2 + BO2 + CO2  =  (

® AM

+

® MO

)2 + (

® BM

+

® MO

)2 + (

® CM

+

® MO

)2 = AM2 + BM2 + CM2 + 2(

® AM

+

® BM

+

® CM

,

® MO

) + 3MO2

. Так как

® AM

+

® BM

+

® CM

=

® 0

, то  AO² + BO² + CO² = AM² + BM² + CM² + 3MO² і AM² + BM² + CM², т. е. 3R² і 4(m_a² + m_b² + m_c²)/9.

10.6.

Формулу Герона можно переписать в виде 16S² = 2a²b² + 2a²c² + 2b²c² – a⁴ – b⁴ – c⁴. А так как m_c² = (2a² + 2b² – c²)/4 (задача 12.11, а)), то неравенства m_c² Ј ((a² + b²)/2c)² и m_c² > ((a² – b²)/2c)² эквивалентны неравенствам 16S² Ј 4a²b² и 16S² > 0 соответственно.

10.7.

Пусть y = a² + b² + c² и y₁ = m_a² + m_b² + m_c². Тогда 3y = 4y₁ (задача 12.11, б)),  y < 2x (задача 9.7) и 2x₁ + y₁ < 2x + y, так как  (m_a + m_b + m_c)² < (a + b + c)² (см. задачу 9.2). Сложив неравенство 8x₁ + 4y₁ < 8x + 4y с равенством 3y = 4y₁, получим 8x₁ < y + 8x < 10x, т. е. x₁/x < 5/4.

10.8.

Ясно, что h_a Ј b, h_b Ј c, h_c Ј a, причем по крайней мере одно их этих неравенств строгое. Поэтому h_a + h_b + h_c < a + b + c.

10.9.

Пусть h_a > 1 и h_b > 1. Тогда a і h_b > 1. Поэтому S = ah_a/2 > 1/2.

10.10.

По условию BH і AC, а так как перпендикуляр короче наклонной, то BH і AC і AM. Аналогично AM і BC і BH. Поэтому BH = AM = AC = BC. Поскольку AC = AM, то отрезки AC и AM совпадают, т. е. РC = 90°, а так как AC = BC, то углы треугольника ABC равны 45, 45, 90°.

10.11.

Ясно, что  

1 ha

+

1 hb

=

a + b 2S

=

a + b (a + b + c)r

и  a + b + c < 2(a + b) < 2(a + b + c).

10.12.

Так как ah_a = 2S = r(a + b + c), то 

ha = r

ж и

1 +

b a

+

c a

ц ш

. Сложив такие равенства для h_a,h_b и h_c и воспользовавшись неравенством  

x y

+

y x

і 2

, получим требуемое.

10.13.

Так как h_a – h_b = 2S(1/a – 1/b) = 2S(b – a)/ab и 2S Ј ab, то h_a – h_b Ј b – a.

10.14.

Согласно задаче 12.21  

2 ha

=

1 rb

+

1 rc

. Кроме того,  

1 rb

+

1 rc

і 2/

Ц

rbrc

.

10.15.

Так как  2sin bsin g  = cos (b – g) – cos (b + g) Ј 1 + cos a, то 

ha a  =   sin bsin g sin a Ј  1 + cos a 2sin a  =   1 2 ctg   a 2 .

10.16.

Так как b/2R = sin b, то после домножения на 2p переходим к неравенству (a + b + c)(h_a + h_b + h_c) Ј 3sin b(a² + ac + c²). Вычитая из обеих частей 6S, получаем a(h_b + h_c) + b(h_a + h_c) + c(h_a + h_b) Ј 3sin b(a² + c²). Так как, например,  ah_b = a²sin g  = a²c/2R, переходим к неравенству a(b² + c²) – 2b(a² + c²) + c(a² + b²) Ј 0. Для доказательства последнего неравенства рассмотрим квадратный трехчлен  f(x) = x²(a + c) – 2x(a² + c²) + ac(a + c). Легко проверить, что  f(a) =  – a(a – c)² Ј 0 и  f(c) =  – c(a – c)² Ј 0. А так как коэффициент при x положителен и a Ј b Ј c, то f(b) Ј 0.

10.17.

Согласно задаче 12.35, а)  l_a² = 4bcp(p – a)/(b + c)². Кроме того,  4bc Ј (b + c)².

10.18.

Ясно, что h_a/l_a = cos ((b – g)/2). Согласно задаче 12.36, а)

2r/R = 8sin (a/2)sin (b/2)sin (g/2) = 4sin (a/2)[cos ((b – g)/2) –

– cos ((b + g)/2)] = 4x(q – x),    где   x = sin (a/2)   и   q = cos ((b – g)/2).

10.19.

а) Согласно задаче 10.17  l_a² Ј p(p – a). Складывая три аналогичных неравенства, получаем требуемое.

10.20.

Достаточно доказать, что  

Ц

p(p – a)

+

Ц

p(p – b)

+ mc Ј

Ц

3p

.
Можно считать, что p = 1; пусть x = 1 – a и y = 1 – b. Тогда  m_c² = (2a² + 2b² – c²)/4 = 1 – (x + y) + (x – y)²/4 = m(x,y). Рассмотрим функцию

f(x,y) = Цx + Цy +

Ц

m(x,y)

. Нужно доказать, что f(x,y) Ј Ц3 при x,y і 0 и x + y Ј 1. Пусть 

g(x) = f(x,x) = 2Цx +

Ц

1 – 2x

. Так как  

gў(x) =

1 Цx

–

1 Ц 1 – 2x

, то при возрастании x от 0 до 1/3  g(x) возрастает от 1 до Ц3, а при возрастании x от 1/3 до 1/2  g(x) убывает от Ц3 до Ц2. Введем новые переменные d = x – y и q = Цx + Цy. Легко проверить, что (x – y)² – 2q²(x + y) + q⁴ = 0, т. е. x + y = (d² + q⁴)/2q². Поэтому

f(x,y) = q +    ж Ц 1 –   q2 2  –   d2(2 – q2) 4q2   .

Заметим теперь, что  q² = (Цx + Цy)² Ј 2(x + y) Ј 2, т. е.  d²(2 – q²)/4q² і 0. Следовательно, при фиксированном q значение функции f(x,y) максимально, если d = 0, т. е. x = y; случай x = y разобран выше.

10.21.

Ясно, что  

1 a

+

1 b

+

1 c

= (ha + hb + hc)/2S

. Кроме того,  9r Ј h_a + h_b + h_c (задача 10.12) и h_a + h_b + h_c Ј m_a + m_b + m_c Ј 9R/2 (задача 10.5, б)).

10.22.

Докажем сначала, что b + c – a < 2bc/a. Пусть 2x = b + c – a,2y = a + c – b и 2z = a + b – c. Требуется доказать, что 2x < 2(x + y)(x + z)/(y + z), т. е. xy + xz < xy + xz + x² + yz. Последнее неравенство очевидно.

10.23.

Согласно задаче 12.30 a² + b² + c² = (a + b + c)² – 2(ab + bc + ac) = 4p² – 2r² – 2p² – 8rR = 2p² – 2r² – 8rR и abc = 4prR. Таким образом, нужно доказать неравенство  2p² – 2r² – 8rR < 2(1 – 4prR), где p = 1. Это неравенство очевидно.

10.24.

Согласно задаче 12.30 ab + bc + ca = r² + p² + 4Rr. Кроме того, 16Rr – 5r² Ј p² Ј 4R² + 4Rr + 3r² (задача 10.34).

10.25.

Так как r(ctg a + ctg b) = c = r_c(tg a + tg b), то 

c2 = rrc ж и 2 +   tg a tg b  +   tg b tg a ц ш і 4rrc.

10.26.

Достаточно воспользоваться результатами задач 12.36, а) и 10.45. Заметим также, что x(1 – x) Ј 1/4, т. е. r/R Ј 1/2.

10.27.

Так как h_c Ј a и h_c Ј b, то 4S = 2ch_c Ј c(a + b). Поэтому 6r(a + b + c) = 12S Ј 4ab + 4S Ј (a + b)² + c(a + b) = (a + b)(a + b + c).

10.28.

Так как 

2 ha

=

1 ra

+

1 rc

(задача 12.21), то  

ra ha

=

ж и

ra rb

+

ra rc

ц ш

/2

. Запишем аналогичные равенства для r_b/h_b и r_c/h_c и сложим их. Учитывая, что 

x y

+

y x

і 2

, получаем требуемое.

10.29.

Так как Rr = RS/p = abc/4p (см. задачу 12.1), то приходим к неравенству 27abc Ј 8p³ = (a + b + c)³.

10.30.

Так как OA = r/sin (A/2), OB = r/sin (B/2) и OC = r/sin (C/2), а углы РA/2, РB/2 и РC/2 острые, то РA Ј РB Ј РC. Следовательно, РA Ј 60° и РB Ј 90°, а значит,  sin (A/2) Ј 1/2 и sin (B/2) Ј 1/Ц2.

10.31.

Если РC і 120°, то сумма расстояний от любой точки внутри треугольника до его вершин не меньше a + b (задача 12.21); кроме того,  a + b і 6r (задача 12.27).

10.32.

Пусть a  = cos (A/2), b  = cos (B/2) и g  = cos (C/2). Согласно задаче 12.17, б)  a/r_a = a/bg, b/r_b = b/ga и c/r_c = g/ab. Поэтому после домножения на abg требуемое неравенство перепишется в виде  3(a² + b² + g²) і 4(b²g² + g²a² + a²b²). Так как a² = (1 + cos A)/2,b² = (1 + cos B)/2 и g² = (1 + cos C)/2, то переходим к неравенству cos A + cos B + cos C + 2(cos Acos B + cos Bcos C + cos Ccos A) Ј 3. Остается воспользоваться результатами задач 10.36 и 10.43.

10.33.

а) Сложив равенство 4R + r = r_a + r_b + r_c (задача 12.24) с неравенством R – 2r і 0 (задача 10.26), получим

5R – r і ra + rb + rc  =  pr((p – a) – 1 + (p – b) – 1 + (p – c) – 1)  =

=  p(ab + bc + ca – p2)/S  =  p(2(ab + bc + ca) – a2 – b2 – c2)/4S.

Остается заметить, что 2(ab + bc + ac) – a² – b² – c² і 4Ц3S (задача 10.54).

10.34.

Пусть a,b и c- длины сторон треугольника,  F = (a – b)(b – c)(c – a) = A – B, где A = ab² + bc² + ca² и B = a²b + b²c + c²a. Докажем, что требуемые неравенства можно получить, преобразовав очевидное неравенство F² і 0. Пусть s₁ = a + b + c = 2p,s₂ = ab + bc + ca = r² + p² + 4rR и s₃ = abc = 4prR (см. задачу 12.30). Можно проверить, что F² = s₁²s₂² – 4s₂³ – 4s₁³s₃ + 18s₁s₂s₃ – 27s₃². В самом деле,  (s₁s₂)² – F²  =  (A + B + 3abc)²-(A – B)² = 4AB + 6(A + B)s₃ + 9s₃² = 4(a³b³ + …) + 4(a⁴bc + …) + 6(A + B)s₃ + 21s₃². Ясно также, что  4s₂³ = 4(a³b³ + …) + 12(A + B)s₃ + 24s₃²,4s₁³s₃ = 4(a⁴bc + …) + 12(A + B)s₃ + 24s₃² и  18s₁s₂s₃ = 18(A + B)s₃ + 54s₃².

10.35.

Так как r_a + r_b + r_c = 4R + r и r_ar_b + r_br_c + r_cr_a = p² (задачи 10.24 и 10.25), то r_a² + r_b² + r_c² = (4R + r)² – 2p². Согласно задаче 10.34 p² Ј 4R² + 4Rr + 3r², поэтому r_a² + r_b² + r_c² і 8R² – 5r². Остается заметить, что r Ј R/2 (задача 10.26).

10.36.

а) Согласно задаче 12.38 cos a + cos b + cos g  = (R + r)/R. Кроме того,  r Ј R/2 (задача 10.26).

10.37.

а) Ясно, что sin a + sin b + sin g  = p/R. Кроме того,  p Ј 3Ц3 R/2 (задача 10.29).

10.38.

а) Согласно задаче 12.44, а) ctg a + ctg b + ctg g  = (a² + b² + c²)/4S. Кроме того,  a² + b² + c² і 4Ц3S (задача 10.53, б)).

10.39.

а) Согласно задаче 12.44, а) ctg (a/2) + ctg (b/2) + ctg (g/2) = p/r. Кроме того,  p і 3Ц3r (задача 10.53, а)).

10.40.

а) Согласно задаче 12.36, а) sin (a/2)sin (b/2)sin (g/2) = r/4R. Кроме того,  r Ј R/2 (задача 10.26).

10.41.

а) Так как  sin x = 2sin (x/2)cos (x/2), то, используя результаты задач 12.36, а) и 12.36, в), получаем  sin asin bsin g  = pr/2R². Кроме того,  p Ј 3Ц3R/2 (задача 10.29) и r Ј R/2 (задача 10.26).

10.42.

Согласно задаче 12.39, б)  cos ²a + cos ²b + cos ²g  = 1 – 2cos acos bcos g. Остается заметить, что  cos acos bcos g Ј 1/8 (задача 10.40, б)), а для тупоугольного треугольника  cos acos bcos g < 0.

10.43.

Ясно, что  2(cos acos b + cos bcos g + cos gcos a) = (cos a + cos b + cos g)² – cos ²a – cos ²b – cos ²g. Остается заметить, что  cos a + cos b + cos g Ј 3/2 (задача 10.36, а)) и cos ²a + cos ²b + cos ²g і 3/4 (задача 10.42).

10.44.

Пусть продолжения биссектрис остроугольного треугольника ABC с углами a,b и g пересекают описанную окружность в точках A₁,B₁ и C₁. Тогда S_ABC = R²(sin 2a + sin 2b + sin 2g)/2 и S_A1B1C1 = R²(sin (a + b) + sin (b + g) + sin (g + a))/2. Остается воспользоваться результатами задач 12.72 и 10.26.

10.45.

Ясно, что 2sin (b/2)sin (g/2) = cos ((b – g)/2) – cos ((b + g)/2) Ј 1 – sin (a/2).

10.46.

Опустим из вершин A и B перпендикуляры AA₁ и BB₁ на биссектрису угла ACB. Тогда AB і AA₁ + BB₁  =  bsin (g/2) + asin (g/2).

10.47.

Согласно задаче 12.32  tg (a/2)tg (b/2) = (a + b – c)/(a + b + c). А так как a + b < 3c, то a + b – c < (a + b + c)/2.

10.48.

Так как p – 2a > 0, p – 2b > 0, p – 2g > 0 и (p – 2a) + (p – 2b) + (p – 2g) = p, существует треугольник с углами p – 2a, p – 2b, p – 2g. Длины сторон, противолежащих углам p – 2a, p – 2b, p – 2g, пропорциональны числам sin (p – 2a) = sin 2a, sin 2b, sin 2g. Поскольку p – 2a > p – 2b > p – 2g и против большего угла лежит бóльшая сторона, то  sin 2a > sin 2b > sin 2g.

10.49.

Заметим сначала, что cos 2g – cos (p – a – b)  =  cos 2acos 2b – sin 2asin 2b. Поэтому cos 2a + cos 2b – cos 2g  = cos 2a + cos 2b – cos 2acos 2b + sin 2asin 2b. Так как 

acos j + bsin j Ј

Ц

a2 + b2

(см. приложение к гл. 9), то  

(1 – cos 2b)cos 2a + sin 2bsin 2a + cos 2b Ј

Ц

(1 – cos 2b)2 + sin 22b

+ cos 2b  = 2|sin b| + 1 – 2sin 2b

. Остается заметить, что наибольшее значение квадратного трехчлена 2t + 1 – 2t² достигается в точке t = 1/2 и равно 3/2. Максимальное значение соответствует углам a  = b  = 30°, g  = 120°.

10.50.

Так как AB < CB, AX < CX и S_ABX = S_BCX, то sin XAB > sin XCB. Учитывая, что угол XCB острый, получаем требуемое.

10.51.

Если углы треугольника ABC равны a,b и g, то углы треугольника A₁B₁C₁ равны (b + g)/2, (g + a)/2 и (a + b)/2.

10.52.

Пусть M- точка пересечения медиан AA₁,BB₁ и CC₁. Достроив треугольник AMB до параллелограмма AMBN, получим РBMC₁ = a_m и РAMC₁ = b_m. Легко проверить, что РC₁CB < g/2 и РB₁BC < b/2. Следовательно, a_m = РC₁CB + РB₁BC < (b + g)/2 < b. Аналогично g_m = РA₁AB + РB₁BA > (a + b)/2 > b.

Так как a > a_m, то a + (p – a_m) > p, т. е. точка M лежит внутри описанной окружности треугольника AB₁C₁. Следовательно,  g  = РAB₁C₁ < РAMC₁ = b_m. Аналогично a  = РCB₁A₁ > РCMA₁ = b_m, так как g + (p – g_m) < p.

10.53.

а) Ясно, что S²/p = (p – a)(p – b)(p – c) Ј ((p – a + p – b + p – c)/3)³ = p³/27. Поэтому pr = S Ј p²/3Ц3, т. е. r Ј p/3Ц3. Домножив последнее неравенство на r, получим требуемое.

10.54.

Пусть x = p – a, y = p – b, z = p – c. Тогда (a² – (b – c)²) + (b² – (a – c)²) + (c² – (a – b)²) = 4(p – b)(p – c) + 4(p – a)(p – c) + 4(p – a)(p – b)  =  4(yz + zx + xy) и 

4Ц3S  =  4 Ц   3p(p – a)(p – b)(p – c)    = 4 Ц   3(x + y + z)xyz   .

Итак, нужно доказать неравенство 

xy + yz + zx і

Ц

3(x + y + z)xyz

. После возведения в квадрат и сокращения получаем

x2y2 + y2z2 + z2x2 і x2yz + y2xz + z2xy.

Складывая неравенства x²yz Ј x²(y² + z²)/2,y²xz Ј y²(x² + z²)/2 и z²xy Ј z²(x² + y²)/2, получаем требуемое.

10.55.

а) Перемножив три равенства вида S = (absin g)/2, получим S³ = ((abc)²sin gsin bsin a)/8. Остается воспользоваться результатом задачи 10.41.

Так как (r_ar_br_c)² = S⁴/r² (задача 12.18, в) и r²(Ц3)³ Ј S (задача 10.53, а)), то (r_ar_br_c)² і (Ц3S)³.

10.56.

Пусть p = BA₁/BC, q = CB₁/CA и r = AC₁/AC. Тогда S_A1B1C1/S_ABC = 1 – p(1 – r) – q(1 – p) – r(1 – q)  =  1 – (p + q + r) + (pq + qr + rp). По теореме Чевы (задача 5.77) pqr = (1 – p)(1 – q)(1 – r), т. е. 2pqr = 1 – (p + q + r) + (pq + qr + rp); кроме того, (pqr)² = p(1 – p)q(1 – q)r(1 – r) Ј (1/4)³. Следовательно,

SA1B1C1/SABC = 2pqr Ј

1 4

.

10.57.

Можно считать, что площадь треугольника ABC равна 1. Тогда a + b + c = 1 – u, поэтому данное неравенство перепишется в виде u² і 4abc. Пусть x = BA₁/BC, y = CB₁/CA и z = AC₁/AB. Тогда u = 1 – (x + y + z) + xy + yz + zx и abc = xyz(1 – x)(1 – y)(1 – z) = v(u – v), где v = xyz. Поэтому мы переходим к неравенству u² і 4v(u – v), т. е. (u – 2v)² і 0. Последнее неравенство очевидно.

10.58.

а) Пусть x = BA₁/BC, y = CB₁/CA и z = AC₁/AB. Можно считать, что площадь треугольника ABC равна 1. Тогда S_AB1C1 = z(1 – y), S_A1BC1 = x(1 – z) и S_A1B1C = y(1 – x). Так как x(1 – x) Ј 1/4, y(1 – y) Ј 1/4 и z(1 – z) Ј 1/4, то произведение чисел S_AB1C1, S_A1BC1 и S_A1B1C не превосходит (1/4)³, а значит, одно из них не превосходит 1/4.

10.59.

Достаточно доказать, что если AC < BC, то РABC < РBAC. Так как AC < BC, то на стороне BC можно выбрать точку A₁ так, что A₁C = AC. Тогда РBAC > РA₁AC  =  РAA₁C > РABC.

10.60.

Пусть A₁- середина стороны BC. Если AA₁ < BC/2 = BA₁ = A₁C, то РBAA₁ > РABA₁ и РCAA₁ > РACA₁, поэтому РA = РBAA₁ + РCAA₁ > РB + РC, т. е. РA > 90°. Аналогично, если AA₁ > BC/2, то РA < 90°.

10.61.

Если мы фиксируем две стороны треугольника, то чем больше будет угол между ними, тем больше будет третья сторона. Поэтому из неравенства РA > РA₁ следует, что BD > B₁D₁, т. е. РC > РC₁. Предположим теперь, что РB і РB₁. Тогда AC і A₁C₁, т. е. РD > РD₁. Поэтому 360° = РA + РB + РC + РD > РA₁ + РB₁ + РC₁ + РD₁ = 360°. Получено противоречие; следовательно,  РB < РB₁ и РD < РD₁.

10.62.

Пусть точка B₁ симметрична B относительно точки M. Так как высота, опущенная из точки M на сторону BC, равна половине AH, т. е. половине BM, то РMBC = 30°. Поскольку AH- наибольшая из высот, то BC- наименьшая из сторон. Поэтому AB₁ = BC Ј AB, т. е. РABB₁ Ј РAB₁B = РMBC = 30°. Следовательно,  РABC = РABB₁ + РMBC Ј 30° + 30° = 60°.

10.63.

Предположим сначала, что РA > РD. Тогда BE > EC и РEBA < РECD. Так как в треугольнике EBC сторона BE больше стороны EC, то РEBC < РECB. Поэтому РB = РABE + РEBC < РECD + РECB = РC, что противоречит условию задачи. Значит,  РA = РB = РC = РD. Аналогично предположение РB > РE приводит к неравенству РC < РD. Поэтому РB = РC = РD = РE.

10.64.

Будем проводить доказательство сразу для общего случая. Пусть прямая MN пересекает стороны многоугольника в точках M₁ и N₁. Ясно, что MN Ј M₁N₁. Пусть точка M₁ лежит на стороне AB, а точка N₁- на PQ. Так как РAM₁N₁ + РBM₁N₁ = 180°, то один из этих углов не меньше 90°. Пусть для определенности РAM₁N₁ і 90°. Тогда AN₁ і M₁N₁, так как против большего угла лежит бóльшая сторона. Аналогично доказывается, что либо AN₁ Ј AP, либо AN₁ Ј AQ. Следовательно, длина отрезка MN не превосходит длины отрезка с концами в вершинах многоугольника.

10.65.

Отрезок можно продолжить до пересечения с границей сектора, так как при этом его длина только увеличится. Поэтому можно  считать, что точки M и N лежат на границе сектора. Возможны три случая.

2. Точки M и N лежат на отрезках AO и BO. Тогда MN не превосходит наибольшей стороны треугольника AOB.

3. Одна из точек M и N лежит на дуге окружности, а другая- на отрезке AO или BO. Пусть для определенности M лежит на AO, а N- на дуге окружности. Тогда MN не превосходит наибольшей стороны треугольника ANO. Остается заметить, что AO = NO = R и AN Ј AB.

10.66.

Если данный отрезок не имеет общих точек с окружностью, то с помощью гомотетии с центром A (и коэффициентом больше 1) его можно перевести в отрезок, имеющий общую точку X с дугой AB и лежащий в нашей области. Проведем через точку X касательную DE к окружности (точки D и E лежат на отрезках AB и AC). Тогда отрезки AD и AE меньше AB и DE < (DE + AD + AE)/2 = AB, т. е. все стороны треугольника ADE меньше AB. Так как наш отрезок лежит внутри треугольника ADE (или на его стороне DE), то его длина не превосходит AB.

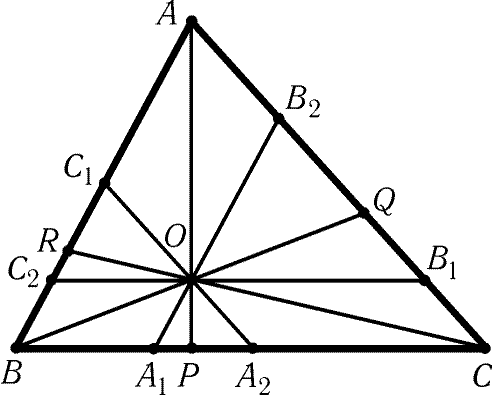
Рис. 10.1

10.67. Предположим сначала, что центр O окружности лежит внутри данного пятиугольника A₁A₂A₃A₄A₅. Рассмотрим углы  A₁OA₂, A₂OA₃,…, A₅OA₁. В сумме эти пять углов дают 2p, поэтому один из них, например A₁OA₂, не превосходит 2p/5. Тогда отрезок A₁A₂ можно поместить в сектор OBC, где РBOC = 2p/5 и точки B и C расположены на окружности. В треугольнике OBC наибольшей стороной является BC, поэтому A₁A₂ Ј BC.

Если точка O не принадлежит данному пятиугольнику, то углы A₁OA₂,…, A₅OA₁ дают в объединении угол меньше p, причем каждая точка этого угла покрыта ими дважды. Поэтому в сумме эти пять углов дают меньше 2p, т. е. один из них меньше 2p/5. Дальнейшее доказательство аналогично предыдущему случаю.

Если точка O лежит на стороне пятиугольника, то один из рассматриваемых углов не больше p/4, а если она является его вершиной, то один из них не больше p/3. Ясно, что p/4 < p/3 < 2p/5.

10.68.

Возьмем на сторонах BC, CA, AB точки A₁ и A₂,  B₁ и B₂,  C₁ и C₂ так, что B₁C₂||BC, C₁A₂||CA,A₁B₂||AB (рис. 10.1). В треугольниках A₁A₂O, B₁B₂O, C₁C₂O наибольшими сторонами являются A₁A₂, B₁O, C₂O соответственно. Поэтому OP < A₁A₂, OQ < B₁O, OR Ј C₂O, т. е.  OP + OQ + OR < A₁A₂ + B₁O + C₂O = A₁A₂ + CA₂ + BA₁ = BC.

10.69.

Так как c² = a² + b², то cⁿ = (a² + b²)c^n – 2  =  a²c^n – 2 + b²c^n – 2 > aⁿ + bⁿ.

10.70.

Высота любого треугольника больше 2r. Кроме того, в прямоугольном треугольнике 2r = a + b – c (задача 5.16).

10.71.

Так как ch = 2S = r(a + b + c) и 

c =

Ц

a2 + b2

, то  

r h

=

Ц a2 + b2 a + b +  Ц a2 + b2

=

1 x + 1

, где  

x =

a + b Ц a2 + b2

=

ж Ц

1 +   2ab a2 + b2

. Так как 0 < 2ab/(a² + b²) Ј 1, то 1 < x Ј Ц2. Следовательно,  2/5 < 1/(1 + Ц2) Ј r/h < 1/2.

10.72.

Ясно, что 

a + b і 2

Ц

ab

и c² = a² + b² і 2ab. Поэтому

c2 r2  =   (a + b + c)2c2 a2b2 і (2 Ц   ab    +  Ц   2ab   )2 · 2ab a2b2  =  4(1 + Ц2)2.

10.73.

Согласно задаче 12.11,  а)  m_a² + m_b²  = (4c² + a² + b²)/4 = 5c₂/4. Кроме того,  5c²/4 і 5(1 + Ц2)²r²  =  (15 + 10Ц2)r² > 29r² (см. задачу 10.72).

10.74.

Пусть O- центр описанной окружности,  A₁,B₁,C₁- середины сторон BC, CA, AB соответственно. Тогда m_a = AA₁ Ј AO + OA₁ = R + OA₁. Аналогично m_b Ј R + OB₁ и m_c Ј R + OC₁. Следовательно,

ma ha  +   mb hb  +   mc hc Ј R ж и  1 ha  +   1 hb  +   1 hc ц ш  +   OA1 ha  +   OB1 hb  +   OC1 hc .

Остается воспользоваться результатом задачи 12.22 и решением задачи 4.46.

10.75.

Согласно задаче 4.47  

1 b

+

1 c

=

2cos (a/2) la

і

Ц2 la

. Складывая три аналогичных неравенства, получаем требуемое.

10.76.

Обозначим точку пересечения медиан через M, а центр описанной окружности через O. Если треугольник ABC не тупоугольный, то точка O лежит внутри его (или на его стороне); для определенности будем считать, что она лежит внутри треугольника AMB. Тогда AO + BO Ј AM + BM, т. е. 2R Ј 2m_a/3 + 2m_b/3 или m_a + m_b і 3R. Остается заметить, что так как угол COC₁ (C₁- середина AB) тупой, то CC₁ і CO, т. е. m_c і R.

10.77.

В любом треугольнике h_b Ј l_b Ј m_b (см. задачу 2.68), поэтому h_a = l_b і h_b и m_c = l_b Ј m_b. Следовательно,  a Ј b и b Ј c (см. задачу 10.1), т. е. c - наибольшая сторона, а g- наибольший угол.

10.78.

Согласно задаче 1.60 отношение периметров треугольников A₁B₁C₁ и ABC равно r/R. Кроме того,  r Ј R/2 (задача 10.26).

10.79.

Пусть AA₁ и BB₁ - биссектрисы треугольников OAH и OBH. Согласно задаче 2.1 они являются биссектрисами углов A и B, т.е. центр вписанной окружности - точка пересечения прямых AA₁ и BB₁. Из неравенства AC > BC следует, что AH > BH. Поэтому

A1H/A1O = AH/AO > BH/BO = B1H/B1O,

т. е. точки на прямой OH расположены в таком порядке: O, A₁, B₁, H. Точка O лежит внутри треугольника ABH, поэтому точка пересечения прямых AA₁ и BB₁ лежит внутри треугольника BOH.

10.80.

Пусть 90° і a і b і g. Тогда CH- наибольшая высота. Центры вписанной и описанной окружностей обозначим через I и O, точки касания вписанной окружности со сторонами BC,CA,AB- через K,L,M соответственно (рис. 10.2).

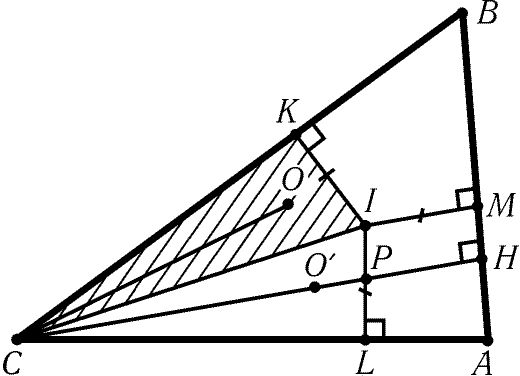
Рис. 10.2

Докажем сначала, что точка O лежит внутри треугольника KCI. Для этого достаточно доказать, что CK і KB и РBCO Ј BCI. Ясно, что CK = rctg (g/2) і rctg (b/2) = KB и 2РBCO  =  180° – РBOC = 180° – 2a Ј 180° – a – b  = g  = 2РBCI. Так как РBCO = 90° – a  = РACH, при симметрии относительно CI прямая CO переходит в прямую CH. Пусть Oў- образ точки O при этой симметрии,  P- точка пересечения CH и IL. Тогда CP і COў = CO = R. Остается доказать, что PH і IM = r. Это следует из того, что РMIL = 180° – a і 90°.

10.81. Пусть B₂C₂- проекция отрезка B₁C₁ на сторону BC. Тогда B₁C₁ і B₂C₂ = BC – BC₁cos b – CB₁cos g. Аналогично A₁C₁ і AC – AC₁cos a – CA₁cos g и A₁B₁ і AB – AB₁cos a – BA₁cos b. Домножим эти неравенства на cos a, cos b и cos g соответственно и сложим их. Получим B₁C₁cos a + C₁A₁cos b + A₁B₁cos g і acos a + bcos b + ccos g – (acos bcos g + bcos acos g + ccos acos b). Так как c = acos b + bcos a, то ccos g = acos bcos g + bcos acos g. Записав три аналогичных неравенства и сложив их, получим acos bcos g + bcos acos g + ccos acos b  = (acos a + bcos b + ccos g)/2.

10.82.

Так как cos ²a + cos ²b + cos ²g + 2cos acos bcos g  = 1 (задача 12.39, б)), то треугольник ABC остроугольный тогда и только тогда, когда cos ²a + cos ²b + cos ²g < 1, т. е. sin ²a + sin ²b + sin ²g > 2. Домножая обе части последнего неравенства на 4R², получаем требуемое.

10.83.

Достаточно заметить, что p² – (2R + r)²  =  4R²cos acos bcos g (см. задачу 12.41, б)).

10.84.

Пусть РA Ј РB Ј РC. Если треугольник ABC не остроугольный, то CC₁ < AC < AA₁ для любых точек A₁ и C₁ на сторонах BC и AB. Докажем теперь, что для остроугольного треугольника можно выбрать точки A₁,B₁ и C₁, обладающие требуемым свойством. Для этого достаточно проверить, что существует число x, удовлетворяющее следующим неравенствам:

ha Ј x <

max

(b,c) = c

,

hb Ј x <

max

(a,c) = c

и 

hc Ј x <

max

(a,b) = b

. Остается заметить, что 

max

(ha,hb,hc) = ha

,  

min

(b,c) = b

и h_a < b.

10.85.

Пусть РA Ј РB Ј РC. Предположим сначала, что треугольник ABC остроугольный. При повороте прямой l, в исходном положении параллельной AB, длина проекции треугольника на l будет сначала монотонно изменяться от c до h_b, затем от h_b до a, от a до h_c, от h_c до b, от b до h_a и, наконец, от h_a до c. Так как h_b < a, то существует такое число x, что h_b < x < a. Легко проверить, что отрезок длиной x встречается на любом из первых четырех интервалов монотонности.

10.86.

Пусть точки M и N лежат на сторонах AB и AC соответственно. Проведем через вершину C прямую, параллельную стороне AB. Пусть N₁- точка пересечения этой прямой и прямой MN. Тогда N₁O : MO = 2, но NO Ј N₁O, поэтому NO : MO Ј 2.

10.87.

Окружность S, вписанная в треугольник ABC, лежит внутри треугольника AўBўCў. Проведя к этой окружности касательные, параллельные сторонам треугольника AўBўCў, можно получить треугольник AўўBўўCўў, подобный треугольнику AўBўCў, для которого S является вписанной окружностью. Поэтому r_ABC = r_{AўўBўўCўў} < r_AўBўCў.

10.88.

Биссектриса l_c разбивает треугольник ABC на два треугольника, удвоенные площади которых равны al_csin (g/2) и bl_csin (g/2). Поэтому ah_a = 2S = l_c(a + b)sin (g/2). Из условия задачи следует, что a/(a + b) Ј 1/2 Ј sin (g/2).

10.89.

Ясно, что ctg A + ctg B = c/h_c і c/m_c. Пусть M - точка пересечения медиан,  N- середина отрезка AB. Так как треугольник AMB прямоугольный,  MN = AB/2. Следовательно,  c = 2MN = 2m_c/3.

10.90.

Так как BN · BA = BM² и BM < BA, то BN < BM, а значит,  AN > CN.

10.91.

Проведем через точку B перпендикуляр к стороне AB. Пусть F- точка пересечения этого перпендикуляра с продолжением стороны AC (рис. 10.3). Докажем, что биссектриса AD, медиана BM и высота CH пересекаются в одной точке тогда и только тогда, когда AB = CF. В самом деле, пусть L- точка пересечения BM и CH. Биссектриса AD проходит через точку L тогда и только тогда, когда BA : AM = BL : LM, но BL : LM = FC : CM  =  FC : AM.

Рис. 10.3

10.92.

Так как против большей стороны лежит больший угол, то (a – b)(a – b) і 0, (b – c)(b – g) і 0 и (a – c)(a – g) і 0. Складывая эти неравенства, получаем

2(aa + bb + cg) і a(b + g) + b(a + g) + c(a + b) = (a + b + c)p – aa – bb-cg,

т. е. p/3 Ј (aa + bb + cg)/(a + b + c).

10.93.

Возьмем на лучах OB и OC такие точки C₁ и B₁, что OC₁ = OC и OB₁ = OB. Пусть B₂ и C₂- проекции точек B₁ и C₁ на прямую, перпендикулярную AO. Тогда BOsin AOC + COsin AOB = B₂C₂ Ј BC. Сложив три аналогичных неравенства, получим требуемое. Легко проверить также, что условие B₁C₁^AO,C₁A₁^BO и A₁B₁^CO эквивалентно тому, что O- точка пересечения биссектрис.

10.94.

Так как РCBD = РC/2 и РB і РA, то  РABD = РB + РCBD і (РA + РB + РC)/2 = 90°.

10.95.

По свойству биссектрисы BM : MA = BC : CA и BK : KC = BA : AC. Поэтому BM : MA = BK : KC, т. е.

AB AM  = 1 +   BM MA < 1 +   BK KC  =   CB CK .

Следовательно, точка M более удалена от прямой AC, чем точка K, т. е. РAKM > РKAC = РKAM и РKMC < РMCA  =  РMCK. Поэтому AM > MK и MK > KC (см. задачу 10.59).

10.96.

Предположим, что все данные отношения меньше 2. Тогда S_ABO + S_AOC < 2S_XBO + 2S_XOC = 2S_OBC,S_ABO + S_OBC < 2S_AOC и S_AOC + S_OBC < 2S_ABO. Сложив эти неравенства, приходим к противоречию. Аналогично доказывается, что одно из данных соотношений не больше 2.

10.97.

Обозначим радиусы окружностей S,S₁ и S₂ через r,r₁ и r₂. Пусть треугольники AB₁C₁ и A₂BC₂ подобны треугольнику ABC, причем коэффициенты подобия равны r₁/r и r₂/r соответственно. Окружности S₁ и S₂ являются вписанными для треугольников AB₁C₁ и A₂BC₂. Следовательно, эти треугольники пересекаются, так как иначе окружности S₁ и S₂ не имели бы общих точек. Поэтому AB₁ + A₂B > AB, т. е. r₁ + r₂ > r.

Глава 10. Задачи для самостоятельного решения  |	Оглавление |	Глава 11.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.