| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
§ 7. Вычисление углов
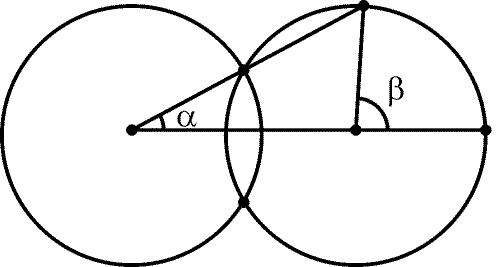
Рис. 12.2
12.50. Даны две пересекающиеся окружности радиуса R, причем
расстояние между их центрами больше R. Докажите, что b
= 3a
(рис. 12.2).
12.51. Докажите, что если
,
то РA = 120°.
12.52. В треугольнике ABC высота AH равна медиане BM.
Найдите угол MBC.
-
12.53.
-
В треугольнике ABC проведены биссектрисы AD
и BE. Найдите величину угла C, если известно, что AD · BC = BE · AC и AC № BC.
12.54. Найдите угол B треугольника ABC, если длина
высоты CH равна половине длины стороны AB, а РBAC = 75°.
-
12.55*.
-
В прямоугольном треугольнике ABC с прямым углом A
на высоте AD как на диаметре построена окружность, пересекающая
сторону AB в точке K и сторону AC в точке M. Отрезки AD
и KM пересекаются в точке L. Найдите острые углы
треугольника ABC, если известно, что AK : AL = AL : AM.
-
12.56*.
-
В треугольнике ABC угол C вдвое больше угла A
и b = 2a. Найдите углы этого треугольника.
-
12.57*.
-
В треугольнике ABC проведена биссектриса BE
и на стороне BC взята точка K так, что РAKB = 2РAEB. Найдите
величину угла AKE, если РAEB = a.
-
12.58*.
-
В равнобедренном треугольнике ABC с основанием BC
угол при вершине A равен 80°. Внутри треугольника ABC
взята точка M так, что РMBC = 30° и РMCB = 10°. Найдите величину угла AMC.
-
12.59*.
-
В равнобедренном треугольнике ABC с основанием AC
угол при вершине B равен 20°. На сторонах BC и AB взяты
точки D и E соответственно так, что РDAC = 60°
и РECA = 50°. Найдите угол ADE.
-
12.60*.
-
В остроугольном треугольнике ABC отрезки BO и CO,
где O- центр описанной окружности, продолжены до пересечения
в точках D и E со сторонами AC и AB. Оказалось, что РBDE = 50° и РCED = 30°. Найдите величины углов
треугольника ABC.
Глава 12. § 6 | 
