
 Глава 12. § 7 |
Глава 12. § 7 | 
| Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
 |
||
 Глава 12. § 7 | Глава 12. § 7 | |
Оглавление | | Глава 12. § 9  |
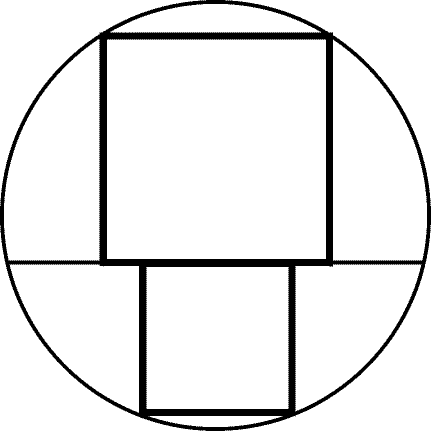
Рис. 12.3
12.62*. Пусть E- середина стороны AB квадрата ABCD, а точки F и G выбраны на сторонах BC и CD так, что AG||EF. Докажите, что отрезок FG касается окружности, вписанной в квадрат ABCD.
12.63*. Хорда окружности удалена от центра на расстояние h. В каждый из сегментов, стягиваемых хордой, вписан квадрат так, что две соседние вершины квадрата лежат на дуге, а две другие- на хорде или ее продолжении (рис. 12.3). Чему равна разность длин сторон этих квадратов?
12.64*. Найдите отношение сторон треугольника, одна из медиан которого делится вписанной окружностью на три равные части.
| * * * |
|
 Глава 12. § 7 | Глава 12. § 7 | |
Оглавление | | Глава 12. § 9  |
 |
| Copyright © 2002 МЦНМО |
Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru. |
|