Глава 12. Задачи для самостоятельного решения  |	Оглавление |	Глава 13.

12.1.

По теореме синусов sin g  = c/2R, поэтому S = (absin g)/2 = abc/4R.

12.2.

Радиусы описанных окружностей треугольников ABD и CBD равны AB/2sin ADB и BC/2sin BDC. Остается заметить, что AB = BC и sin ADB = sin BDC.

12.3.

По теореме синусов b = asin b/sin a  = asin b/sin (b + g), поэтому S = absin g/2 = a²sin bsin g/2sin (b + g).

12.4.

По теореме синусов (a + b)/c = (sin a + sin b)/sin g. Кроме того, sin a + sin b  = 2sin ((a + b)/2)cos ((a – b)/2) = 2cos (g/2)cos ((a – b)/2) и sin g  = 2sin (g/2)cos (g/2). Второе равенство доказывается аналогично.

12.5.

В треугольнике A₂BC₂ длины сторон A₂B и BC₂ равны bcos g и bcos a; прямая BO делит угол A₂BC₂ на углы 90° – g и 90° – a. Пусть прямая BO пересекает отрезок A₂C₂ в точке M. По теореме синусов A₂M = A₂Bsin A₂BM/sin A₂MB = bcos gcos a/sin C₂MB = C₂M.

12.6.

Пусть a  = Р(a, c), b  = Р(c, d) и g  = Р(d, b). Тогда

(AC/AS)/(BC/BS) = sin a/sin (b + g),     (BD/BS)/(AD/AS)  =  sin g/sin (a + b).

Поэтому

(AC · BD)/(BC · AD)  =  sin asin g/sin (a + b) sin (b + g).

12.7.

Так как OA/PA = sin OPA/sin POA и OB/PB = sin OPB/sin POB, то (OA/OB)/(PA/PB) = sin POB/sin POA.

12.8.

Достаточно перемножить пять равенств вида D₁A/D₁B = sin B/sin A.

12.9.

Пусть O - общая вершина данных треугольников, M и N- середины оснований, k - отношение длин оснований к высотам. Проекции оснований данных треугольников на прямую MN равны k · OMsin OMN и k · ONsin ONM. Остается заметить, что OM/sin ONM = ON/sin OMN.

12.10.

По теореме синусов BX/sin BDX = BD/sin BXD = 2R sin y/sin BXD. Кроме того, sin BDX = sin BDC = sin j; величина угла BXD легко вычисляется: если точки C и D лежат по одну сторону от AB, то РBXD = p – j – y, а если по разные, то РBXD  =  |j – y|. Значит, BX = 2Rsin jsin y/sin |j±y|.

12.11.

а) Пусть A₁- середина отрезка BC. Складывая равенства AB² = AA₁² + A₁B² – 2AA₁ · BA₁cos BA₁A и AC² = AA₁² + A₁C² – 2AA₁ · A₁C cos CA₁A и учитывая, что cos BA₁A =  – cos CA₁A, получаем требуемое.

12.12.

По теореме косинусов a² – (b – c)² = 2bc(1 – cos a) = 4S(1 – cos a)/sin a  = 4Stg (a/2).

12.13.

По теореме косинусов cos a  = (b² + c² – a²)/2bc. Остается воспользоваться формулами cos ²(a/2) = (1 + cos a)/2 и sin ²(a/2) = (1 – cos a)/2.

12.14.

Пусть a - угол при вершине параллелограмма. По теореме косинусов m² = a² + b² + 2abcos a и n² = a² + b² – 2abcos a. Поэтому m²n² = (a² + b²)² – (2abcos a)² = a⁴ + b⁴ + 2a²b²(1 – 2cos ²a). Значит, m²n² = a⁴ + b⁴ тогда и только тогда, когда cos ²a  = 1/2.

12.15.

Пусть M - точка пересечения медиан AA₁ и BB₁. Угол AMB прямой тогда и только тогда, когда AM² + BM² = AB², т. е. 4(m_a² + m_b²)/9 = c². Согласно задаче 12.11 m_a² + m_b²  =  (4c² + a² + b²)/4.

12.16.

Пусть m = C₁M и j  = РC₁MO. Тогда OC₁² = C₁M² + OM² – 2OM · C₁Mcos j и BO² = CO² = OM² + MC² + 2OM · CMcos j  = OM² + 4C₁M² + 4OM · C₁Mcos j. Поэтому BC₁² = BO² – OC₁²  =  3C₁M² + 6OM · C₁Mcos j, т. е. c² = 4BC₁² = 12m² + 24OM · C₁Mcos j. Ясно также, что 18 m² = 2m_c² = a² + b² – c²/2 (см. задачу 12.21). Поэтому равенство a² + b² = 2c² эквивалентно тому, что 18m² = 3c²/2, т. е. c² = 12m². Так как c² = 12m² + 24OM · C₁Mcos j, равенство a² + b² = 2c² эквивалентно тому, что РC₁MO = j  = 90°, т. е. CC₁^OM.

12.17.

Пусть вписанная окружность касается стороны BC в точке K, а вневписанная - в точке L. Тогда BC = BK + KC = rctg (b/2) + rctg (g/2) и BC = BL + LC = r_actg LBO_a + r_actg LCO_a = r_atg (b/2) + r_atg (g/2). Кроме того,

cos (a/2) = sin

ж и

b 2

+

g 2

ц ш

.

Если вписанная окружность касается продолжений сторон AB и AC в точках P и Q, то p = AP = AQ = r_actg (a/2).

12.18.

а) Согласно задаче 12.17 p = r_actg (a/2) и rctg (a/2) = p – a; rctg (b/2) = p – b и r_atg (b/2) = p – c; r_ctg (b/2) = p – a и r_bctg (b/2) = p. Перемножая эти пары равенств, получаем требуемое.

в) Достаточно перемножить равенства rr_a = (p – b)(p – c) и r_br_c = p(p – a) и воспользоваться формулой Герона.

12.19.

Согласно задаче 12.17 r = r_ctg (a/2)tg (b/2) и p = r_cctg (g/2).

12.20.

Согласно задаче 12.18, а) r_a = rp/(p – a) и r_b = rp(p – b). Поэтому cr_ar_b = cr²p²/((p – a)(p – b)) и r_a + r_b = rpc/((p – a)(p – b)), а значит, cr_ar_b/(r_a + r_b) = rp = S.

12.21.

Согласно задаче 12.18, а) 1/r_b = (p – b)/pr и 1/r_c = (p – c)/pr. Поэтому

1 rb

+

1 rc

= a/pr = a/S = 2/ha

.

12.22.

Легко проверить, что 1/h_a = a/2pr и 1/r_a = (p – a)/pr. Складывая аналогичные равенства, получаем требуемое.

12.23.

Согласно задаче 12.18, а) 1/((p – b)(p – c)) = 1/rr_a. Остается сложить аналогичные равенства и воспользоваться результатом задачи 12.22.

12.24.

Согласно задаче 12.1 4SR = abc. Ясно также, что

abc = p(p – b)(p – c) + p(p – c)(p – a) + p(p – a)(p – b) –

– (p – a)(p – b)(p – c) =   S2 (p – a)  +   S2 (p – b)  +   S2 (p – c)  –   S2 p  = S(ra + rb + rc – r).

12.25.

Согласно задаче 12.18, а) r_ar_b = p(p – c), r_br_c = p(p – a) и r_cr_a = p(p – b). Складывая эти равенства, получаем требуемое.

12.26.

Так как S = rp = r_a(p – a) = r_b(p – b) = r_c(p – c), то выражение в правой части равно (p³ – (p – a)³ – (p – b)³ – (p – c)³)/S³ = 3abc/S³. Остается заметить, что abc/S = 4R (задача 12.1).

12.27.

Пусть углы треугольника ABC равны 2a, 2b и 2g. Согласно задачам 12.36, а) и 12.37, б)  r = 4Rsin asin bsin g и r_a = 4Rsin acos bcos g. Поэтому (r + r_a)(4R + r – r_a) = 16R²sin a (sin bsin g + cos bcos g)(1 + sin a(sin bsin g – cos bcos g)) = 16R²sin acos (b – g)(1 – sin acos (b + g))  =  16R²sin acos (b – g)cos ²a. Остается заметить, что 4Rsin acos a  = a и 4Rsin (b + g)cos (b – g)  =  2R(sin 2b + sin 2g) = b + c. Второе равенство доказывается аналогично.

12.28.

Так как OA = r/sin (a/2) и bc = 2S/sin a, то OA²/bc = r²ctg (a/2)/S = r(p – a)/S (см. задачу 12.17, в). Остается заметить, что r(p – a + p – b + p – c) = rp = S.

12.29.

Решим сразу задачу б), частным случаем которой является задача а). Так как ctg (j/2) = sin j/(1 – cos j), то p²(1 – x)² = (1 – x²)(2R(1 – x) + r)², где x = cos j. Корень x₀ = 1 этого уравнения нас не интересует, так как в этом случае ctg (j/2) был бы не определен; поэтому, сократив обе части уравнения на 1 – x, придем к кубическому уравнению. Использовав результаты задач 12.38, 12.41, б), можно проверить, что это уравнение совпадает с уравнением (x – cos a)(x – cos b)(x – cos g) = 0, где a,b и g- углы треугольника. Значит, косинус угла j равен косинусу одного из углов треугольника; кроме того, косинус монотонен на интервале от 0 до p.

12.30.

Ясно, что 2pr = 2S = absin g = abc/2R, т. е. 4prR = abc. Для доказательства второго равенства воспользуемся формулой Герона:  S² = p(p – a)(p – b)(p – c), т. е. pr² = (p – a)(p – b)(p – c) = p³ – p²(a + b + c) + p(ab + bc + ca) – abc =  – p³ + p(ab + bc + ca) – 4prR. Сокращая на p, получаем требуемое.

12.31.

Так как abc = 4RS (задача 12.1), то выражение в левой части равно (c + a + b)/4RS = 2p/4Rpr = 1/2Rr.

12.32.

Достаточно заметить, что (p – c)/p = r/r_c (задача 12.18, а)),  r = csin (a/2)sin (b/2)/cos (g/2) и r_c = ccos (a/2)cos (b/2)/cos (g/2) (задача 12.17).

12.33.

Согласно задаче 12.1  S = abc/4R. С другой стороны,  S = ah_a/2. Поэтому h_a = bc/2R.

12.34.

Так как ah_a = 2S = 2(p – a)r_a и r_a/a = cos (b/2)cos (g/2)/cos (a/2) (задача 12.17, б)), то h_a = 2(p – a)cos (b/2)cos (g/2)/cos (a/2). Учитывая, что (p – a)ctg (b/2) = r_c = (p – b)ctg (a/2) (задача 12.17, в)), получаем h_a = 2(p – b)sin (b/2)cos (g/2)/sin (a/2).

12.35.

а) Пусть продолжение биссектрисы AD пересекает описанную окружность треугольника ABC в точке M. Тогда AD · DM = BD · DC и,  так как DABD ~ DAMC, AB · AC = AD · AM = AD(AD + DM) = AD² + BD · DC. Кроме того,  BD = ac/(b + c) и DC = ab/(b + c). Значит, AD² = bc – bca²/(b + c)² = 4p(p – a)bc/(b + c)².

в) Пусть AD- биссектриса,  AH- высота треугольника ABC. Тогда AH = csin b  = 2Rsin bsin g. С другой стороны,  AH = ADsin ADH  =  l_asin (b + (a/2)) = l_asin ((p + b – g)/2) = l_acos ((b – g)/2).

г) Учитывая, что p = 4Rcos (a/2)cos (b/2)cos (g/2) (задача 12.36, в) и sin b + sin g  = 2sin ((b + g)/2)cos ((b – g)/2) = 2cos (a/2)cos ((b – g)/2), приходим к формуле задачи в).

12.36.

а) Пусть O- центр вписанной окружности,  K- точка касания вписанной окружности со стороной AB. Тогда

2Rsin g = AB = AK + KB = r(ctg (a/2) + ctg (b/2))  =

=  rsin ((a + b)/2)(sin (a/2)sin (b/2)).

Учитывая, что sin g  = 2sin (g/2)cos (g/2) и sin ((a + b)/2)  =  cos (g/2), получаем требуемое.

в) Очевидным образом следует из задач а) и б).

12.37.

а) Перемножая равенства

rcos (a/2)sin (a/2) = p – a,    sin (a/2)sin (b/2)sin (g/2) = r/4R

(см. задачи 12.17, в) и 12.36, а)), получаем требуемое.

12.38.

Складывая равенства cos a + cos b  = 2cos ((a + b)/2)cos ((a – b)/2) и cos g  =  – cos (a + b) =  – 2cos ²((a + b)/2) + 1 и учитывая, что cos ((a – b)/2) – cos ((a + b)/2)  =  2sin (a/2)sin (b/2), получаем cos a + cos b + cos g  = 4sin (a/2)×

×sin (b/2)sin (g/2) + 1 =

r R

+ 1

(см. задачу 12.36, а)).

12.39.

а) Складывая равенства cos 2a + cos 2b = 2cos (a + b)cos (a – b) =  – 2cos gcos (a – b) и cos 2g  = 2cos ²g – 1 =  – 2cos gcos (a – b) – 1 и учитывая, что cos (a + b) + cos (a – b) = 2cos acos b, получаем требуемое.

12.40.

Складывая равенства sin 2a + sin 2b  = 2sin (a + b)cos (a – b) = 2sin g×
×cos (a – b) и sin 2g  = 2sin gcos g  =  – 2sin gcos (a + b) и учитывая, что cos (a – b) – cos (a + b)  =  2sin asin b, получаем требуемое.

12.41.

а) Ясно, что sin ²a + sin ²b + sin ²g  = (a² + b² + c²)/4R и a² + b² + c² = (a + b + c)² – 2(ab + bc + ca)  =  4p² – 2(r² + p² + 4rR) (см. задачу 12.30).

12.42.

Теорему косинусов можно переписать в виде abcos g  = (a² + b² – c²)/2. Складывая три аналогичных равенства, получаем требуемое.

12.43.

Согласно задаче 12.13  cos ²(a/2)/a = p(p – a)/abc. Остается заметить, что p(p – a) + p(p – b) + p(p – c) = p² и abc = 4SR = 4prR.

12.44.

а) Так как bccos a  = 2Sctg a, то a² = b² + c² – 4Sctg a. Складывая три аналогичных равенства, получаем требуемое.

12.45.

Согласно задаче 12.17  ctg (a/2) + ctg (b/2) = c/r и tg (a/2) + tg (b/2) = c/r_c. Остается сложить такие равенства для всех пар углов треугольника.

12.46.

Ясно, что tg g  =  – tg (a + b) =  – (tg a + tg b)/(1 – tg atg b). Домножая обе части на 1 – tg atg b, получаем требуемое.

12.47.

tg (g/2) = ctg

ж и

a 2

+

b 2

ц ш

= [1 – tg (a/2)tg (b/2)] [tg (a/2) + tg (b/2)].

Остается домножить обе части на tg (a/2) + tg (b/2).

12.48.

а) Домножим обе части равенства на sin asin bsin g. Дальнейший ход доказательства таков:  cos g(sin acos b + sin bcos a) + sin g(cos acos b – sin asin b) = cos gsin (a + b) + sin gcos (a + b) = cos gsin g – sin gcos g  = 0.

12.49.

Так как sin ²a + sin ²b + sin ²g – 2  =  2cos acos bcos g (см. задачу 12.39, б)) и S = 2R²sin asin bsin g, остается проверить, что (tg a + tg b + tg g)× ×cos acos bcos g  = sin gsin bsin a. Последнее равенство доказано в решении задачи 12.48, а).

12.50.

Пусть A и B- вершины углов a и b,  P- точка пересечения несовпадающих сторон этих углов,  Q- общая точка данных окружностей, лежащая на отрезке PA. Треугольник AQB равнобедренный, поэтому РPQB = 2a. А так как РPQB + РQPB = b + РQBA, то b  = 3a.

12.51.

Согласно задаче 4.47  

1 b

+

1 c

= 2cos (a/2)/la

, поэтому cos (a/2) = 1/2, т. е. a  = 120°.

12.52.

Опустим из точки M перпендикуляр MD на прямую BC. Тогда MD = AH/2 = BM/2. В прямоугольном треугольнике BDM катет MD равен половине гипотенузы BM. Поэтому РMBC = РMBD = 30°.

12.53.

Величины AD · BCsin ADB и BE · ACsin AEB равны, так как они равны удвоенной площади треугольника ABC. Поэтому sin ADB = sin AEB. Возможны два случая.

2. РADB + РAEB = 180°; в этом случае РECD + РEOD = 180°, где O- точка пересечения биссектрис. Так как РEOD = 90° + РC/2 (задача 5.3), то РC  =  60°.

12.54.

Пусть Bў- точка пересечения серединного перпендикуляра к отрезку AC с прямой AB. Тогда ABў = CBў и РABўC = 180° – 2 · 75° = 30°. Поэтому ABў = CBў = 2CH = AB, т. е. Bў = B и РB = 30°.

12.55.

Ясно, что AKDM- прямоугольник и L- точка пересечения его диагоналей. Так как AD^BC и AM^BA, то РDAM = РABC. Аналогично,  РKAD = РACB. Опустим из точки A перпендикуляр AP на прямую KM. Пусть для определенности РB < РC. Тогда точка P лежит на отрезке KL. Из подобия треугольников AKP и MKA получаем AK :  AP = MK : MA. Поэтому AK · AM = AP · MK = AP · AD  =  2AP · AL. По условию AL² = AK · AM, следовательно,  AL = 2AP, т. е. РALP = 30°. Ясно, что РKMA = РALP/2 = 15°. Поэтому острые углы треугольника ABC равны 15 и 75°.

12.56.

Пусть CD- биссектриса. Тогда BD = ac/(a + b). С другой стороны,  DBDC ~ DBCA, поэтому BD :  BC = BC : BA, т. е. BD = a²/c. Следовательно,  c² = a(a + b) = 3a². Стороны треугольника ABC равны a,2a и Ц3a, поэтому его углы равны 30,90 и 60°.

12.57.

Пусть РABC = 2x, тогда внешний угол A треугольника ABE равен РABE + РAEB = x + a. Далее, РKAE – РBAK = (180° – x – a) – (180° – 2x – 2a) = x + a. Следовательно,  AE- биссектриса внешнего угла Aтреугольника ABK.А так как BE — биссектриса внутреннего угла B этого треугольника, то E- центр его вневписанной окружности, касающейся стороны AK. Поэтому РAKE = РAKC/2 = 90° – a.

12.58.

Пусть A₁… A₁₈- правильный восемнадцатиугольник. В качестве треугольника ABC можно взять треугольник A₁₄A₁A₉. Согласно задаче 6.62, б) диагонали A₁A₁₂,A₂A₁₄ и A₉A₁₈ пересекаются в одной точке, поэтому РAMC = (ИA₁₈A₂ + ИA₉A₁₄)/2 = 70°.

12.59.

Пусть A₁… A₁₈- правильный восемнадцатиугольник,  O- его центр. В качестве треугольника ABC можно взять треугольник A₁OA₁₈. Диагонали A₂A₁₄ и A₁₈A₆ симметричны относительно диаметра A₁A₁₀, а диагональ A₂A₁₄ проходит через точку пересечения диагоналей A₁A₁₂ и A₉A₁₈ (см. решение предыдущей задачи), поэтому РADE = (ИA₁A₂ + И A₁₂A₁₄)/2 = 30°.

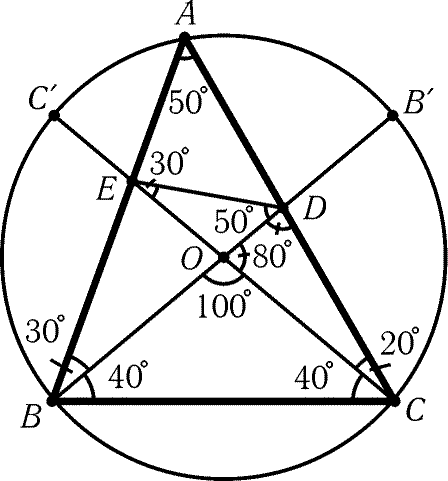
Рис. 12.6

12.60. Поскольку РBDE = 50° и РCED = 30°, то РBOC = РEOD = 180° – 50° – 30° = 100°. Будем считать, что фиксированы диаметры BBў и CCў окружности, причем РBOC = 100°, а точка A движется по дуге BўCў. Пусть D- точка пересечения BBў и AC,  E- точка пересечения CCў и AB (рис. 12.6). Так как при движении точки A от Bў к Cў отрезок OE увеличивается, а OD уменьшается, то угол OED убывает, а угол ODE возрастает. Поэтому существует единственное положение точки A, при котором РCED = РOED = 30° и РBDE = РODE = 50°.

Докажем теперь, что треугольник ABC с углами РA = 50°,РB = 70°, РC = 60° обладает требуемым свойством. Пусть A₁… A₁₈- правильный восемнадцатиугольник. В качестве треугольника ABC можно взять треугольник A₂A₁₄A₉. Диагональ A₁A₁₂ проходит через точку E (см. решение задачи 12.58). Пусть F- точка пересечения прямых A₁A₁₂ и A₅A₁₄; прямая A₉A₁₆ симметрична прямой A₁A₁₂ относительно прямой A₅A₁₄, поэтому она проходит через точку F. В треугольнике CDF луч CE является биссектрисой угла C, а прямая FE- биссектрисой внешнего угла при вершине F. Поэтому DE- биссектриса угла ADB, т. е. РODE  =  (ИA₂A₁₄ + ИA₅A₉)/4 = 50°.

12.61.

Пусть D,E и F- точки касания окружности с BP,PQ и QC;   РBOD = 90° – РB = 90° – РC = РCOF = a, РDOP = РPOE = b и РEOQ = РQOF = g. Тогда 180° = РBOC = 2a + 2b + 2g, т. е. a + b + g  = 90°. Так как РBPO = РDPE/2 =  (180° – РDOE)/2 = 90° – b и РQOC = g + a  = 90° – b, то РBPO = РCOQ. Ясно также, что РPBO = РOCQ. Поэтому DBPO ~ DCOQ, т. е. PB · CQ = BO · CO = BC²/4.

12.62.

Пусть P и Q- середины сторон BC и CD соответственно. Точки P и Q являются точками касания вписанной окружности со сторонами BC и CD. Поэтому достаточно проверить, что PF + GQ = FG. В самом деле, если FўGў- отрезок, параллельный FG и касающийся вписанной окружности, то PFў + GўQ = FўGў, поэтому Fў = F и Gў = G.

Рис. 12.7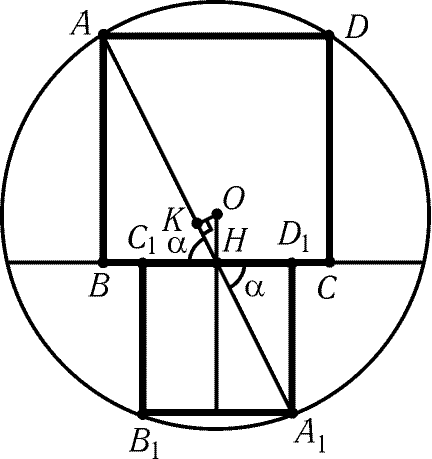

12.63. Обозначим вершины квадратов так, как показано на рис. 12.7. Пусть O- центр окружности,  H- середина данной хорды,  K- середина отрезка AA₁. Так как  = tg AHB = 2 = tg  A₁HD₁, то точка H лежит на прямой AA₁. Пусть a  = РAHB  =  РA₁HD₁. Тогда AB – A₁D₁ = (AH – A₁H)sin a  = 2KHsin a  = 2OHsin ²a. Поскольку tg a  = 2 и 1 + ctg ²a  = 1/sin ²a, то sin ²a  = 4/5. Поэтому разность длин сторон квадратов равна 8h/5.

12.64. Пусть медиана BM треугольника ABC пересекает вписанную окружность в точках K и L, причем BK = KL = LM = x. Пусть для определенности тоска касания вписанной окружности со стороной AC лежит на отрезке MC. Тогда, так как при симметрии относительно серединного перпендикуляра к отрезку BM точки B и M переходят друг в друга, а вписанная окружность переходит в себя, касательная MC переходит в касательную BC. Следовательно,  BC = MC = AC/2, т. е. b = 2a.

Так как BM² = (2a² + 2c² – b²)/4 (см. задачу 12.11, а)), то 9x² = (2a² + 2c² – 4a²)/4 = (c² – a²)/2. Пусть точка P- точка касания вписанной окружности со стороной BC. Тогда BP = (a + c – b)/2  =  (c – a)/2. С другой стороны, по свойству касательной BP² = BK · BL, т. е. BP² = 2x². Поэтому 2x² = ((c – a)/2)². Перемножая равенства 9x² = (c² – a²)/2 и ((c – a)/2)² = 2x², получаем (c + a)/(c – a) = 9/4, т. е. c : a = 13 : 5. В итоге получаем, что a : b : c = 5 : 10 : 13.

12.65.

Пусть 2a и 2b- длины сторон первого и второго квадратов. Тогда расстояние от центра окружности до вершин второго квадрата, лежащих на окружности, равно 

Ц

(a + 2b)2 + b2

. С другой стороны, это расстояние равно Ц2a. Следовательно,  (a + 2b)² + b² = 2a², т. е. 

a = 2b±

Ц

4b2 + 5b2

= (2±3)b

. Нам подходит только решение a = 5b.

12.66.

Пусть P и Q- середины отрезков AC и AB,  R- центр окружности S₁;  a = AC/2, b = BC/2,  x- радиус окружности S₁. Легко проверить, что PR = a + x, QR = a + b – x и PQ = b. Проведем в треугольнике PQR высоту RH. Расстояние от точки R до прямой CD равно x, поэтому PH = a – x, а значит,  QH = |b – a + x|. Следовательно,  (a + x)² – (a – x)² = RH² = (a + b – x)² – (b – a + x)², т. е. ax = b(a – x). В итоге получаем x = ab/(a + b). Для радиуса окружности S₂ получаем точно такое же выражение.

12.67.

Пусть x- радиус окружности S, касающейся окружностей S₁ и S₂ и луча AB,  y- радиус окружности Sў, касающейся окружностей S₂ и S₃ и луча BA. Положение окружности, касающейся окружности S₁ и луча AB (соответственно S₃ и луча BA) однозначно определяется ее радиусом, поэтому достаточно проверить, что x = y.

Рассматривая окружности S₂ и S₃, легко проверить, что AB² = (3 + 4)² – 1² = 48. С другой стороны, квадраты расстояний от центра окружности Sў до прямых AD и BC равны (y + 3)² – (5 – y)²  =  16(y – 1) и (4 + y)² – (4 – y)² = 16y соответственно. Следовательно,  

4

Ц

y – 1

+ 4Цy =

Ц

48

, т. е. y = 4/3.

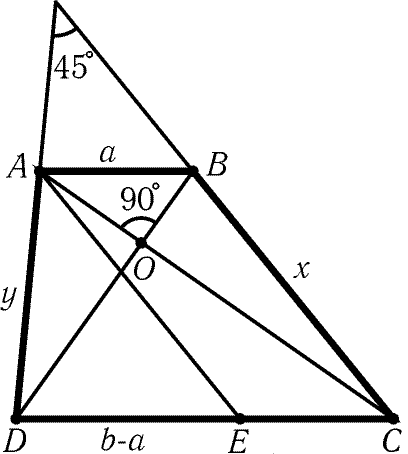
Рис. 12.8

12.68. Если углы треугольника образуют арифметическую прогрессию, то они равны a – g, a, a + g, где g і 0. Так как сумма углов треугольника равна 180°, то a  = 60°. Стороны этого треугольника равны 2Rsin (a – g), 2Rsin a,2Rsin (a + g). Поскольку против большего угла лежит бóльшая сторона, то sin (a – g) Ј sin a Ј sin (a + g).

а) Если числа sin (a – g) Ј sin a Ј sin (a + g) образуют арифметическую прогрессию, то sin a  = (sin (a + g) + sin (a – g))/2 = sin acos g, т. е. cos g  = 1, или g  = 0. Следовательно, все углы треугольника равны 60°.

б) Если числа sin (a – g) Ј sin a Ј sin (a + g) образуют геометрическую прогрессию, то sin ²a  = sin (a – g)sin (a + g) = sin ²acos ²g – sin ²gcos ²a Ј sin²acos ²g. Поэтому cos g  = 1, т. е. все углы треугольника равны 60°.

12.69.

Достроим треугольник ABC до параллелограмма ABCE (рис. 12.8). Пусть BC = x и AD = y. Тогда (b – a)h = 2S_AED = xysin 45° и (b – a)² = x² + y² – 2xycos 45° = x² + y² – 2xysin 45°. По теореме Пифагора a² + b² = (AO² + BO²) + (CO² + DO²) = (BO² + CO²) + (DO² + AO²) = x² + y². Следовательно,  (b – a)² = x² + y² – 2xysin 45° = a² + b² – 2(b – a)h, т. е. h = ab/(b – a).

12.70.

Так как BK = (a + c – b)/2 и KC = (a + b – c)/2 (см. задачу 3.2), то BK · KC = (a² – (b – c)²)/4 = Stg (a/2) (см. задачу 12.12).

12.71.

Так как (b + c)/a = cos ((b – g)/2)/sin (a/2) (задача 12.4), то cos ((b – g)/2) = cos (a/2), т. е. b – g = ±a. Если b = g + a, то b = 90°, а если b + a = g, то g = 90°.

12.72.

Легко проверить, что S_ABC = 2R²sin asin bsin g. Аналогично  S_A1B1C1 = 2R²sin ((b + g)/2)sin ((a + g)/2)sin ((a + b)/2) = 2R²cos (a/2)cos (b/2)cos (g/2). Поэтому  S_ABC/S_A1B1C1 = 8sin (a/2)sin (b/2)sin (g/2) = 2r/R (см. задачу 12.36, а).

12.73.

Сумма котангенсов углов треугольника равна (a² + b² + c²)/4S (задача 12.44, а)). Кроме того,  m_a² + m_b² + m_c² = 3(a² + b² + c²)/4 (задача 12.11, б)) и площадь треугольника, составленного из медиан треугольника ABC, равна 3/4 площади треугольника ABC (задача 1.37).

12.74.

Одна из точек A_i лежит внутри треугольника, образованного тремя другими точками, поэтому можно считать, что треугольник A₁A₂A₃ остроугольный (или прямоугольный). Числа l₁, l₂ и l₃ легко находятся из соответствующей системы уравнений; в результате получаем l₁ = (b² + c² – a²)/2,l₂ = (a² + c² – b²)/2 и l₃ = (a² + b² – c²)/2, где a = A₂A₃,b = A₁A₃ и c = A₁A₂. Согласно задаче 5.47, б)  A₁A₄² = 4R² – a², где R- радиус описанной окружности треугольника A₁A₂A₃. Поэтому  l₄ = A₁A₄² – l₁ = 4R² – (a² + b² + c²)/2  =  A₂A₄² – l₂ = A₃A₄² – l₃.

12.75.

Пусть (a₁,b₁), (a₂,b₂) и (a₃,b₃)- координаты вершин треугольника. Координаты центра его описанной окружности задаются системой уравнений

(x – a1)2 + (y – b1)2 = (x – a2)2 + (y – b2)2,

(x – a1)2 + (y – b1)2 = (x – a3)2 + (y – b3)2.

Легко проверить, что эти уравнения линейные, а значит, решение рассматриваемой системы уравнений рационально.

12.76.

Возьмем на отрезках AB и CD точки K и L, делящие их в указанных отношениях. Достаточно доказать, что точка пересечения прямых AK и CL лежит на окружности S. Введем систему координат с началом в центре O окружности S и осями Ox и Oy, направленными по лучам OB и OD. Радиус окружности S можно считать равным 1. Прямые AK и CL задаются соответственно уравнениями y = (x + 1)/3 и y = 2x – 1. Поэтому их общая точка имеет координаты x₀ = 4/5 и y₀ = 3/5. Ясно, что x₀² + y₀² = 1.

12.77.

Пусть d- расстояние от центра описанной окружности до образа центра вписанной окружности при рассматриваемой гомотетии. Достаточно проверить, что R = d + 2r. Пусть (0,0), (2a,0) и (0,2b)- координаты вершин данного треугольника. Тогда (a,b) - координаты центра описанной окружности,  (r,r) - координаты центра вписанной окружности, причем r = a + b – R. Следовательно,  d² = (2r – a)² + (2r – b)² = a² + b² – 4r(a + b – r) + 4r² = (R – 2r)², так как a² + b² = R².

12.78.

Рассмотрим систему координат с началом в центре квадрата и осью Ox, параллельной прямой l. Пусть вершины квадрата имеют следующие координаты:  A(x,y), B(y, – x), C( – x, – y) и D( – y,x); прямая l задается уравнением y = a. Тогда точка Q имеет координаты ((x + y)/2, (y – x)/2), а точка P имеет координаты ( – y,a). Следовательно, искомое ГМТ состоит из точек (t, – t + a/2), где t = (x – y)/4. Остается заметить, что величина x – y изменяется от 

–

Ц

2(x2 + y2)

=  – AB

до AB.

Глава 12. Задачи для самостоятельного решения  |	Оглавление |	Глава 13.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.