| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
18.1.
-
Повернем квадрат ABCD относительно точки A на 90°
так, чтобы точка B перешла в точку D. При этом повороте точка M
переходит в точку Mў, а точка K - в точку Kў. Ясно, что
РBMA = РDMўA. Так как РMAK = РMAB = РMўAD, то РMAD = РMўAK. Поэтому
РMўAK = РMAD = РBMA = РDMўA, а значит,
AK = KMў = KD + DMў = KD + BM.
-
18.2.
-
При повороте на 90° относительно точки P прямые PA1,
PB1, PM1 и CH переходят в прямые, параллельные CA, CB, CM
и AB соответственно. Следовательно, при таком повороте треугольника
PA1B1 отрезок PM1 переходит в медиану (повернутого) треугольника.
-
18.3.
-
Рассмотрим поворот на 90° относительно точки B, переводящий
вершину K в вершину N, а вершину C - в A. При этом
повороте точка A переходит в некоторую точку Aў точка E - в Eў.
Так как Eў и B - середины сторон AўN и AўC треугольника
AўNC, то BEў||NC. Но РEBEў = 90°, поэтому BE^NC.
-
18.4.
-
При повороте относительно центра квадрата на 90°, переводящем
точку A1 в точку A2, перпендикуляры, опущенные из
точек A1, A2, A3 и A4,
переходят в прямые A2P, A3P,
A4P и A1P соответственно. Поэтому точкой их пересечения является
образ точки P при обратном повороте.
-
18.5.
-
Повернем данный квадрат вокруг точки A на 90° так, чтобы
вершина B перешла в D. Пусть Mў - образ точки M при этом
повороте. Так как по условию MK + MC + CK = (BM + MC) + (KD + CK),
то MK = BM + KD = DMў + KD = KMў. Кроме того, AM = AMў, поэтому
DAMK = DAMўK, а значит, РMAK = РMўAK = РMAMў/2 = 45°.
-
18.6.
-
Пусть R - поворот на 90°, переводящий вектор
в
. Пусть, далее,
,
и
. Тогда
,
и
. Поэтому
|
®
D2D1
|
= Rb – a + Ra + Rc
|
и
.
Следовательно,
, так как
R(Ra) = – a.
-
18.7.
-
Введем следующие обозначения:
,
;
Ra и Rb - векторы, полученные из векторов a
и b поворотом на 90°:
,
; O1, O2, O3 и O4 - середины
отрезков AM, MQ, QC и CA соответственно. Тогда
,
,
,
.
Поэтому
|
®
O1O2
|
= (Rb – Ra)/2 = – |
®
O3O4
|
|
и
|
®
O2O3
|
= (b – a)/2 = – |
®
O4O1
|
|
. Кроме того,
.
-
18.8.
-
Вокруг квадрата ABCD описан параллелограмм A1B1C1D1
(точка A лежит на стороне A1B1, B - на B1C1 и т. д.).
Опустим из вершин A1, B1, C1 и D1 перпендикуляры l1,
l2, l3 и l4 на стороны квадрата. Чтобы доказать, что эти
прямые образуют квадрат, достаточно проверить, что при повороте на
90° относительно центра O квадрата ABCD прямые l1, l2,
l3 и l4 переходят друг в друга. При повороте относительно точки O
на 90° точки A1, B1, C1 и D1 переходят в точки A2,
B2, C2 и D2 (рис. 18.1).

Рис. 18.1
Так как AA2^B1B и BA2^B1A, то B1A2^AB.
Это означает, что прямая l1 переходит при повороте на 90°
относительно точки O в прямую l2. Для остальных прямых доказательство
аналогично.
18.9.
При повороте вокруг точки C на 60° точка A
переходит в B1, а точка A1 - в B. Поэтому отрезок
AA1 переходит в отрезок B1B.
18.10.
Рассмотрим поворот на 60° относительно точки C, переводящий
точку E в D. При этом точка B переходит в A, т. е.
отрезок BE переходит в отрезок AD. Поэтому середина P отрезка
BE переходит в середину M отрезка AD, т. е. треугольник CPM
равносторонний.
18.11.
Предположим, что мы построили треугольник ABC так,
что его вершины A, B и C лежат на прямых l1, l2 и l3
соответственно. При повороте на 60° с центром A точка B
переходит в точку C, поэтому C - точка пересечения прямой l3
и образа прямой l2 при повороте на 60° с центром A.
18.12.
Искомое ГМТ состоит из двух квадратов, полученных из
данного квадрата поворотами на ±60° с центром P.
18.13.
При повороте на 60° векторы
и
переходят
в
и
. Следовательно, при этом повороте
вектор
переходит в вектор
.
18.14.
Пусть Mў - образ точки M при повороте на 60° относительно
точки B, переводящем A в C. Тогда РCMўB = РAMB = 120°.
Треугольник MMўB равносторонний, поэтому РBMўM = 60°.
Так как РCMўB + РBMўM = 180°, точка Mў лежит на
отрезке MC. Поэтому MC = MMў + MўC = MB + MA.
18.15.
При повороте на 60° с центром A, переводящем B в C,
точка M переходит в некоторую точку Mў, а точка C - в точку D.
Равенство MA2 = MB2 + MC2 эквивалентно равенству
MўM2 = MўC2 + MC2, т. е. тому, что РMCMў = 90°, а значит,
РMCB + РMBC = РMCB + РMўCD = 120° – 90° = 30°, т. е. РBMC = 150°. Искомое ГМТ - дуга
окружности, лежащая внутри треугольника, из которой отрезок BC виден
под углом 150°.
-
18.16.
-
Пусть O - центр шестиугольника. Рассмотрим поворот с центром A
на 60°, переводящий точку B в O. При этом
повороте отрезок OC переходит в отрезок FE. Точка K является
серединой диагонали BD параллелограмма BCDO, поэтому она
является серединой диагонали CO. Следовательно, точка K при
нашем повороте переходит в точку M, т. е. треугольник AMK
правильный.
18.17.
При повороте на 60° относительно центра данного шестиугольника,
переводящем вершину A в B, отрезок CD переходит в DE, поэтому
точка M переходит в N. Таким образом, при этом повороте отрезок AM
переходит в BN, т. е. угол между этими отрезками равен 60°.
Кроме того, при этом повороте пятиугольник AMDEF переходит в BNEFA,
т. е. их площади равны. Вырезая из этих равновеликих пятиугольников их
общую часть, пятиугольник APNEF, получаем две равновеликие фигуры:
треугольник ABP и четырехугольник MDNP.
18.18.
Рассмотрим поворот на 60° с центром C, переводящий
точку B в A. При этом точки M, N и D переходят в Mў, Nў
и Dў. Так как AMNNў - параллелограмм, середина E диагонали
AN является его центром симметрии. Поэтому при симметрии
относительно точки E треугольник BMN переходит в MўANў, а значит,
точка D переходит в Dў, т. е. E - середина отрезка DDў. А так
как треугольник CDDў правильный, то углы треугольника CDE равны
30°, 60° и 90°.
18.19.
Рассмотрим поворот с центром A, переводящий точку C1
в точку B. При этом повороте правильный треугольник A1BC
переходит в треугольник A2FB1,
а отрезок A1C1 переходит в отрезок
A2B. Остается заметить, что BA1A2B1 - параллелограмм, т. е.
середина отрезка A2B совпадает с серединой отрезка A1B1.
18.20.
Пусть
,
. Пусть, далее, R -
поворот, переводящий вектор
в
(а значит,
вектор
- в
).
Тогда
и
. Легко проверить,
что b + R2b = Rb. Поэтому
,
а из этого соотношения вытекает требуемое.
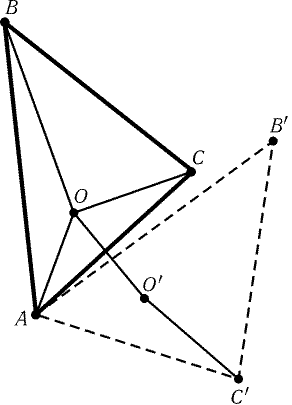
Рис. 18.2
18.21.
При повороте относительно точки C на 60° против часовой
стрелки точка A переходит в точку B, точка D - в точку E,
а значит, вектор
переходит в вектор
.
Так как при повороте относительно точки H на 60° против часовой
стрелки точка K переходит в точку E и вектор
переходит
в вектор
, то точка D при этом повороте переходит в точку B,
т. е. треугольник BHD равносторонний.
18.22.
а) Пусть O - точка внутри треугольника ABC. При повороте на
60° относительно точки A точки B, C и O переходят в
некоторые точки Bў, Cў и Oў (рис. 18.2). Так как AO = OOў и OC = OўCў,
то BO + AO + CO = BO + OOў + OўCў. Длина ломаной BOOўCў минимальна тогда,
когда эта ломаная является отрезком, т. е. РAOB = РAOўCў = РAOC = 120°. Для построения искомой точки можно
воспользоваться результатом задачи 2.8.
б) Сумма расстояний от точки O до вершин равна длине
отрезка BCў, полученного при решении задачи а). Ясно также, что
(BCў)2 = b2 + c2 – 2bccos (a + 60°) = b2 + c2 – bccos a + bcЦ3sin a
= (a2 + b2 + c2)/2 + 2Ц3 S.
18.23.
Пусть O - центр правильного треугольника ABC,
и
. Тогда
и
, где a = 120°. Поэтому
|
|
®
XA
|
+ Ra( |
®
XB
|
) + R2a( |
®
XC
|
) = (x + a) + (Rax + R2aa) + (R2ax + Raa) = |
|
|
= (x + Rax + R2ax) + (a + Raa + R2aa) = 0. |
|
Это означает, что векторы
,
и
являются векторами сторон некоторого
треугольника. Вырожденность треугольника эквивалентна сонаправленности двух их
этих векторов. Если, например, векторы
и
, то Р(AX,XB) = Р(AC,CB), поэтому
точка X лежит на описанной окружности треугольника ABC. Вырожденность
треугольника в том случае, когда точка X лежит на описанной окружности,
доказана в задаче 18.14.
-
18.24.
-
Пусть P, Q и R - середины сторон BC, DE и FA,
O - центр описанной окружности. Предположим, что треугольник
PQR правильный. Докажем, что тогда середины сторон BC, DEў
и FўA
шестиугольника ABCDEўFў,
в котором вершины Eў и Fў
получены из точек E и F поворотом на некоторый угол относительно
точки O, тоже образуют правильный треугольник. Этим будет все
доказано, так как для правильного шестиугольника середины сторон
BC, DE и FA образуют правильный треугольник, а любой из
рассматриваемых нами шестиугольников может быть получен из
правильного поворотами треугольников OCD и OEF.
Пусть Qў и Rў -
середины сторон DEў и AFў
(рис. 18.3). При
повороте на 60° вектор
переходит в вектор
. Так как
и
, то вектор
переходит в вектор
при этом повороте. По предположению треугольник PQR правильный, т. е.
вектор
переходит в вектор
®
PR при повороте на 60°. Поэтому вектор
переходит в вектор
при повороте на 60°,
т. е. треугольник PQўRў правильный.
-
18.25.
-
Пусть K, L, M и N - вершины правильных треугольников,
построенных на сторонах BC, AB, AF и FE; B1, A1 и F1
- середины отрезков KL, LM и MN (рис. 18.4). Пусть, далее,
,
и
;
R - поворот на 60°, переводящий вектор
в
. Тогда
и
.
Поэтому
и
, т. е.
.
-
18.26.
-
Пусть при повороте на угол a с центром в центре
окружности S, переводящем точку C в точку D, точка A переходит
в некоторую точку Aў.
Тогда Р(BD, DAў) = a, т. е. точка D
лежит на окружности, из которой отрезок AўB виден под углом a.
-
18.27.
-
Пусть P - точка пересечения прямых l1 и l2. Тогда
Р(OA1, A1P) = Р(OA1, l1) = Р(OA2, l2) = Р(OA2, A2P). Поэтому точки O, A1, A2 и P лежат на
одной окружности.
-
18.28.
-
Одинаковые буквы G можно совместить поворотом с некоторым центром O
(если они совмещаются параллельным переносом, то AAi||AўAiў).
Согласно задаче 18.27 точка Xi лежит на описанной окружности
треугольника AўOA. Ясно, что точки, лежащие на одной окружности, образуют
выпуклый многоугольник.
-
18.29.
-
Пусть O - центр поворота R, переводящего отрезок
A(t1) A(t2) в отрезок B(t1) B(t2), где t1 и t2 -
некоторые моменты времени. Тогда этот поворот переводит A(t) в B(t)
в любой момент времени t. Поэтому, согласно задаче 18.27, точка O
лежит на описанной окружности треугольника APB.
-
18.30.
-
Пусть A и B - точки окружности с центром O, A1
и B1 - образы этих точек при повороте на угол a относительно
центра O; P и P1 - середины отрезков AB и A1B1;
M - точка пересечения прямых AB и A1B1. Прямоугольные
треугольники POM и P1OM имеют общую гипотенузу и равные катеты
PO = P1O, поэтому эти треугольники равны и РMOP = РMOP1 = a/2. Точка M получается из точки P поворотом на угол a/2 и
последующей гомотетией с коэффициентом 1/cos (a/2) и центром O.
Точки пересечения прямых AB и A1B1, AC и A1C1, BC и B1C1
являются вершинами треугольника, гомотетичного с коэффициентом
1/cos (a/2) треугольнику, образованному серединами сторон треугольника
ABC. Ясно, что треугольник, образованный серединами сторон
треугольника ABC, подобен треугольнику ABC.
-
18.31.
-
Согласно задаче 5.52 прямая, делящая пополам площадь
и периметр треугольника, проходит через центр его вписанной
окружности. Ясно также, что если прямая проходит через центр
вписанной окружности треугольника и делит его периметр пополам,
то она делит пополам и его площадь. Поэтому нужно провести
прямую, проходящую через центр вписанной окружности треугольника и
делящую его периметр пополам.
Предположим, что мы построили точки M и N на сторонах
AB и AC треугольника ABC так, что прямая MN проходит через
центр O вписанной окружности и делит периметр треугольника
пополам. Построим на луче AC точку D так, что AD = p, где p -
полупериметр треугольника ABC. Тогда AM = ND. Пусть Q -
центр поворота R, переводящего отрезок AM в отрезок DN (точку A
- в D, точку M - в N). Так как угол между прямыми AM и CN
известен, точку Q можно построить: она является вершиной равнобедренного
треугольника AQD, причем РAQD = 180° – РA и точки B
и Q лежат по одну сторону от прямой AD. При повороте R
отрезок OM переходит в отрезок OўN. Точку Oў мы можем построить.
Ясно, что РONOў = РA, поскольку угол между прямыми
OM и OўN равен РA. Поэтому точка N является точкой
пересечения прямой AC и дуги окружности, из которой отрезок OOў
виден под углом РA. Построив точку N, проводим прямую ON
и находим точку M.
Легко проверить, что если построенные точки M и N лежат
на сторонах AB и AC, то MN - искомая прямая. Основной момент
в доказательстве - доказательство того, что при повороте относительно
точки Q на 180° – РA точка M переходит в точку N.
Для доказательства этого факта надо воспользоваться тем, что РONOў = РA, т. е. при этом повороте прямая OM переходит в прямую OўN.
-
18.32.
-
Предположим, что k-угольники C1јCk и D1јDk
правильные одинаково ориентированные. Пусть C и D - центры этих
k-угольников,
и
.
Тогда
|
®
CiDi
|
= |
®
CiC
|
+ |
®
CD
|
+ |
®
DDi
|
= – ci + |
®
CD
|
+ di
|
. Вектор
переходит в вектор
при повороте Rj, где j - угол при вершине
правильного n-угольника. Поэтому
|
®
XBi
|
= |
®
XC
|
+ ci + |
®
CiBi
|
= |
®
XC
|
+ ci + Rj( – ci + |
®
CD
|
+ di)
|
.
Точку X подберем так, что
.
Тогда
|
®
XBi
|
= ci + Rj(di – ci) = Riyu
|
,
где u = ck + Rj(dk – ck), Ry -
поворот, переводящий вектор ck в c1. Следовательно,
B1јBk - правильный k-угольник с центром X. Аналогично
доказывается, что A1јAk - правильный k-угольник.
Обратное утверждение доказывается аналогично.
-
18.33.
-
Пусть H - точка пересечения высот треугольника ABC,
H1, H2 и H3 - точки, симметричные точке H относительно
сторон BC, CA и AB. Точки H1, H2 и H3 лежат на описанной
окружности треугольника ABC (задача 5.10). Пусть l - прямая,
проходящая через точку H. Прямая, симметричная прямой l относительно
стороны BC (соответственно CA и AB), пересекает описанную окружность
в точке H1 (соответственно H2 и H3) и в некоторой точке P1
(соответственно P2 и P3).
Рассмотрим какую¯нибудь другую прямую lў, проходящую через H.
Пусть j - угол между l и lў. Построим для прямой lў
точки P1ў, P2ў и P3ў тем же способом, каким были построены
для прямой l точки P1, P2 и P3. Тогда РPiHiPiў = j,
т. е. величина дуги PiPiў равна 2j (поворот от Pi и Piў
противоположен по направлению повороту от l и lў). Поэтому
точки P1ў, P2ў и P3ў являются образами точек P1, P2
и P3 при некотором повороте. Ясно, что если в качестве lў выбрать
высоту треугольника, опущенную из вершины A, то P1ў = P2ў = P3ў = A,
а значит, P1 = P2 = P3.
-
18.34.
-
Предположим, что лев бежал по ломаной A1A2јAn.
Распрямим траекторию движения льва следующим образом. Повернем
относительно точки A2 арену
цирка и дальнейшую траекторию так,
чтобы точка A3 попала на луч A1A2. Затем повернем относительно
точки A3 арену цирка и дальнейшую траекторию так, чтобы точка A4
попала на луч A1A2 и т. д. Центр O арены цирка переходит при
этом последовательно в точки O1 = O, O2, ј, On – 1;
точки A1, ј, An переходят в точки A1ў, ј, Anў,
лежащие на одной прямой (рис. 18.5).
Пусть ai – 1 -
угол поворота льва в точке Aiў. Тогда
РOi – 1AiўOi = ai – 1 и AiўOi – 1 = AiўOi Ј 10,
поэтому OiOi – 1 Ј 10ai – 1. Следовательно, 30 000 = A1ўAnў Ј A1ўO1 + O1O2 + ј + On – 2On – 1 + On – 1Anў Ј 10 + 10(a1 + ј + an – 2) + 10, т. е. a1 + ј + an – 2 і 2998.
-
18.35.
-
Рассмотрим композицию поворотов RBb°RAa. Если A = B,
то утверждение задачи очевидно, поэтому будем считать, что A № B.
Пусть l = AB, прямые a и b проходят через точки A и B
соответственно, причем Р(a, l) = a/2 и Р(l, b) = b/2.
Тогда RBb°RAa = Sb°Sl°Sl°Sa = Sb°Sa.
Если a||b, то Sa°Sb = T2u, где Tu -
параллельный перенос, переводящий a в b, причем u^a.
А если прямые a и b не параллельны и O - точка их пересечения,
то Sa°Sb - поворот на угол a + b с центром O. Ясно
также, что a||b тогда и только тогда, когда (a/2) + (b/2) = kp,
т. е. a + b
= 2kp.
-
18.36.
-
Пусть P, Q, R и S - центры квадратов, построенных
внешним образом на сторонах AB, BC, CD и DA соответственно.
Построим на отрезках QR и SP внутренним образом равнобедренные
прямоугольные треугольники с вершинами O1 и O2. Тогда
D = RR90°°RQ90°(B) = RO1180°(B)
и B = RP90°°RS90°(D) = RO2180°(D),
т. е. O1 = O2 - середина отрезка BD.
При повороте на 90° относительно точки O = O1 = O2, переводящем
точку Q в R, точка S переходит в P, т. е. отрезок QS
переходит в RP, а значит, эти отрезки равны и перпендикулярны.
-
18.37.
-
Пусть P, Q, R и S - центры квадратов, построенных
внешним образом на сторонах AB, BC, CD и DA параллелограмма
ABCD. Согласно предыдущей задаче PR = QS и PR^QS. Кроме
того, центр симметрии параллелограмма ABCD является центром
симметрии четырехугольника PQRS, т. е. PQRS - параллелограмм
с равными и перпендикулярными диагоналями, а значит, он квадрат.
-
18.38.
-
Пусть P, Q и R - центры квадратов, построенных внешним
образом на сторонах AB, BC и CA. Рассмотрим поворот на 90°
с центром R, переводящий C в A. При повороте на 90° в том
же направлении с центром P точка A переходит в B. Композиция
этих двух поворотов является поворотом на 180°, поэтому центр
этого поворота - середина отрезка BC. С другой стороны, центр
этого поворота является вершиной равнобедренного прямоугольного
треугольника с основанием PR, т. е. является центром квадрата,
построенного на PR. Этот квадрат построен на стороне треугольника
PQR именно внутренним образом.
-
18.39.
-
Если O1 = O3,
то RD90°°RC90°°RB90°°RA90° = RO3180°°RO1180° = E.
Поэтому E = RA90°°E°RA – 90° = RA90°°RD90°°RC90°°RB90° = RO4180°°RO2180°,
т. е. O4 = O2.
(E - тождественное
преобразование.)
-
18.40.
-
а) См. решение более общей задачи 18.44 (достаточно
положить a
= b
= g
= 120°). В случае б) доказательство
аналогично.
в) Пусть Q и R (соответственно Q1 и R1) - центры правильных
треугольников, построенных внешним (соответственно внутренним)
образом на сторонах AC и AB. Так как AQ = b/Ц3, AR = c/Ц3
и РQAR = 60° + a, то 3QR2 = b2 + c2 – 2bccos (a + 60°).
Аналогично 3Q1R12 = b2 + c2 – 2bccos (a – 60°). Поэтому
разность площадей полученных правильных треугольников равна
(QR2 – Q1R12)Ц3/4 = bcsin asin 60°/Ц3 = SABC.
-
18.41.
-
Композиция поворота на 60° относительно точки Aў,
переводящего B в C, поворота на 60° относительно точки Bў,
переводящего C в A, и поворота на 120° относительно
точки M, переводящего A в B, имеет неподвижную точку B. Так как
первые два поворота производятся в направлении, противоположном
направлению последнего поворота, то композиция этих поворотов является
параллельным переносом, имеющим неподвижную точку, т. е. является
тождественным преобразованием: RM – 120°°RBў60°°RAў60° = E. Поэтому RBў60°°RAў60° = RM120°, т. е. точка M является центром
поворота RBў60°°RAў60°. Следовательно,
РMAўBў = РMBўAў = 30°, т. е. AўBўM -
равнобедренный треугольник, причем РAўMBў = 120°.
-
18.42.
-
Из условия задачи следует, что RC – 2g = RB2b°RA2a,
т. е. точка C является центром композиции поворотов RB2b°RA2a. Это означает, что РBAC = a и РABC = b
(см. задачу 18.35). Поэтому РACB = p – a – b
= g.
-
18.43.
-
Обозначим данные точки через M1, ј, Mn. Предположим.
что мы построили многоугольник A1A2јAn так, что треугольники
A1M1A2, A2M2A3, …, AnMnA1 равнобедренные, причем
РAiMiAi + 1 = ai и стороны многоугольника являются
основаниями этих равнобедренных треугольников.
Ясно, что RMnan°ј°RM1a1(A1) = A1.
Если a1 + ј + an № k · 360°,
то точка A1
является центром поворота
RMnan°ј°RM1a1.
Центр композиции
поворотов мы можем построить. Построение остальных вершин многоугольника
производится очевидным образом.
Если a1 + ј + an = k · 360°, то задача неопределенная: либо любая точка A1 задает
многоугольник, обладающий требуемым свойством, либо задача не имеет
решений.
-
18.44.
-
Так как RCўg°RBўb°RAўa(B) = RCўg°RBўb(C) = RCўg(A) = B, то B - неподвижная
точка композиции поворотов RCўg°RBўb°RAўa. А так как a + b + g
= 2p, то эта композиция является
параллельным переносом, имеющим неподвижную точку, т. е. тождественным
преобразованием. Остается воспользоваться результатом задачи 18.42.
-
18.45.
-
Так как RGўp – a°RAa(N) = L
и RGp – a°RAa(L) = N,
то преобразования RGўp – a°RAa
и RGp – a°RAa являются центральными симметриями
относительно середины отрезка LN, т. е. RGўp – a°RAa = RGp – a°RAa. Следовательно,
RGўp – a = RGp – a и Gў = G.
-
18.46.
-
Пусть A1, B1 и C1 - центры описанных окружностей
треугольников APR, BPQ и CQR. При последовательных поворотах
с центрами A1, B1 и C1 на углы 2a, 2b и 2g
точка R переходит сначала в P, затем в Q, а потом возвращается
на место. Так как 2a + 2b + 2g
= 360°, то композиция указанных
поворотов - тождественное преобразование. Следовательно, углы
треугольника A1B1C1 равны a, b и g (см. задачу 18.42).
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:46.

 Глава 18. Задачи для самостоятельного решения |
Глава 18. Задачи для самостоятельного решения | 

 Глава 18. Задачи для самостоятельного решения |
Глава 18. Задачи для самостоятельного решения | 
