Глава 1. § 1  |	Оглавление |	Глава 1. § 3

§ 2.  Отношение сторон подобных треугольников

1.17.

а) В треугольнике ABC проведена биссектриса BD внутреннего или внешнего угла. Докажите, что AD : DC  =  AB : BC.

б) Докажите, что центр O вписанной окружности треугольника ABC делит биссектрису AA₁ в отношении AO : OA₁  =  (b + с) : a, где a, b, c — длины сторон треугольника.

1.18.

Длины двух сторон треугольника равны a, а длина третьей стороны равна b. Вычислите радиус его описанной окружности.

1.19.

Прямая, проходящая через вершину A квадрата ABCD, пересекает сторону CD в точке E и прямую BC в точке F. Докажите, что

1 AE2

+

1 AF2

=

1 AB2

.

1.20.

На высотах BB₁ и CC₁ треугольника ABC взяты точки B₂ и C₂ так, что РAB₂C = РAC₂B = 90°. Докажите, что AB₂ = AC₂.

1.21.

В трапецию ABCD (BC||AD) вписана окружность, касающаяся боковых сторон AB и CD в точках K и L соответственно, а оснований AD и BC в точках M и N.

а) Пусть Q — точка пересечения отрезков BM и AN. Докажите, что KQ||AD.

б) Докажите, что AK · KB = CL · LD.

1.22.

На стороны BC и CD параллелограмма ABCD (или на их продолжение) опущены перпендикуляры AM и AN. Докажите, что DMAN ~ DABC.

1.23.

Прямая l пересекает стороны AB и AD параллелограмма ABCD в точках E и F соответственно. Пусть G — точка пересечения прямой l с диагональю AC. Докажите, что

AB AE

+

AD AF

=

AC AG

.

1.24.

Пусть AC — бóльшая из диагоналей параллелограмма ABCD. Из точки C на продолжения сторон AB и AD опущены перпендикуляры CE и CF соответственно. Докажите, что AB · AE + AD · AF = AC².

1.25.

Углы треугольника ABC связаны соотношением 3a +  2b  =  180°. Докажите, что a²  +  bc = c².

1.26.

Концы отрезков AB и CD перемещаются по сторонам данного угла, причем прямые AB и CD перемещаются параллельно; M — точка пересечения отрезков AB и CD. Докажите, что величина

AM · BM CM · DM

остается постоянной.

1.27.

Через произвольною точку P стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части.

1.28.

На биссектрисе угла с вершиной C взята точка P. Прямая, проходящая через точку P, высекает на сторонах угла отрезки длиной a и b. Докажите, что величина

1 a

+

1 b

не зависит от выбора этой прямой.

1.29.

На стороне BC равностороннего треугольника ABC как на диаметре внешним образом построена полуокружность, на которой взяты точки K и L, делящие полуокружность на три равные дуги. Докажите, что прямые AK и AL делят отрезок BC на равные части.

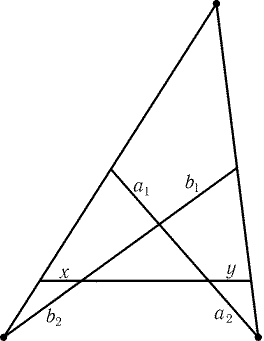
Рис. 1.1

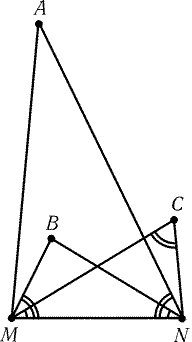
Рис. 1.2

1.30. Точка O — центр вписанной окружности треугольника ABC. На сторонах AC и BC выбраны точки M и K соответственно так, что BK · AB = BO² и AM · AB = AO². Докажите, что точки M, O и K лежат на одной прямой.

1.31^*. Докажите,  что  если  a₁ = a₂ и b₁ = b₂ (рис. 1.1), то x = y.

1.32^*. На отрезке MN построены подобные, одинаково ориентированные треугольники AMN, NBM и MNC (рис. 1.2). Докажите, что треугольник ABC подобен всем
этим треугольникам, а центр его описанной окружности равноудален от точек M и N.

1.33^*. Отрезок  BE  разбивает  треугольник ABC на два подобных треугольника, причем коэффициент подобия равен Ц3. Найдите углы треугольника ABC.

Глава 1. § 1  |	Оглавление |	Глава 1. § 3

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.