Глава 21. § -1  |	Оглавление |	Глава 22.

21.1.

Возьмем три вертикальные прямые и девять горизонтальных. Будем рассматривать только точки пересечения этих прямых. Так как имеется лишь 2³ = 8 вариантов раскраски трех точек в два цвета, то найдутся две горизонтальные прямые, на которых лежат одинаково раскрашенные тройки точек. Среди трех точек, раскрашенных в два цвета, найдутся две одинаково раскрашенные точки. Вертикальные прямые, проходящие через эти точки, вместе с ранее выбранными двумя горизонтальными являются искомыми.

21.2.

Средние линии правильного треугольника со стороной 1 разбивают его на четыре правильных треугольника со стороной 0,5. Поэтому в одном из них лежат по крайней мере две данные точки, причем эти точки не могут попасть в вершины треугольника. Расстояние между этими точками меньше 0,5.

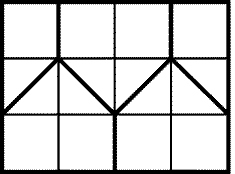
Рис. 21.2

21.3. Разрежем прямоугольник на пять фигур, как показано на рис. 21.2. В одну из них попадут по крайней мере две точки, а расстояние между любыми двумя точками каждой из этих фигур не превосходит Ц5.

21.4. К краю шахматной доски 8×8 прилегает 28 полей. Проведем 28 отрезков, соединяющих центры соседних крайних полей. Каждая прямая может пересекать не более двух таких отрезков, поэтому 13 прямых могут пересекать не более 26 отрезков, т. е. найдутся по крайней мере 2 отрезка, не пересекающихся ни с одной из 13 проведенных прямых. Поэтому тринадцатью прямыми нельзя разбить шахматную доску так, чтобы в каждой части лежало не более одной отмеченной точки, поскольку оба конца отрезка, не пересекающегося с прямыми, лежат в одной части.

21.5.

Пусть A - одна из данных точек. Если все остальные точки лежат в круге S₁ радиуса 1 с центром A, то доказывать больше нечего. Пусть теперь B - данная точка, лежащая вне круга S₁, т. е. AB > 1. Рассмотрим круг S₂ радиуса 1 с  центром B. Среди точек A, B и C, где C - любая из данных точек, найдутся две на расстоянии меньше 1, причем это не могут быть точки A и B. Поэтому круги S₁ и S₂ содержат все данные точки, т. е. один из них содержит не менее 13 точек.

21.6.

Разрежем данный квадрат на 25 одинаковых квадратиков со стороной 0,2. В один из них попадает не меньше трех точек. Радиус описанной окружности квадрата со стороной 0,2 равен 1/5Ц2 < 1/7, поэтому его можно накрыть кругом радиуса 1/7.

21.7.

Возьмем 1985 дисков, раскрашенных так же, как второй из наших дисков, и положим их на первый диск так, чтобы они занимали все возможные положения. Тогда над каждым окрашенным сектором первого диска расположено 200 окрашенных секторов, т. е. всего имеется 200² пар совпадающих окрашенных секторов. Пусть имеется n положений второго диска, при которых совпадает не менее 21 пары окрашенных секторов. Тогда число совпадений окрашенных секторов не меньше 21n. Поэтому 21n Ј 200², т. е. n Ј 1904,8. Так как n - целое число, то n Ј 1904. Следовательно, по крайней мере при 1985 – 1904 = 81 положениях совпадает не более 20 пар окрашенных секторов.

21.8.

Данные прямые не могут пересекать соседние стороны квадрата ABCD, так как иначе образуются не два четырехугольника, а треугольник и пятиугольник. Пусть прямая пересекает стороны BC и AD в точках M и N. Трапеции ABMN и CDNM имеют равные высоты, поэтому их площади относятся как средние линии, т. е. MN делит отрезок, соединяющий середины сторон AB и CD, в отношении 2 : 3. Точек, делящих средние линии квадрата в  отношении 2 : 3, имеется ровно четыре. Так как данные девять прямых проходят через эти четыре точки, то через одну из точек проходят по крайней мере три прямые.

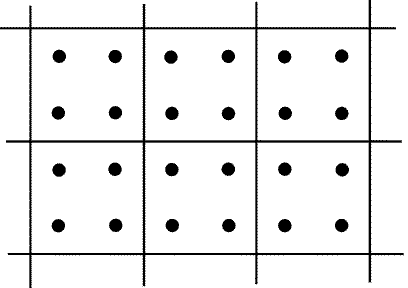
Рис. 21.3

21.9. Разобьем деревья на 2500 четверок, как показано на рис. 21.3. В каждой такой четверке нельзя срубить более одного дерева. С другой стороны, можно срубить все деревья, растущие в левых верхних углах квадратов, образованных нашими четверками деревьев. Поэтому наибольшее число деревьев, которые можно срубить, равно 2500.

21.10. Так как диагонали, выходящие из одной вершины, делят n-угольник на n – 2 треугольника, n – 2 точки необходимы.

Из рис. 21.4 можно понять, как обойтись n – 2 точками: достаточно отметить по одной точке в каждом зачерненном треугольнике. В самом деле, внутри треугольника A_pA_qA_r, где p < q < r, всегда содержится зачерненный треугольник, прилегающий к вершине A_q.

Рис. 21.4

21.11. Возможны два случая:

1. Точка P лежит на некоторой диагонали AB. Тогда прямые PA и PB совпадают и не пересекают сторон. Остаются 2n – 2 прямые; они пересекают не более 2n – 2 сторон.

2. Точка P не лежит на диагонали многоугольника A₁A₂јA_2n. Проведем диагональ A₁A_n + 1. По обе стороны от нее лежит по n сторон. Пусть для определенности точка P лежит внутри многоугольника A₁јA_n + 1 (рис. 21.5). Тогда прямые PA_n + 1, PA_n + 2, ј, PA_2n, PA₁ (число этих прямых равно n + 1) не могут пересекать стороны A_n + 1A_n + 2, A_n + 2A_n + 3, ј, A_2nA₁. Поэтому оставшиеся прямые могут пересекать не более чем n – 1 из этих n сторон.

21.12.

Количество диагоналей 2n-угольника равно 2n(2n – 3)/2 = n(2n – 3). Легко проверить, что диагоналей, параллельных данной стороне, не более n – 2. Поэтому всего диагоналей, параллельных сторонам, не более 2n(n – 2). А так как 2n(n – 2) < n(2n – 3), то найдется диагональ, не параллельная ни одной из сторон.

21.13.

Предположим, что нет равнобедренного прямоугольного треугольника с катетами, параллельными сторонами клеток, и вершинами одного цвета. Для удобства можно считать, что раскрашены не узлы, а клетки. Разобьем лист на квадраты со стороной 4; тогда на диагонали каждого такого квадрата найдутся две клетки одного цвета. Пусть число n больше количества различных раскрасок квадрата со стороной 4. Рассмотрим квадрат, состоящий из n² квадратов со стороной 4. На его диагонали найдутся два одинаково раскрашенных квадрата со стороной 4. Возьмем, наконец, квадрат K, на диагонали которого найдутся два одинаково раскрашенных квадрата со стороной 4n.

Рис. 21.5 Рис. 21.6

21.14.

Возьмем на плоскости произвольную точку и проведем через нее прямые, параллельные данным. Они разделят плоскость на 2n углов, в сумме дающих 360°. Поэтому один из этих углов не превосходит 180°/n.

21.15.

Предположим, что сумма длин хорд не меньше pk, и докажем, что тогда найдется диаметр, пересекающий по крайней мере k + 1 хорду. Так как длина дуги, стягиваемой хордой, больше длины этой хорды, то сумма длин дуг, стягиваемых данными хордами, больше pk. Если мы к этим дугам добавим еще и дуги, симметричные им относительно центра окружности, то сумма длин всех рассматриваемых дуг будет больше 2pk. Поэтому найдется точка, которую покрывает по крайней мере k + 1 из этих дуг. Диаметр, проведенный через эту точку, пересекает по крайней мере k + 1 хорду.

21.16.

а) Можно. Пусть O - центр правильного пятиугольника ABCDE. Тогда круги, вписанные в углы AOC, BOD, COE, DOA и EOB, обладают требуемым свойством.

21.17.

Пусть l₁ - произвольная прямая, перпендикулярная l. Обозначим длины проекций i-го отрезка на прямые l и l₁ через a_i и b_i соответственно. Так как длина каждого отрезка равна 1, то a_i + b_i і 1. Поэтому (a₁ + ј + a_4n) + (b₁ + ј + b_4n) і 4n. Пусть для определенности a₁ + ј + a_4n і b₁ + ј + b_4n. Тогда a₁ + ј + a_4n і 2n. Все данные отрезки проецируются на отрезок длиной 2n, так как они лежат внутри окружности радиуса n. Если бы проекции данных отрезков на прямую l не имели общих точек, то выполнялось бы неравенство a₁ + ј + a_4n < 2n. Поэтому на l есть точка, в которую проецируются точки по крайней мере двух данных отрезков. Перпендикуляр к l, проведенный через эту точку, пересекает по крайней мере два данных отрезка.

21.18.

Спроецируем все данные окружности на сторону AB квадрата ABCD. Проекцией окружности длиной l является отрезок длиной l/p. Поэтому сумма длин проекций всех данных окружностей равна 10/p. Так как 10/p > 3 = 3AB, то на отрезке AB есть точка, принадлежащая проекциям по крайней мере четырех окружностей. Перпендикуляр к AB, проведенный через эту точку, пересекает по крайней мере четыре окружности.

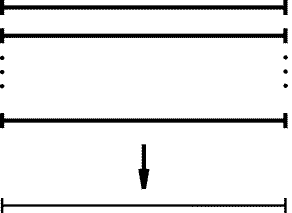
Рис. 21.7

21.19. Разрежем отрезок на десять отрезков длиной 0,1, сложим их стопочкой и спроецируем на такой же отрезок (рис. 21.7). Так как расстояние между любыми двумя окрашенными точками не равно 0,1, то окрашенные точки соседних отрезков не могут проецироваться в одну точку. Поэтому ни в одну точку не могут проецироваться окрашенные точки более чем пяти отрезков. Следовательно, сумма длин проекций окрашенных отрезков (равная сумме их длин) не превосходит 5 · 0,1 = 0,5.

21.20. Совместим данные окружности и посадим в фиксированную точку одной из них маляра. Будем вращать эту окружность и поручим маляру красить ту точку окружности, мимо которой он проезжает, всякий раз, когда какая-либо отмеченная точка лежит на отмеченной дуге. Нужно доказать, что после полного оборота часть окружности останется неокрашенной. Конечный результат работы маляра будет такой же, как если бы ему поручили на i-м обороте красить окружность, когда i-я отмеченная точка лежит на одной из отмеченных дуг, и сделали бы 100 оборотов. Так как в этом случае при каждом обороте окрашивается меньше 1 см, после 100 оборотов будет окрашено меньше 100 см. Поэтому часть окружности останется неокрашенной.

21.21.

Совместим данные окружности и посадим в фиксированную точку одной из них маляра. Будем вращать эту окружность и поручим маляру красить ту точку окружности, мимо которой он проезжает, всякий раз, когда пересекаются какие-либо отмеченные дуги. Нужно доказать, что после полного оборота часть окружности останется неокрашенной. Конечный результат работы маляра будет такой же, как если бы ему поручили на i-м обороте красить окружность, когда i-я отмеченная дуга окружности, на которой сидит маляр, пересекается с  какой-либо отмеченной дугой другой окружности, и сделали бы k оборотов.

21.22.

Рассмотрим фигуру, состоящую из всех точек, удаленных от квадратика со стороной 1 на расстояние не больше 1 (рис. 21.8). Ясно, что круг радиуса 1, центр которого расположен вне этой фигуры, не пересекается с квадратиком. Площадь такой фигуры равна p + 5. Центр нужного круга должен также находиться на расстоянии больше 1 от сторон большого квадрата, т. е. внутри квадрата со стороной 13. Ясно, что 20 фигур площадью p + 5 не могут покрыть квадрат со стороной 13, так как 20(p + 5) < 13². Круг с центром в непокрытой точке обладает требуемым свойством.

21.23.

Приклеим фигуру к клетчатой бумаге произвольным образом, разрежем бумагу по клеткам и сложим их в стопку, перенося их параллельно и не переворачивая. Спроецируем эту стопку на клетку. Проекции частей фигуры не могут покрыть всю клетку, так как их площадь меньше. Вспомним теперь, как была расположена фигура на клетчатой бумаге, и сдвинем клетчатую бумагу параллельно, чтобы ее вершины попали в точки, проецирующиеся в какую-либо непокрытую точку. В результате получим искомое расположение фигуры.

Рис. 21.8 Рис. 21.9

21.24.

Для каждого креста рассмотрим круг радиусом 1/2Ц2 с центром в центре креста. Докажем, что если пересекаются два таких круга, то пересекаются и сами кресты. Расстояние между центрами пересекающихся равных кругов не превосходит их удвоенного радиуса, поэтому расстояние между центрами соответствующих им крестов не превосходит 1/Ц2. Рассмотрим прямоугольник. заданный перекладинами первого креста и центром второго (рис. 21.9). Одна из перекладин второго креста проходит через этот прямоугольник, поэтому она пересекает первый крест, так как длина перекладины равна 1/Ц2, а длина диагонали прямоугольника не превосходит 1/Ц2. В круге конечного радиуса можно разместить лишь конечное число непересекающихся кругов радиуса 1/2Ц2.

21.25.

Пусть F - данная фигура, S₁, ј, S_n - круги радиуса 1 с центрами в точках A₁, ј, A_n. Так как круги S₁, ј, S_n попарно не пересекаются, то фигуры V_i = FЗS_i попарно не пересекаются, а значит, сумма их площадей не превосходит площади фигуры F, т. е. она меньше p. Пусть O - произвольная точка и W_i - образ фигуры V_i при переносе на вектор

® AiO

. Фигуры W_i лежат внутри круга S радиуса 1 с центром O и сумма их площадей меньше площади этого круга. Поэтому некоторая точка B круга S не принадлежит ни одной из фигур W_i. Ясно, что перенос на вектор

® BO

искомый.

21.26.

Заметим сначала, что точка X принадлежит кольцу с центром O тогда и только тогда, когда точка O принадлежит такому же кольцу с центром X. Поэтому достаточно доказать, что если построить кольца с центрами в данных точках, то одну из точек рассматриваемого круга покроет не менее 10 колец. Рассматриваемые кольца лежат внутри круга радиуса 16 + 3 = 19, площадь которого равна 361p. Остается заметить, что 9 · 361p  =  3249p, а суммарная площадь колец равна 650 · 5p  =  3250p.

21.27.

а) Пусть C_n^k - число способов выбрать k элементов из n. Можно проверить, что

(x + y)n =

n е k = 0

Cnk xk yn – k

(бином Ньютона).

Обозначим через W_m площадь части плоскости, покрытой ровно m фигурами. Эта часть состоит из кусков, каждый из которых покрыт какими-то определенными m фигурами. Площадь каждого такого куска при вычислении M_k учитывается C_m^k раз, так как из m фигур можно образовать C_m^k пересечений k фигур. Поэтому M_k = C_k^k W_k + C_k + 1^k W_k + 1 + ј + C_n^k W_n. Следовательно, M₁ – M₂ + M₃ – ј  =  C₁¹ W₁ + (C₂¹ – C₂²)W₂ + ј + (C_n¹ – C_n² + C_n³ – ј)W_n = W₁ + ј + W_n, так как C_m¹ – C_m² + C_m³ – ј – ( – 1)^m C_m^m = ( – 1 + C_m¹ – C_m² + ј) + 1 =  – (1 – 1)^m + 1 = 1. Остается заметить, что S = W₁ + ј + W_n.

б) Согласно задаче а)

S – (M1 – M2 + ј + ( – 1)m + 1Mm) = ( – 1)m + 2Mm + 1 + ( – 1)m + 3Mm + 2 + ј +

+ ( – 1)n + 1Mn =  n е i = 1  (( – 1)m + 2Cim + 1 + ј + ( – 1)n + 1Cin)Wi

(считается, что если k > i, то C_i^k = 0). Поэтому достаточно проверить, что C_i^m + 1 – C_i^m + 2 + C_i^m + 3 – ј + ( – 1)^{m + n + 1}C_iⁿ і 0 при i Ј n. Из тождества (x + y)ⁱ = (x + y)^i – 1(x + y) следует равенство C_i^j = C_i – 1^j – 1 + C_i – 1^j. Поэтому C_i^m + 1 – C_i^m + 2 + ј + ( – 1)^{m + n + 1}C_iⁿ = C_i – 1^m±C_i – 1ⁿ. Остается заметить, что C_i – 1ⁿ = 0 при i Ј n.

21.28.

а) Согласно задаче 21.27, а) 6 = 9 – (S₁₂ + S₂₃ + S₁₃) + S₁₂₃, т. е. S₁₂ + S₂₃ + S₁₃ = 3 + S₁₂₃ і 3. Поэтому одно из чисел S₁₂, S₂₃, S₁₃ не меньше 1.

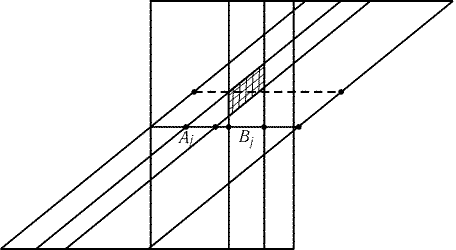
Рис. 21.10

21.29. Пусть площадь кафтана равна M, площадь пересечения заплат с номерами i₁, ј, i_k равна S_i1јik, а 

Mk =

е

Si1јik

. Согласно задаче 21.27, а) M – M₁ + M₂ – M₃ + M₄ – M₅ і 0, так как M і S. Аналогичные неравенства можно написать не только для всего кафтана, но и для каждой заплаты: если мы рассмотрим заплату S₁ как кафтан с заплатами S₁₂, S₁₃, S₁₄, S₁₅, то получим

S1 –

е

S1i +

е

S1ij –

е

S1ijk + S12345 і 0

. Сложив такие неравенства для всех пяти заплат, получаем M₁ – 2M₂ + 3M₃ – 4M₄ + 5M₅ і 0 (слагаемое S_i1јik входит в неравенства для заплат i₁, ј, i_k, поэтому в сумму всех неравенств оно входит с коэффициентом k). Складывая неравенства 3(M – M₁ + M₂ – M₃ + M₄ – M₅) і 0 и M₁ – 2M₂ + 3M₃ – 4M₄ + 5M₅ і 0, получаем неравенство 3M – 2M₁ + M₂ – M₄ + 2M₅ і 0. Прибавив к нему неравенство M₄ – 2M₅ і 0 (оно следует из того, что S₁₂₃₄₅ входит во все S_i1i2i3i4, т. е. M₄ і 5M₅ і 2M₅), получаем 3M – 2M₁ + M₂ і 0, т. е. M₂ і 2M₁ – 3M і 5 – 3 = 2.

Так как из пяти заплат можно образовать десять пар, площадь пересечения одной из этих пар не меньше M₂/10 і 0,2.

21.30. Пусть  – 1 Ј c Ј 1. Сдвинем данный отрезок на c вдоль себя, а затем сдвинем его на c в ортогональном направлении. Заштрихованная на рис. 21.10 область соответствует пересечению отрезков A_i и B_j. Ее площадь равна произведению длин этих отрезков. Если рассмотреть все пары отрезков систем A и B, то заштрихованная область будет иметь площадь p(1 – p). Поэтому некоторое горизонтальное сечение заштрихованных областей имеет длину не меньше p(1 – p)/2.

Замечание. Если вместо отрезка рассматривать окружность (и вместо параллельного переноса поворот), то p(1 – p)/2 можно заменить на p(1 – p).

Глава 21. § -1  |	Оглавление |	Глава 22.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.