Глава 23. § 4  |	Оглавление |	Глава 23. § 6

§ 5.  Другие вспомогательные раскраски

23.26.

Правильный треугольник разбит на n² одинаковых правильных треугольников (рис. 23.4). Часть из них занумерована чис-

лами 1, 2, ј, m, причем треугольники с последовательными номерами имеют смежные стороны. Докажите, что m Ј n² – n + 1.

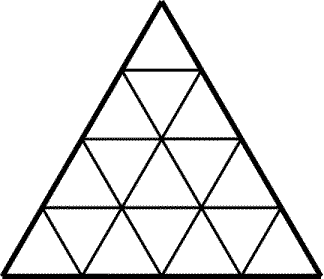
Рис. 23.4

23.27. Дно прямоугольной коробки выложено плитками размером 2×2 и 1×4. Плитки высыпали из коробки и потеряли одну плитку 2×2. Вместо нее достали плитку 1×4. Докажите, что выложить дно коробки плитками теперь не удастся.

23.28.                        Из  листа  клетчатой  бумаги размером 29×29 клеток вырезано 99 квадратиков размером 2×2 клетки. Докажите, что из него можно вырезать еще один такой квадратик.

23.29. Выпуклый n-угольник разбит на треугольники непересекающимися диагоналями, причем в каждой его вершине сходится нечетное число треугольников. Докажите, что n делится на 3.

*       *      *

23.30. Можно ли шашечную доску размером 10×10 замостить плитками размером 1×4?

23.31.

На клетчатой бумаге даны произвольные n клеток. Докажите, что из них можно выбрать не менее n/4 клеток, не имеющих общих точек.

23.32^*.

Докажите, что если вершины выпуклого n-угольника лежат в узлах клетчатой бумаги, а внутри и на его сторонах других узлов нет, то n Ј 4.

23.33^*.

Из 16 плиток размером 1×3 и одной плитки 1×1 сложили квадрат со стороной 7. Докажите, что плитка 1×1 лежит в центре квадрата или примыкает к его границе.

23.34^*.

Картинная галерея представляет собой невыпуклый n-угольник. Докажите, что для обзора всей галереи достаточно [n/3] сторожей.

Глава 23. § 4  |	Оглавление |	Глава 23. § 6

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.