| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
23.1.
-
а) Пусть прямая пересекает все стороны многоугольника.
Рассмотрим все вершины, лежащие по одну сторону от нее. Каждой
из этих вершин можно поставить в соответствие пару сторон, из
нее выходящих. При этом получим разбиение всех сторон многоугольника
на пары. Поэтому если прямая пересекает все стороны
m-угольника, то m четно.
б) Из рис. 23.5 видно, как построить 2n-угольник и прямую,
пересекающую все его стороны, при любом n.
-
23.2.
-
Прямая l задает две полуплоскости; одну из них будем
называть верхней, а другую нижней. Пусть n1 (соответственно n2)
- число вершин ломаной, лежащих на прямой l, для которых
оба выходящих из них звена лежат в верхней (соответственно
в нижней) полуплоскости, а m - число всех остальных точек
пересечения прямой l и ломаной. Совершим обход ломаной, выйдя из
некоторой точки, не лежащей на прямой l, и вернувшись в ту же
точку. При этом мы переходим из одной полуплоскости в другую,
только проходя через любую из m точек пересечения. Так как мы
вернемся в ту же точку, из которой начали обход, то m четно.
По условию n1 + n2 + m = 1985, поэтому число n1 + n2 нечетно, т. е.
n1 № n2. Пусть для определенности n1 > n2. Проведем тогда в
верхней полуплоскости прямую l1, параллельную l и удаленную
от нее на расстояние меньшее, чем любое ненулевое расстояние от l
до вершин ломаной (рис. 23.6). Число точек пересечения ломаной с
прямой l1 равно 2n1 + m > n1 + n2 + m = 1985, т. е. l1 -
искомая прямая.
-
23.3.
-
Нет, не могут. После каждого удара изменяется ориентация
(т. е. направление обхода) треугольника ABC.
-
23.4.
-
Пусть на клетчатой бумаге окрашено несколько клеток
и nk - число окрашенных клеток, имеющих ровно k окрашенных
соседей. Пусть N - число общих сторон окрашенных клеток. Так
как каждая из них принадлежит ровно двум окрашенным клеткам,
то N = (n1 + 2n2 + 3n3 + 4n4)/2 = (n1 + n3)/2 + n2 + n3 + 2n4. Поскольку N
- целое число, то число n1 + n3 четно.
Мы доказали, что число окрашенных клеток, имеющих нечетное
число окрашенных соседей, всегда четно. Поэтому нельзя окрасить 25
клеток так, чтобы у каждой из них было нечетное число
окрашенных соседей.
Рис. 23.7
23.5.
Предположим, что окружность разбита на дуги указанным
образом, причем диаметрально противоположных точек деления нет.
Тогда против концов любой дуги длиной 1 не лежат точки разбиения,
поэтому против нее лежит дуга длиной 3. Выбросим одну из дуг
длиной 1 и противолежащую ей дугу длиной 3. При этом окружность
разбивается на две дуги. Если на одной из них лежит m дуг
длиной 1 и n дуг длиной 3, то на другой лежит m дуг длиной 3
и n дуг длиной 1. Общее количество дуг длиной 1 и 3, лежащих
на этих двух «больших» дугах, равно 2(k – 1), поэтому n + m = k – 1.
Так как, кроме дуг длиной 1 и 3, есть дуги только с четной
длиной, то четность длины каждой из двух рассматриваемых дуг
совпадает с четностью числа k – 1. С другой стороны, длина каждой
из них равна (6k – 1 – 3)/2 = 3k – 2. Получено противоречие, так как
числа k – 1 и 3k – 2 имеют разную четность.
23.6.
Возьмем соседние звенья AB и BC и назовем уголком угол,
симметричный углу ABC относительно точки B (на рис. 23.7 уголок
заштрихован). Такие же уголки можно рассмотреть для всех вершин ломаной.
Ясно, что число особых пар равно числу точек пересечения звеньев с
уголками. Остается заметить, что число звеньев ломаной, пересекающихся
с одним уголком, четно, так как по пути от A к C ломаная
входит в уголок столько же раз, сколько выходит из него.
-
23.7.
-
Рассмотрим отрезки, на которые разбита сторона 01. Пусть a -
число отрезков вида 00, b - число отрезков вида 01. Для каждого
отрезка рассмотрим число нулей, стоящих на его концах, и сложим
все эти числа. В итоге получим 2a + b. С другой стороны, все
«внутренние» нули входят в эту сумму дважды, а есть еще один
нуль, стоящий в вершине исходного треугольника. Поэтому число
2a + b нечетно, т. е. b нечетно.
Перейдем теперь к разбиению треугольника. Пусть a1 - общее
количество треугольников вида 001 и 011, а b1 - число
треугольников вида 012. Для каждого треугольника рассмотрим число его
сторон вида 01 и сложим все эти числа. В итоге получим 2a1 + b1. С
другой стороны, все «внутренние» стороны входят в эту сумму дважды,
а все «граничные» лежат на стороне 01 исходного треугольника
и число их нечетно по предыдущему рассуждению. Поэтому число
2a1 + b1 нечетно, в частности, b1 № 0.
-
23.8.
-
Предположим, что все пары вершин задают отрезки разной
длины. Отрезку ApAq поставим в соответствие наименьшее из чисел
|p – q| и 2n – |p – q|. В результате для данных n пар вершин получим
числа 1, 2, ј, n; пусть среди этих чисел k четных и n – k
нечетных. Нечетным числам соответствуют отрезки ApAq, где числа p
и q разной четности. Поэтому среди вершин остальных отрезков будет k
вершин с четными номерами и k вершин с нечетными номерами, причем
отрезки соединяют вершины с номерами одной четности. Следовательно,
число k четно. Для чисел n вида 4m, 4m + 1, 4m + 2 и 4m + 3
количество k четных чисел равно 2m, 2m, 2m + 1 и 2m + 1
соответственно, поэтому n = 4m или n = 4m + 1.
-
23.9.
-
Предположим, что мы разбили десятиугольник требуемым
образом. Пусть n - число сторон черных треугольников, m -
число сторон белых треугольников. Так как каждая сторона черного
треугольника (кроме сторон многоугольника) является также и стороной
белого треугольника, то n – m = 10. С другой стороны, оба
числа n и m делятся на 3. Получено противоречие.
-
23.10.
-
Пусть Q - квадратный лист бумаги, L(Q) - сумма длин
тех сторон клеток, которые лежат внутри его. Тогда L(Q) делится
на 4, так как все рассматриваемые стороны разбиваются на четверки
сторон, получающихся друг из друга поворотами на ±90°
и 180° относительно центра квадрата.
Если квадрат Q разделен на квадраты Q1, ј, Qn, то сумма длин
отрезков деления равна L(Q) – L(Q1) – ј – L(Qn). Ясно, что это число
делится на 4, так как числа L(Q), L(Q1), ј, L(Qn) делятся на 4.
-
23.11.
-
При перекрашивании горизонтали или вертикали, содержащей k черных
и 8 – k белых клеток, получится 8 – k черных и k белых клеток.
Поэтому число черных клеток изменится на (8 – k) – k = 8 – 2k, т. е. на
четное число. Так как четность числа черных клеток сохраняется, из
исходных 32 черных клеток мы не сможем получить одну черную клетку.
-
23.12.
-
При перекрашивании квадрата 2×2, содержащего k черных
и 4 – k белых клеток, получится 4 – k черных и k белых клеток.
Поэтому число черных клеток изменится на (4 – k) – k = 4 – 2k, т. е.
на четное число. Так как четность числа черных клеток сохраняется,
из исходных 32 черных клеток мы не сможем получить одну черную клетку.
-
23.13.
-
Диагонали разбивают многоугольник на несколько частей.
Будем называть соседними те из них, у которых есть общая сторона.
Ясно, что из любой внутренней точки многоугольника можно
попасть в любую другую, переходя каждый раз только из соседней
части в соседнюю. Часть плоскости, лежащую вне многоугольника,
также можно считать одной из этих частей. Число рассматриваемых
треугольников для точек этой части равно нулю, поэтому достаточно
доказать, что при переходе из соседней части в соседнюю четность
числа треугольников сохраняется.
Пусть общая сторона двух соседних частей лежит на диагонали (или
стороне) PQ. Тогда всем рассматриваемым треугольникам, кроме
треугольников со стороной PQ, обе эти части одновременно либо
принадлежат, либо не принадлежат. Поэтому при переходе из одной части
в другую число треугольников изменяется на k1 – k2, где k1 -
число вершин многоугольника, лежащих по одну сторону от PQ,
k2 - число вершин, лежащих по другую сторону от PQ. Так как
k1 + k2 = 2m – 2, то число k1 – k2 четно.
-
23.14.
-
Если хотя бы одно из расстояний между фишками
увеличилось бы, то увеличилась бы и сумма всех попарных расстояний
между фишками, но сумма всех попарных расстояний между фишками
не изменяется при любой перестановке.
-
23.15.
-
Пусть n - количество вершин исходного многоугольника,
n1, ј, np - количества вершин полученных многоугольников.
С одной стороны, сумма углов всех полученных многоугольников равна
|
p
е
i = 1
|
(ni – 2)p = |
p
е
i = 1
|
ni p – 2pp
|
. С другой стороны,
она равна 2(r – n) + (n – 2)p. Остается заметить, что
|
p
е
i = 1
|
ni = 2(q – n) + n
|
.
-
23.16.
-
Легко проверить, что длина границы всего заросшего
бурьяном участка (или нескольких участков) не возрастает. В начальный
момент она не превосходит 9 · 4 = 36, поэтому в конечный
момент она не может быть равной 40.
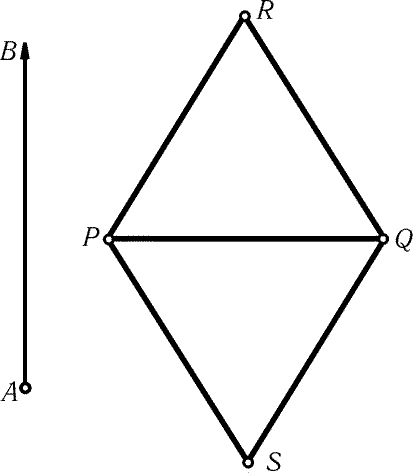
Рис. 23.9
23.17.
Фиксируем на плоскости некоторый луч AB. Любому
многоугольнику M поставим в соответствие число F(M) (зависящее
от AB) следующим образом. Рассмотрим все стороны M, перпендикулярные
AB, и каждой из них поставим в соответствие число ±l,
где l - длина этой стороны и знак «плюс» берется, если мы,
идя от этой стороны в направлении луча AB, попадаем внутрь M,
а знак «минус» - если наружу (рис. 23.8). Сумму всех полученных
чисел мы и обозначим F(M); если у M нет сторон, перпендикулярных
AB, то F(M) = 0.
Легко видеть, что если многоугольник M разрезан на многоугольники M1
и M2, то F(M) = F(M1) + F(M2), а если Mў получен из M
параллельным переносом, то F(Mў) = F(M). Поэтому, если M1
и M2 можно разрезать на части, переводящиеся друг в друга
параллельным переносом, то F(M1) = F(M2).
На рис. 23.9 изображены равные правильные треугольники PQR и PQS
и луч AB, перпендикулярный стороне PQ. Легко видеть,
что F(PQR) = a и F(PQS) = – a, где a - длина сторон этих правильных
треугольников. Поэтому равные треугольники PQR и PQS нельзя разрезать
на части, переводящиеся друг в друга параллельным переносом.
-
23.18.
-
Предположим, что выпуклый многоугольник M разрезан на невыпуклые
четырехугольники M1, ј, Mn. Каждому многоугольнику N
поставим в соответствие число f(N), равное разности между суммой его
внутренних углов, меньших 180°, и суммой углов, дополняющих
до 360° его углы, бóльшие 180°. Сравним числа
A = f(M) и B = f(M1) + ј + f(Mn). Рассмотрим для этого
все точки, являющиеся вершинами четырехугольников M1, ј, Mn.
Их можно разбить на четыре типа.
1. Вершины многоугольника M. Эти точки дают одинаковые
вклады в A и B.
2. Точки на сторонах многоугольника M или Mi. Вклад каждой
такой точки в B на 180° больше, чем в A.
3. Внутренние точки многоугольника, в которых сходятся углы
четырехугольника, меньшие 180°. Вклад каждой такой точки
в B на 360° больше, чем в A.
4. Внутренние точки многоугольника M, в которых сходятся
углы четырехугольников, причем один из них больше 180°. Такие
точки дают нулевые вклады в A и B.
В итоге получаем A Ј B. С другой стороны, A > 0, а B = 0.
Неравенство A > 0 очевидно, а для доказательства равенства B = 0
достаточно проверить, что если N - невыпуклый четырехугольник,
то f(N) = 0. Пусть углы N равны a і b і g і d.
У любого невыпуклого четырехугольника ровно один угол больше 180°,
поэтому f(N) = b + g + d – (360° – a) = a + b + g + d – 360° = 0°.
Получено противоречие, поэтому выпуклый многоугольник нельзя
разрезать на конечное число невыпуклых четырехугольников.
-
23.19.
-
Пусть Sn - окружность, построенная на n-м шаге, On -
ее центр. Рассмотрим величину
, где
суммирование ведется только по точкам, оказавшимся внутри окружности Sn.
Будем обозначать точки, лежащие внутри окружностей Sn и Sn + 1,
буквами B с индексом; точки, лежащие внутри окружности Sn, но вне
окружности Sn + 1, буквами C, а точки, лежащие внутри
окружности Sn + 1, но вне окружности Sn, буквами D. Тогда
| Fn = |
е
| (R2 – On Bi2) + |
е
| (R2 – On Ci2)
|
и
| Fn + 1 = |
е
| (R2 – On + 1Bi2) + |
е
| (R2 – On + 1 Di2). |
Так как
точка On + 1 является центром масс системы точек B и C, то
|
е
| On Bi2 + |
е
| On Ci2 = q OnOn + 12 + |
е
| On + 1Bi2 + |
е
| On + 1 Ci2,
|
где q - общее количество точек B и C.
Следовательно,
| Fn + 1 – Fn = q OnOn + 12 + |
е
| (R2 – On + 1Di2) – |
е
| (R2 – On + 1Ci2).
|
Все три слагаемых неотрицательны,
поэтому Fn + 1 і Fn.
В частности, Fn і F1 > 0, т. е. q > 0.
Центров масс различных наборов данных точек конечное число,
поэтому различных положений окружностей Si конечное число.
Следовательно, Fn + 1 = Fn для
некоторого n,
а значит, qOnOn + 12 = 0,
т. е. On = On + 1.
23.20.
Так как общее число клеток шахматной доски 5×5 клеток
нечетно, то черных и белых клеток не может быть поровну. Пусть
для определенности черных клеток больше. Тогда жуков, сидящих
на белых клетках, меньше, чем черных клеток. Поэтому хотя бы
одна из черных клеток останется пустой, так как на черные клетки
переползают только жуки. сидящие на белых клетках.
23.21.
Вырезаны поля одного цвета, пусть для определенности
черного. Поэтому остается 32 белых и 30 черных клеток. Так как
кость домино всегда накрывает одну белую и одну черную клетку,
то костями домино нельзя замостить шахматную доску 8×8 клеток,
из которой вырезаны два противоположных угловых поля.
23.22.
Предположим, что доска 10×10 клеток разбита на такие
фигурки. Каждая фигурка содержит либо 1, либо 3 черные клетки,
т. е. всегда нечетное число. Самих фигурок должно быть 100/4 = 25
штук. Поэтому они содержат нечетное число черных клеток, а всего
черных клеток 100/2 = 50 штук. Получено противоречие.
23.23.
Разрежем плоскость на одинаковые квадраты со стороной 2R
и раскрасим их в шахматном порядке. Впишем в каждый из
них окружность. Тогда детали полотна можно считать расположенными
на этих окружностях, причем движение поезда, идущего из
начала в конец, происходит в белых клетках по часовой стрелке,
а в черных - против (или наоборот; см. рис. 23.10). Поэтому тупик
образоваться не может, так как по обоим звеньям тупика движение
происходит в одну сторону.
-
23.24.
-
Рассмотрим решетку, изображенную на рис. 23.11, и раскрасим
ее в два цвета, как показано на этом рисунке (белые узлы на
этом рисунке не закрашены; исходный квадрат заштрихован, причем
кузнечики сидят в его белых вершинах). Докажем, что кузнечики
могут попасть только в бе-
лые узлы, т. е. при симметрии относительно
белого узла белый узел переходит в белый. Для этого достаточно
доказать, что при симметрии относительно
белого узла черный
узел переходит в черный. Пусть A - черный узел, B - белый,
а A1 - образ точки A при симметрии относительно B. Точка A1
является черным узлом тогда и только тогда, когда
, где m и n - целые числа. Ясно, что
|
®
AA1
|
= 2 |
®
AB
|
= 2(me1 + ne2)
|
, поэтому A1 - черный узел.
Таким образом, кузнечик не может попасть в четвертую вершину квадрата.
-
23.25.
-
Раскрасим узлы клетчатой бумаги в шахматном порядке (рис. 23.12). Так как
концы любого единичного отрезка разноцветны, то ломаная с
одноцветными концами содержит нечетное число узлов, а с разноцветными
- четное. Предположим, что из всех узлов границы (кроме вершин
квадрата) выходят ломаные. Докажем, что тогда все ломаные вместе
содержат четное число узлов. Для этого достаточно доказать, что число
ломаных с одноцветными концами четно. Пусть на границе квадрата
расположено 4m белых и 4n черных узлов (вершины квадрата не
учитываются). Обозначим число ломаных, у которых оба конца белые,
через k. Тогда имеется 4m – 2k ломаных с разноцветными концами
и [4n – (4m – 2k)]/2 = 2(n – m) + k ломаных с черными концами. Поэтому ломаных
с одноцветными концами будет k + 2(n – m) + k = 2(n – m + k) - четное
число. Остается заметить, что квадратный лист бумаги размером
100×100 клеток содержит нечетное число узлов. Поэтому ломаные,
содержащие четное число узлов, не могут проходить через все узлы.
-
23.26.
-
Раскрасим треугольники, как показано на рис. 23.13. Тогда черных
треугольников будет 1 + 2 + ј + n = n(n + 1)/2, а белых 1 + 2 + ј + (n – 1) = n(n – 1)/2. Ясно, что два треугольника с последовательными
номерами разноцветные. Поэтому среди занумерованных
треугольников черных может быть только на 1 больше, чем белых.
Следовательно, общее число занумерованных треугольников не
превосходит n(n – 1) + 1.
-
23.27.
-
Раскрасим дно коробки в два цвета, как показано на рис. 23.14.
Тогда каждая плитка 2×2 покрывает ровно одну черную клетку,
а плитка 1×4 покрывает 2 или 0. Поэтому четность числа черных
клеток дна коробки совпадает с четностью числа плиток 2×2.
Так как при замене плитки 2×2 на плитку 1×4 четность
числа плиток 2×2 изменится, выложить дно коробки плитками не
удастся.
-
23.28.
-
Заштрихуем на данном квадратном листе бумаги квадратики 2×2
так, как показано на рис. 23.15. При этом получится 100
заштрихованных квадратиков. Каждый вырезанный квадратик задевает
ровно один заштрихованный квадратик, поэтому хотя бы один
заштрихованный квадратик остается целым, и его можно вырезать.

Рис. 23.16
23.29.
Если многоугольник разбит на части несколькими диагоналями, то эти
части можно окрасить в два цвета так, чтобы части, имеющие общую
сторону, были разного цвета. Это можно сделать следующим образом. Будем
последовательно проводить диагонали. Каждая диагональ разбивает
многоугольник на две части. В одной из них сохраняем раскраску, а
другую перекрашиваем, заменяя везде белый цвет на черный, а черный -
на белый. Проделав эту операцию для всех нужных диагоналей, получим
требуемую раскраску. Так как в нашем случае в каждой вершине сходится
нечетное число треугольников, то при такой раскраске все стороны
многоугольника будут принадлежать треугольникам одного цвета,
например черного (рис. 23.16). Обозначим число сторон белых треугольников
через m. Ясно, что m делится на 3. Так как каждая сторона белого
треугольника является также и стороной черного треугольника, а все стороны
многоугольника являются сторонами черных треугольников, то число
сторон черных треугольников равно n + m. Поэтому n + m делится
на 3, а поскольку m делится на 3, то и n делится на 3.

Рис. 23.18
23.30.
Раскрасим доску в четыре цвета, как показано на рис. 23.17.
Легко сосчитать, что клеток второго цвета 26, а четвертого 24.
Каждая плитка 1×4 накрывает по одной клетке каждого цвета.
Поэтому плитками 1×4 нельзя замостить доску 10×10,
так как иначе клеток каждого цвета было бы поровну.
23.31.
Раскрасим клетчатую бумагу в четыре цвета, как показано
на рис. 23.18. Среди данных n клеток найдется не менее n/4 одноцветных
клеток, а одноцветные клетки не имеют общих точек.
23.32.
Раскрасим узлы клетчатой бумаги в четыре цвета в том
же порядке, в каком раскрашены клетки на рис. 23.18. Если n і 5,
то найдутся две одноцветные вершины n-угольника. Середина отрезка
с концами в одноцветных узлах является узлом. Так как n-угольник
выпуклый, то середина отрезка с концами в его вершинах лежит либо
внутри его, либо на стороне.
-
23.33.
-
Разобьем полученный квадрат на клетки размером 1×1 и раскрасим
их в три цвета, как показано на рис. 23.19. Легко проверить, что плитки
1×3 можно разбить на два типа: плитка 1-го типа накрывает одну
клетку 1-го цвета и две клетки 2-го цвета, а плитка 2-го типа
накрывает одну клетку 2-го цвета и две клетки 3-го цвета.
Предположим, что все клетки 1-го цвета накрыты плитками 1×3.
Тогда плиток 1-го типа 9, а плиток 2-го типа 7. Следовательно,
они накрывают 9 · 2 + 7 = 25 клеток 2-го цвета и 7 · 2 = 14
клеток 3-го цвета. Получено противоречие, поэтому одна из клеток 1-го
цвета накрыта плиткой 1×1.
-
23.34.
-
Разрежем данный n-угольник непересекающимися диагоналями на треугольники
(см. задачу 22.23). Вершины n-угольника можно раскрасить в три цвета
так, что все вершины каждого из полученных треугольников будут разного
цвета (см. задачу 23.40). Вершин какого¯нибудь цвета будет не более
[n/3]; сторожей достаточно поставить в этих вершинах.
-
23.35.
-
Рассмотрим правильный треугольник со стороной 1. Все
три его вершины не могут быть разного цвета, поэтому две
вершины имеют один цвет; расстояние между ними равно 1.
-
23.36.
-
Предположим, что любые две точки, лежащие на расстоянии 1, окрашены
в разные цвета. Рассмотрим правильный треугольник ABC со стороной 1;
все его вершины разного цвета. Пусть точка A1 симметрична A
относительно прямой BC. Так как A1B = A1C = 1, то цвет точки A1
отличен от цветов точек B и C, т. е. она окрашена в тот же цвет,
что и точка A. Эти рассуждения показывают, что если AA1 = Ц3,
то точки A и A1 одного цвета. Поэтому все точки окружности
радиуса Ц3 с центром A одного цвета. Ясно, что на этой
окружности найдутся две точки, расстояние между которыми равно 1.
Получено противоречие.
-
23.37.
-
Приведем пример раскраски плоскости в семь цветов, для
которой расстояние между любыми двумя одноцветными точками
не равно 1. Разобьем плоскость на равные шестиугольники со
стороной a и окрасим их, как показано на рис. 23.20 (точки, принадлежащие
двум или трем шестиугольникам, можно красить в любой
из цветов этих шестиугольников). Наибольшее расстояние между
точками одного цвета, лежащими в одном шестиугольнике, не
превосходит 2a, а наименьшее расстояние между точками одного
цвета, лежащими в разных шестиугольниках, не меньше длины
отрезка AB (см. рис. 23.20). Ясно, что AB2 = AC2 + BC2 = 4a2 + 3a2 = 7a2 > (2a)2.
Поэтому, если 2a < 1 < Ц7 a, т. е. 1/Ц7 < a < 1/2, то
расстояние между точками одного цвета не может быть равно 1.
-
23.38.
-
Предположим, что нет прямоугольного треугольника с вершинами одного
цвета. Разделим каждую сторону правильного
треугольника двумя точками на три равные части. Эти точки
образуют правильный шестиугольник. Если две его
противоположные
вершины одного цвета, то все остальные вершины будут второго
цвета, а значит, есть прямоугольный треугольник с вершинами
второго цвета. Следовательно, противоположные вершины шестиугольника
разноцветные. Поэтому найдутся две соседние разноцветные вершины;
противоположные им вершины тоже разноцветные.
Одна из этих пар разноцветных вершин лежит на стороне треугольника.
Точки этой стороны, отличные от вершин шестиугольника,
не могут быть ни первого, ни второго цвета. Получено противоречие.
-
23.39.
-
Докажем это утверждение индукцией по числу треугольников триангуляции.
Для одного треугольника требуемая раскраска существует. Предположим
теперь, что можно раскрасить требуемым образом любую триангуляцию,
состоящую менее чем из n треугольников, и докажем, что тогда можно
раскрасить любую триангуляцию, состоящую из n треугольников. Выбросим
треугольник, одна из сторон которого лежит на стороне триангулированной
фигуры. Оставшуюся часть можно раскрасить по предположению индукции
(она, конечно, может состоять из нескольких кусков, но это не мешает).
У выброшенного треугольника только две стороны могут граничить с остальными
треугольниками. Поэтому его можно окрасить в цвет, отличный от
цветов двух соседних с ним треугольников.
-
23.40.
-
Доказательство аналогично решению задачи 23.39. Главное
отличие заключается в том, что выбрасывать нужно треугольник,
выходящий двумя сторонами на границу многоугольника (см. задачу 22.26).
-
23.41.
-
Доказательство проведем индукцией по числу кругов n. При
n = 1 утверждение очевидно. Пусть M - любая точка, O -
наиболее удаленный от нее центр круга. Тогда круг с центром O
касается не более трех других данных кругов. Выбросим его и раскрасим
остальные круги согласно предположению индукции. Этот круг можно
окрасить цветом, отличным от цветов касающихся его кругов.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:47.

 Глава 23. § -1 |
Глава 23. § -1 | 

 Глава 23. § -1 |
Глава 23. § -1 | 

