Глава 24. § -1  |	Оглавление |	Глава 25.

24.1.

Предположим, что вершины правильного треугольника ABC расположены в узлах целочисленной решетки. Тогда тангенсы всех углов, образованных сторонами AB и AC с линиями решетки, рациональны. При любом положении треугольника ABC сумма или разность некоторых двух таких углов a и b равна 60°. Следовательно, Ц3 = tg 60° = tg (a±b) = (tg a±tg b)/(1-±tg atg b) - рациональное число. Получено противоречие.

24.2.

Для n = 3 и n = 6 утверждение вытекает из предыдущей задачи, поэтому будем в дальнейшем считать, что n № 3, 4, 6. Предположим, что существуют правильные n-угольники с вершинами в узлах целочисленной решетки (n № 3, 4, 6). Среди всех таких n-угольников можно выбрать тот, у которого длина стороны наименьшая. (Для доказательства достаточно заметить, что если a - длина отрезка с концами в узлах решетки, то

a =

Ц

n2 + m2

, где n и m - целые числа, т. е. имеется лишь конечное число различных длин отрезков с концами в узлах решетки, меньших данной длины.). Пусть

® AiBi

=

® Ai + 1Ai + 2

. Тогда B₁јB_n - правильный n-угольник, вершины которого лежат в узлах целочисленной решетки, а его сторона меньше стороны n-угольника A₁јA_n. Для n = 5 это видно из рис. 24.1, а для n і 7 - из рис. 24.2. Получено противоречие с выбором n-угольника A₁јA_n.

Рис. 24.1 Рис. 24.2

24.3.

Легко проверить, что треугольник с вершинами в точках с координатами (0, 0), (12, 16) и ( – 12, 9) обладает требуемыми свойствами.

24.4.

Предположим, что существует замкнутая ломаная A₁јA_n с  нечетным числом звеньев равной длины, все вершины которой лежат в узлах целочисленной решетки. Пусть a_i и b_i - координаты проекций вектора

® AiAi + 1

на горизонтальную и  вертикальную оси. Обозначим длину звена ломаной через c. Тогда c² = a_i² + b_i², поэтому c² при делении на 4 дает остаток 0, 1 или 2. Если c² делится на 4, то a_i и b_i делятся на 4 (это доказывается простым перебором всех возможных остатков, которые a_i и b_i дают при делении на 4). Поэтому при гомотетии с центром A₁ и коэффициентом 0,5 наша ломаная перейдет в ломаную с меньшей длиной звена, вершины которой по-прежнему лежат в узлах решетки. После нескольких таких операций придем к ломаной, у которой c² не делится на 4, т. е. дает остаток 1 или 2. Разберем эти варианты, предварительно заметив, что a₁ + ј + a_m = b₁ + ј + b_m = 0.

2. c² при делении на 4 дает остаток 1. Тогда одно из чисел a_i и b_i нечетно, а другое четно, поэтому число a₁ + ј + a_m + b₁ + ј + b_m нечетно и не может равняться нулю.

24.5.

Каждому многоугольнику N с вершинами в узлах целочисленной решетки поставим в соответствие число f(N) = n + m/2 – 1. Пусть многоугольник M разрезан на многоугольники M₁ и M₂ с вершинами в узлах решетки. Докажем, что если формула Пика верна для двух из многоугольников M, M₁ и M₂, то она верна и  для третьего. Для этого достаточно доказать, что f(M) = f(M₁) + f(M₂). Узлы, по которым разрез не проходит, дают одинаковые вклады в f(M) и в f(M₁) + f(M₂). «Неконцевые» узлы разреза дают в f(M) вклад 1, а в f(M₁) и в  f(M₂) - по 0,5. Каждый же из двух концевых узлов разреза дает в f(M), f(M₁) и f(M₂) вклады по 0,5, поэтому вклад концевых узлов в f(M) на 1 меньше, чем в f(M₁) + f(M₂). Так как в f(M) из всех вкладов вычитается 1, а в f(M₁) + f(M₂) вычитается 2, то f(M) = f(M₁) + f(M₂).

Для завершения доказательства формулы Пика остается заметить, что любой многоугольник можно разрезать диагоналями на треугольники.

Рис. 24.3

24.6.

Согласно формуле Пика S_AOB = S_BOC = S_COA = 1/2, а значит, O - точка пересечения медиан треугольника ABC (см. задачу 4.2).

24.7.

Возьмем какой¯нибудь достаточно большой квадрат со стороной 2ⁿ так, чтобы все черные клетки лежали внутри его и составляли менее 0,2 его площади. Разрежем этот квадрат на четыре одинаковых квадрата. Каждый из них окрашен менее чем на 0,8. Те из них, которые окрашены более чем на 0,2, оставляем, а остальные режем дальше таким же образом. Полученные квадраты 2×2 будут окрашены на 1/4, 1/2, 3/4 или не будут окрашены вовсе. Из листа бумаги нужно вырезать те полученные квадраты, в которых есть окрашенные клетки.

24.8.

Рассмотрим все выпуклые фигуры, получающиеся из данной переносами на векторы, обе координаты которых четны. Докажем, что хотя бы две из этих фигур пересекаются. Исходную фигуру можно заключить в круг радиуса R с центром в начале координат, причем R можно выбрать целым числом. Возьмем те из рассматриваемых фигур, координаты центров которых являются неотрицательными числами, не превосходящими 2n. Этих фигур ровно (n + 1)² штук и все они лежат внутри квадрата со стороной 2(n + R). Если бы они не пересекались, то при любом n выполнялось бы неравенство (n + 1)² S < 4(n + R)², где S - площадь данной фигуры. Но так как S > 4, то n можно выбрать так, чтобы выполнялось неравенство

(n + R)/(n + 1) <

Ц

S/4

.

Рис. 24.4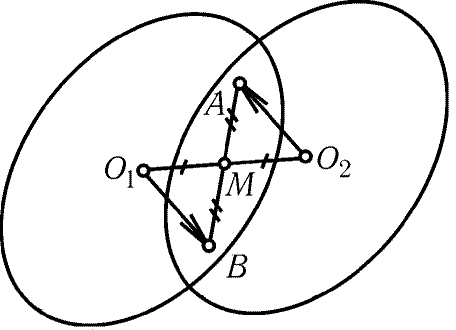

Рис. 24.5

Пусть

® O1B

=  –

® O2A

. Так как данная фигура центрально симметрична, точка B принадлежит фигуре с центром O₁. Эта фигура выпукла, и точки A и B принадлежат ей, поэтому ей принадлежит также середина отрезка AB. Ясно, что середина отрезка AB совпадает с серединой отрезка O₁O₂.

24.9. Пусть охотник находится в точке O, а заяц - в точке A; A₁ - точка, симметричная A относительно O. Рассмотрим фигуру F, содержащую все точки, расстояние от которых до отрезка AA₁ не превосходит r (рис. 24.5). Достаточно доказать, что F содержит хотя бы один узел решетки (если узел попадает в заштрихованную часть, то точка A принадлежит стволу дерева).

Площадь F равна 4rh + pr², где h - расстояние от охотника до зайца. Если h > 1/r, то 4rh + pr² > 4. По теореме Минковского F содержит целочисленную точку.

24.10.

Рассмотрим целочисленную решетку, заданную уравнениями x = k + 1/2 и y = l + 1/2, где k и l - целые числа. Докажем, что каждый квадрат этой решетки дает неотрицательный вклад в величину n – S + p. Рассмотрим два случая.

2. Фигура пересекает квадрат, но не содержит его центр. Докажем, что в этом случае Sў Ј pў; при этом можно ограничиться рассмотрением случаев, изображенных на рис. 24.6 (т. е. можно считать, что центр O квадрата лежит на границе фигуры). Так как расстояния от центра квадрата до его сторон равны 1/2, то pў і 1/2. Проведя через точку O опорную прямую к данной фигуре, получим, что Sў Ј 1/2.

Ясно также, что все вклады квадратов не могут быть одновременно нулевыми.

Рис. 24.6

24.11.

Докажем сначала, что на окружности с центром A = (Ц2, 1/3) не может лежать более одной целочисленной точки. Если m и n - целые числа, то (m – Ц2)² + (n – (1/3))² = q – 2mЦ2, где q - рациональное число. Поэтому из равенства

(m1 – Ц2)2 + (n1 – 1/3)2 = (m2 – Ц2)2 + (n2 – (1/3))2

следует, что m₁ = m₂. По теореме Виета сумма корней уравнения (n – (1/3))² = d равна 2/3, поэтому лишь один корень может быть целочисленным.

24.12.

Докажем сначала, что уравнение x² + y² = 5^k имеет ровно 4(k + 1) целочисленных решений. При k = 0 и k = 1 это утверждение очевидно. Докажем, что уравнение x² + y² = 5^k имеет ровно восемь таких решений (x, y), что x и y не делятся на 5; вместе с  4(k – 1) решениями вида (5a, 5b), где a и b - решение уравнения a² + b² = 5^k – 2, они дают нужное количество решений. Эти решения получаются друг из друга перестановками x и y и  изменениями знаков; мы будем называть их нетривиальными решениями.

Если (x, y) - нетривиальное решение уравнения x² + y² = 5^k, то (x + 2y, 2x – y) и (x – 2y, 2x + y) - решения уравнения x² + h² = 5^k + 1, причем ровно одно из них нетривиально. Остается доказать, что нетривиальное решение единственно с точностью до перестановки x и y и изменения знаков. Пусть (x, y) - нетривиальное решение уравнения x² + y² = 5^k. Тогда как пары

ж и

±

2x – y 5

, ±

x + 2y 5

ц ш

и 

ж и

±

x + 2y 5

,

±

2x – y 5

ц ш

, так и пары

ж и

±

2x + y 5

, ±

x – 2y 5

ц ш

и 

ж и

±

x – 2y 5

, ±

2x + y 5

ц ш

являются решениями уравнения x² + h² = 5^k – 1, но целочисленными будут пары ровно одного из этих видов, так как ровно одно из чисел x + 2y и x – 2y делится на 5. При этом мы получим нетривиальное решение, потому что (x + 2y)(x – 2y) = (x² + y²) – 5y² при k і 2 делится на 5, но не делится на 25. Таким образом, каждое из восьми нетривиальных решений уравнения x² + y² = 5^k дает восемь нетривиальных решений уравнения x² + h² = 5^k – 1, причем для одной половины решений нужно воспользоваться формулами первого вида, а для другой половины решений - формулами второго вида.

Перейдем теперь непосредственно к решению задачи. Пусть n = 2k + 1. Докажем, что на окружности радиуса 5^k/3 с центром (1/3, 0) лежит ровно n целочисленных точек. Уравнение x² + y² = 5^2k имеет 4(2k + 1) целочисленных решений. Кроме того, 5^2k при делении на 3 дает остаток 1, поэтому одно из чисел x и y делится на 3, а другое при делении на 3 дает остаток ±1. Следовательно, ровно в одной из пар (x, y), (x,  – y), (y, x) и ( – y, x) первое и второе числа дают при делении на 3 остатки  – 1 и 0 соответственно. Поэтому уравнение (3z – 1)² + (3t)² = 5^2k имеет ровно 2k + 1 целочисленных решений.

Пусть n = 2k. Докажем, что на окружности радиуса 5^{(k – 1)/2}/2 с центром (1/2, 0) лежит ровно n целочисленных точек. Уравнение x² + y² = 5^k – 1 имеет ровно 4k целочисленных решений, причем одно из чисел x и y четно, а другое нечетно. Поэтому уравнение (2z – 1)² + (2t)² = 5^k – 1 имеет ровно 2k целочисленных решений.

Глава 24. § -1  |	Оглавление |	Глава 25.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.