Глава 26. § -1  |	Оглавление |	Глава 27.

26.1.

а) Легко проверить, что, построив четвертое здание внутри треугольника, образованного тремя другими зданиями, получим требуемое расположение.

26.2.

Можно считать, что n і 4 и не все точки лежат на одной прямой. Тогда можно выбрать четыре точки A, B, C и D, не лежащие на одной прямой. По условию три из них лежат на одной прямой. Пусть для определенности точки A, B и C лежат на прямой l, а D не лежит на l. Нужно доказать, что все точки, кроме D, лежат на прямой l. Предположим, что точка E не принадлежит l. Рассмотрим четверку точек A, B, D, E. Тройки точек A, B, D и A, B, E не лежат на одной прямой. Поэтому на одной прямой лежит либо тройка точек A, D, E, либо тройка точек B, D, E. Пусть для определенности на одной прямой лежат точки A, D и E. Тогда никакие три из точек B, C, D, E не лежат на одной прямой. Получено противоречие.

26.3.

Пусть количество различных расстояний между точками равно k. Фиксируем две точки. Тогда все остальные точки являются точками пересечения двух семейств концентрических окружностей, содержащих по k окружностей. Следовательно, общее количество точек не превосходит 2k² + 2. Остается заметить, что 2 · 14² + 2 = 394 < 400.

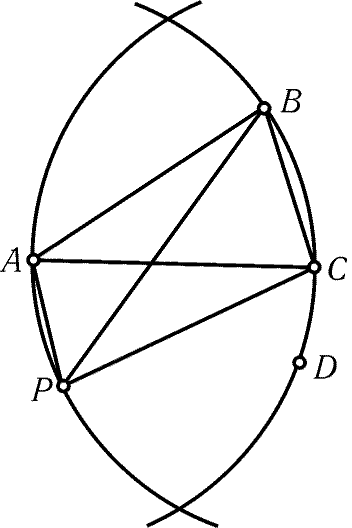
Рис. 26.1

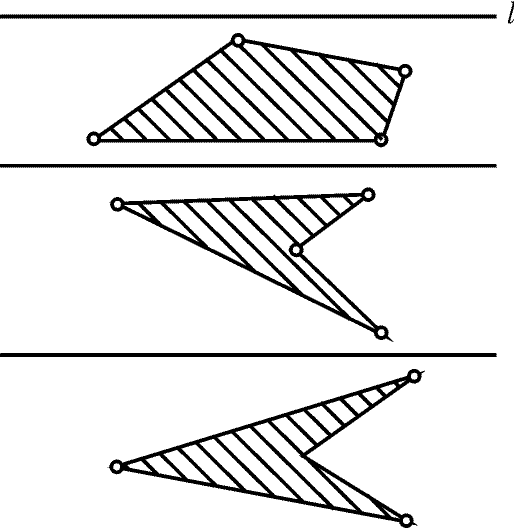
Рис. 26.2

26.4. Назовем диаметром отрезок длиной d, соединяющий пару данных точек. Концы всех диаметров, выходящих из точки A, лежат на окружности с центром A и радиусом d. Так как расстояние между любыми двумя точками не превосходит d, концы всех диаметров, выходящих из A, лежат на дуге, угловая величина которой не превосходит 60°. Следовательно, если из точки A выходят три диаметра AB, AC и AD, то один из концов этих диаметров лежит внутри угла, образованного двумя другими. Пусть для определенности точка C лежит внутри угла BAD. Докажем, что тогда из точки C выходит не более одного диаметра. Предположим, что есть еще диаметр CP и точки B и P лежат по разные стороны от прямой AC (рис. 26.1). Тогда ABCP - выпуклый четырехугольник, поэтому AB + CP < AC + BP (см. задачу 9.14), т. е. d + d < d + BP, а значит, BP > d, чего не может быть.

В итоге получаем, что либо из каждой точки выходит не более двух диаметров, либо существует точка, из которой выходит не более одного диаметра. Теперь требуемое утверждение можно доказать индукцией по числу точек. Для n = 3 оно очевидно. Предположим, что утверждение доказано для любой системы из n точек, и докажем его для системы из n + 1 точки. В этой системе либо есть точка, из которой выходит не более одного диаметра, либо из каждой точки выходит не более двух диаметров. В первом случае отбрасываем эту точку и, воспользовавшись тем, что в оставшейся системе не более n диаметров, получаем требуемое. Второй случай очевиден.

26.5. Проведем все прямые, соединяющие пары данных точек, и выберем прямую l, не параллельную ни одной из них. Прямыми, параллельными l, можно разбить данные точки на четверки. Четырехугольники с вершинами в этих четверках точек искомые (рис. 26.2).

26.6. Разобьем данные точки произвольным образом на шесть групп: четыре группы по четыре точки, группа из пяти точек и группа из одной точки. Рассмотрим группу из пяти точек. Из них можно выбрать четыре точки, являющиеся вершинами некоторого выпуклого четырехугольника ABCD (см. задачу 22.2). Объединим в пары точки A, C и B, D. Тогда отрезки AC и BD, заданные парами, пересекаются. Одна из пяти точек осталась свободной. Присоединим ее к четверке точек и с полученной пятеркой точек проделаем то же самое и т. д. После пяти таких операций останутся две точки, и мы объединим их в пару.

26.7.

Так как

ж и

2n n2 + 1

ц ш

2

+

ж и

n2 – 1 n2 + 1

ц ш

2

= 1

, то существует угол j, обладающий тем свойством, что sin j  = 2n/(n² + 1) и cos j  = (n² – 1)/(n² + 1), причем 0 < 2Nj < p/2 при достаточно большом n. Рассмотрим окружность радиуса R с центром O и возьмем на ней точки A₀, A₁, ј, A_N – 1 так, что РA₀OA_k = 2kj. Тогда A_iA_j = 2Rsin (|i – j|j). Воспользовавшись формулами sin (m + 1)j  =  sin mjcos j + sin jcos mj и cos (m + 1)j  =  cos mjcos j – sin mjsin j, легко доказать, что числа sin mj и cos mj рациональны для всех натуральных m. Возьмем в качестве R наибольший общий делитель всех знаменателей рациональных чисел sin j, ј, sin (N – 1)j. Тогда A₀, ј, A_N – 1 - требуемая система точек.

26.8.

Требуемый пример изображен на рис. 26.3.

26.9.

Можно. Пример изображен на рис. 26.4.

Рис. 26.3 Рис. 26.4

26.10.

Из условия следует, что все вершины многоугольника разбиваются на пары, задающие диагонали A_iA_j, которые проходят через точку O. Поэтому число вершин четно и по обе стороны от каждой такой диагонали A_iA_j лежит равное число вершин. Следовательно, j = i + m, где m - половина числа вершин. Таким образом, точка O является точкой пересечения диагоналей, соединяющих противоположные вершины. Ясно, что точка пересечения этих диагоналей единственна.

26.11.

Если AC и BD - пересекающиеся красные отрезки, то число точек пересечения любой прямой с отрезками AB и CD не превосходит числа точек пересечения этой прямой с отрезками AC и BD. Поэтому, заменив красные отрезки AC и BD на отрезки AB и CD, мы не увеличим число точек пересечения красных отрезков с синими, а число точек пересечения красных отрезков с красными уменьшим, так как исчезнет точка пересечения AC и BD. После нескольких таких операций все красные отрезки станут непересекающимися, и нам остается доказать, что в этом случае число точек пересечения красных отрезков с синими не меньше n. Рассмотрим произвольный красный отрезок. Так как другие красные отрезки его не пересекают, то по обе стороны от него лежит четное число красных точек, т. е. нечетное число синих точек. Следовательно, найдется синий отрезок, пересекающий данный красный отрезок. Поэтому числе точек пересечения красных отрезков с синими не меньше числа красных отрезков, т. е. не меньше n.

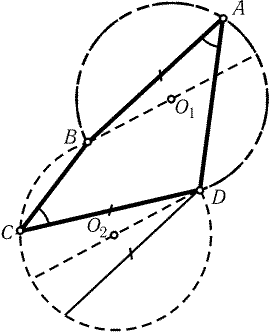
Рис. 26.5

26.12. Пусть A - общая точка первых трех окружностей S₁, S₂ и S₃. Обозначим точки пересечения окружностей S₁ и S₂, S₂ и S₃, S₃ и S₁ через B, C, D соответственно. Предположим, что существует окружность S, не проходящая через точку A. Тогда окружность S проходит через точки B, C и D. Пусть Sў - пятая окружность. Каждая пара точек из набора A, B, C, D является парой точек пересечения двух из окружностей S₁, S₂, S₃, S. Поэтому окружность Sў проходит через одну точку из каждой пары точек A, B, C, D. С другой стороны, окружность Sў не может проходить через три точки из A, B, C, D, поскольку каждая тройка этих точек задает одну из окружностей S₁, S₂, S₃, S. Поэтому окружность Sў не проходит через какие-то две из этих точек. Получено противоречие.

26.13. Рассмотрим прямоугольник ABCD со сторонами AB = 1 см и BC = 500 м. Пусть O - точка пересечения его диагоналей. Легко проверить, что площадь треугольника AOD больше 1 м², а все его высоты меньше 1 см.

26.14. Нет, не обязательно. На рис. 26.5 показано, как получить нужный четырехугольник ABCD.

26.15.

Не обязательно. Легко проверить, что список длин сторон и диагоналей для равнобедренной трапеции с высотой 1 и основаниями 2 и 4 совпадает с таким же списком для четырехугольника с перпендикулярными диагоналями длиной 2 и 4, делящимися точкой пересечения на отрезки длиной 1 и 1, 1 и 3 (рис. 26.6).

Рис. 26.6

26.16.

Да, существуют. Рассмотрим точки P_i = (i, i²), где i = 1, ј, n. Площади всех треугольников с вершинами в узлах целочисленной решетки рациональны (см. задачу 24.5), а числа

PiPj = |i – j|

Ц

1 + (i + j)2

иррациональны.

26.17.

Да, существуют. Пусть C - середина отрезка AB. Тогда XC² = (2XA² + 2XB² – AB²)/2. Если число AB² иррационально, то числа XA, XB и XC не могут одновременно быть рациональными.

26.18.

Может. Рассмотрим прямоугольный треугольник ABC₁ с катетами AB = 1 и BC₁ = 2n. Проведем в нем медиану AM₁, биссектрису BK₁ и высоту C₁H₁. Площадь треугольника, образованного этими отрезками, больше S_ABM1 – S_ABK1. Ясно, что S_ABK1 < 1/2 и S_ABM1 = n/2, т. е. S_ABM1 – S_ABK1 > (S/2) – (S/2n), где S = S_ABC1. Поэтому при достаточно большом n площадь треугольника, образованного отрезками AM₁, BK₁ и C₁H₁, будет больше 0,499 S.

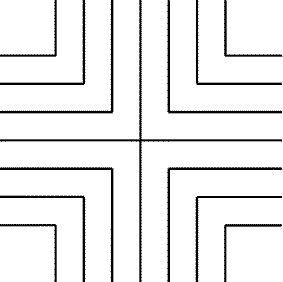
Рис. 26.7

Точку C₁ можно слегка сдвинуть так, чтобы прямоугольный треугольник ABC₁ превратился в остроугольный треугольник ABC, а площадь треугольника, образованного точками пересечения отрезков, осталась больше 0,499 площади треугольника ABC.

26.19. Можно. Замостим, например, бесконечные уголки, изображенные на рис. 26.7.

26.20. Да, может. Докажем это утверждение индукцией, заменив 100 на n. При n = 1 можно взять концы отрезка длиной 1. Предположим, что утверждение доказано для n и A₁, ј, A_k - нужный набор точек. Пусть A₁ў, ј, A_kў - образы точек A₁, ј, A_k при параллельном переносе на единичный вектор a. Для доказательства шага индукции единичный вектор a достаточно выбрать так, что

a №

® AiAj

и A_jA_iў № 1 при i № j, т. е.

|

® AjAi

+ a| № 1

при i № j. Каждое из этих ограничений исключает из единичной окружности не более одной точки.

26.21.

Не всегда. Рассмотрим отрезки, изображенные на рис. 26.8. Концы каждого короткого отрезка можно соединить только с концами ближайшего к нему длинного отрезка. Ясно, что при этом не может получиться замкнутая несамопересекающаяся ломаная.

Рис. 26.8 Рис. 26.9

26.22.

Не обязательно. Докажем, что центр O вписанной окружности треугольника ABC со сторонами AB = 6, BC = 4 и CA = 8 одинаково удален от середин сторон AC и BC. Обозначим середины сторон AC и BC через B₁ и A₁, а основания перпендикуляров, опущенных из точки O на AC и BC, - через B₂ и A₂ (рис. 26.9). Так как A₁A₂ = 1 = B₁B₂ (см. задачу 3.2) и OA₂ = OB₂, то DOA₁A₂ = DOB₁B₂ т. е. OA₁ = OB₁.

26.23.

Это возможно при любом n і 2. Впишем в арену правильный k-угольник, где k - число различных пар, которые можно составить из n прожекторов, т. е. k = n(n – 1)/2. Тогда можно установить взаимно однозначное соответствие между сегментами, отсекаемыми сторонами k-угольника, и парами прожекторов. Пусть каждый прожектор освещает весь k-угольник и сегменты, соответствующие парам прожекторов, в которые он входит. Легко проверить, что это освещение обладает требуемыми свойствами.

Глава 26. § -1  |	Оглавление |	Глава 27.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.