Глава 28. § 4  |	Оглавление |	Глава 28. § 6

§ 5.  Точки, лежащие на одной окружности, и окружности, проходящие через одну точку

Рис. 28.2

28.31. Даны четыре окружности, причем окружности S₁ и S₃ пересекаются с обеими окружностями S₂ и S₄. Докажите, что если точки пересечения S₁ с S₂ и S₃ с S₄ лежат на одной окружности или прямой, то и точки пересечения S₁ с S₄ и S₂ с S₃ лежат на одной окружности или прямой (рис. 28.2).

                       28.32^*. Даны четыре окружности S₁, S₂, S₃, S₄. Пусть S₁ и S₂ пересекаются в точках A₁ и A₂, S₂ и S₃ - в точках B₁ и B₂, S₃ и S₄ - в точках C₁ и C₂, S₄ и S₁ - в точках D₁ и D₂ (рис. 28.3). Докажите, что если точки A₁, B₁, C₁, D₁ лежат на одной окружности S (или прямой), то и точки A₂, B₂, C₂, D₂ лежат на одной окружности (или прямой).

28.33^*.

Стороны выпуклого пятиугольника ABCDE продолжили так, что образовалась пятиконечная звезда AHBKCLDMEN (рис. 28.4). Около треугольников - лучей звезды описали окружности. Докажите, что пять точек пересечения этих окружностей, отличных от A, B, C, D, E, лежат на одной окружности.

28.34^*.

На плоскости взяты шесть точек A₁, A₂, A₃, B₁, B₂, B₃. Докажите, что если описанные окружности треугольников

Рис. 28.3 A₁A₂B₃, A₁B₂A₃ и B₁A₂A₃ проходят через одну точку, то и описанные окружности треугольников B₁B₂A₃, B₁A₂B₃ и A₁B₂B₃ пересекаются в одной точке.

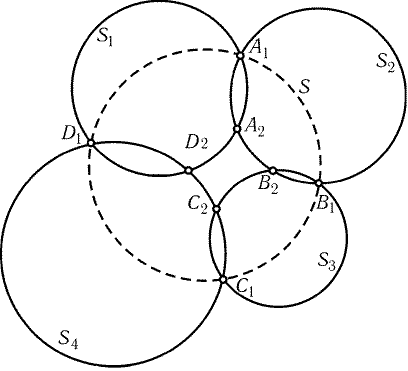
28.35^*. На плоскости взя-
ты шесть точек A₁, A₂, B₁, B₂, C₁, C₂. Докажите, что если окружности, описанные около треугольников A₁B₁C₁, A₁B₂C₂, A₂B₁C₂, A₂B₂C₁, проходят через одну точку, то и окружности, описанные около треугольников A₂B₂C₂, A₂B₁C₁, A₁B₂C₁, A₁B₁C₂, проходят через одну точку.

Рис. 28.4

28.36^*. В этой задаче мы будем рассматривать наборы из n прямых общего положения, т. е. наборы, в которых никакие две прямые не параллельны и никакие три не проходят через одну точку.

                      Набору из двух прямых общего положения поставим в соответствие точку - их точку пересечения, а набору из трех прямых общего положения - окружность, проходящую через три точки пересечения. Если l₁, l₂, l₃, l₄ - четыре прямые общего положения, то четыре окружности S_i, соответствующие четырем тройкам прямых, получаемых отбрасыванием прямой l_i, проходят через одну точку (см. задачу 2.85, а)), которую мы и поставим в соответствие четверке прямых. Эту конструкцию можно продолжить.

а) Пусть l_i, i = 1, ј, 5 - пять прямых общего положения. Докажите, что пять точек A_i, соответствующих четверкам прямых, получаемых отбрасыванием прямой l_i, лежат на одной окружности.

б) Докажите, что эту цепочку можно продолжить, поставив в  соответствие каждому набору из n прямых общего положения точку при четном n и окружность при нечетном n, так, что n окружностей (точек), соответствующих наборам из n – 1 прямых, проходят через эту точку (лежат на этой окружности).

28.37^*.

Пусть на двух пересекающихся прямых l₁ и l₂ выбраны точки M₁ и M₂, не совпадающие с точкой пересечения M этих прямых. Поставим в соответствие им окружность, проходящую через M₁, M₂ и M.

а) Пусть l₁, l₂, l₃, l₄ - четыре прямые общего положения, на каждой из которых задано по точке, причем эти точки лежат на одной окружности. Докажите, что четыре точки, соответствующие тройкам, получаемым отбрасыванием одной из прямых, лежат на одной окружности.

б) Докажите, что каждому набору из n прямых общего положения с заданными на них точками, лежащими на одной окружности, можно поставить в соответствие точку (при нечетном n) или окружность (при четном n) так, что n окружностей (точек при четном n), соответствующих наборам из n – 1 прямых, проходят через эту точку (лежат на этой окружности при четном n).

Глава 28. § 4  |	Оглавление |	Глава 28. § 6

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.