Глава 28. § -1  |	Оглавление |	Глава 29.

28.1.

Пусть R² - степень инверсии. Тогда OA · OA^* = OB · OB^*  =  R², откуда OA : OB = OB^* : OA^* и DOAB ~ DOB^*A^*, поскольку РAOB = РB^*OA^*.

28.2.

Опустим из точки O перпендикуляр OC на прямую l и возьмем произвольную точку M на l. Из подобия треугольников OCM и OM^*C^* (задача 28.1) следует, что РOM^*C^* = РOCM  =  90°, т. е. точка M^* лежит на окружности S с диаметром OC^*. Если X - какая-то точка S, отличная от O, то она является образом при инверсии точки Y пересечения прямых l и OX (так как образ точки Y лежит, с одной стороны, на луче OX, а с другой стороны, как уже доказано, на окружности S). Итак, инверсия переводит прямую l в окружность S (без точки O).

28.3.

Случай, когда окружность S проходит через O, фактически был разобран в предыдущей задаче (и формально следует из нее, так как (M^*)^* = M). Предположим теперь, что точка O не принадлежит S. Пусть A и B - точки пересечения окружности S с прямой, проходящей через O и центр S, а M - произвольная точка S. Докажем, что образом S является окружность с диаметром A^*B^*. Для этого достаточно показать, что РA^*M^*B^*  =  90°. Но согласно задаче 28.1 DOAM ~ DOM^*A^* и DOBM ~ DOM^*B^*, следовательно, РOMA = РOA^*M^* и РOMB = РOB^*M^*, точнее, Р(OM, MA) =  – Р(OA^*, M^*A^*) и Р(OM, MB)  =   – Р(OB^*, M^*B^*) (чтобы не рассматривать различные случаи расположения точек, мы воспользуемся свойствами ориентированных углов между прямыми, изложенными в гл. 2). Поэтому Р(A^*M^*, M^*B^*)  =  Р(A^*M^*, OA^*) + Р(OB^*, M^*B^*) = Р(OM, MA) + Р(MB, OM) = Р(MB, MA) = 90°.

28.4.

Если точка касания не совпадает с центром инверсии, то после инверсии эти окружности (окружность и прямая) будут по-прежнему иметь одну общую точку, т. е. касание сохранится.

28.5.

Проведем через точку пересечения окружностей касательные l₁ и l₂. Так как при инверсии касающиеся окружности и прямые переходят в касающиеся (см. задачу 28.4), то угол между образами окружностей равен углу между образами касательных к ним. При инверсии с центром O прямая l_i переходит в себя или в окружность, касательная к которой в точке O параллельна l_i. Поэтому угол между образами прямых l₁ и l₂ при инверсии с центром O равен углу между этими прямыми.

28.6.

Первое решение. Проведем через центры окружностей координатную ось. Пусть a₁ и a₂ - координаты точек пересечения оси с S₁, b₁ и b₂ - с S₂. Пусть O - точка на оси с координатой x. Тогда при инверсии с центром O и степенью k наши окружности перейдут в окружности, диаметры которых лежат на оси, и их концы имеют координаты a₁ў, a₂ў и b₁ў, b₂ў, где

a1ў = x +

k a1 – x

,

a2ў = x +

k a2 – x

,

b1ў = x +

k b1 – x

,

b2ў = x +

k b2 – x

. Полученные окружности концентричны, если (a₁ў + a₂ў)/2 = (b₁ў + b₂ў)/2, т. е.

1 a1 – x  +   1 a2 – x  =   1 b1 – x  +   1 b2 – x ,

откуда (b₁ + b₂ – a₁ – a₂)x² + 2(a₁a₂ – b₁b₂)x + b₁b₂(a₁ + a₂) – a₁a₂(b₁ + b₂) = 0. Дискриминант этого квадратного уравнения относительно x равен 4(b₁ – a₁)(b₁ – a₂)(b₂ – a₁)(b₂ – a₂). Он положителен в точности тогда, когда окружности не пересекаются, что и доказывает существование искомой инверсии.

Второе решение. Возьмем из прямой, соединяющей центры O₁ и O₂ окружностей, точку C так, чтобы касательные, проведенные к окружностям из точки C, были равны. Эту точку C можно построить, проведя радикальную ось окружностей (см. задачу 3.54). Пусть l - длина этих касательных. Окружность S радиуса l с центром в C перпендикулярна S₁ и S₂. Поэтому при инверсии с центром O, где O - любая из точек пересечения окружности S с прямой O₁O₂, S перейдет в прямую, перпендикулярную окружностям S₁^* и S₂^* и, следовательно, проходящую через их центры. Но прямая O₁O₂ тоже проходит через центры S₁^* и S₂^*, поэтому окружности S₁^* и S₂^* концентричны, т. е. O - центр искомой инверсии.

В случае, когда S₂ не окружность, а прямая, роль прямой O₁O₂ играет перпендикуляр, опущенный из точки O₁ на S₂, точка C будет точкой его пересечения с S₂, а l - длиной касательной, проведенной из C к S₁.

28.7.

Пусть точка A лежит вне S, тогда Aў лежит внутри S и РMAўN = (ИMN + ИMўNў)/2 = ИMN = РMON, т. е. четырехугольник MNOAў вписанный. Но при инверсии относительно S прямая MN перейдет в окружность, проходящую через точки M, N, O (задача 28.2). Поэтому точка A^* (образ A при инверсии) лежит на описанной окружности четырехугольника MNOAў. По тем же причинам точки Aў и A^* принадлежат и окружности, проходящей через Mў, Nў и O. Но эти две окружности не могут иметь других общих точек, кроме O и Aў. Следовательно, A^* = Aў.

В случае, когда A лежит внутри S, применим уже доказанное к прямой MNў и точке Aў (она находится вне S). Получим, что A = (Aў)^*. Но тогда Aў = A^*.

28.8.

Пусть точка A лежит вне окружности S. Проведем через A прямую, касающуюся S в точке M. Пусть MAў — высота треугольника OMA. Прямоугольные треугольники OMA и OAўM подобны, поэтому AўO : OM = OM : OA и OAў = R²/OA, т. е. точка Aў искомая. Если же A находится внутри S, то выполним построение в обратном порядке: проводим перпендикуляр AM к OA (точка M лежит на окружности). Тогда касательная к S в точке M пересекается с лучом OA в искомой точке A^*. Доказательство повторяется дословно.

28.9.

Если обе данные точки A и B лежат на данной окружности S (или прямой), то задача решений не имеет. Пусть теперь точка A не лежит на S. При инверсии с центром A искомая окружность перейдет в прямую, проходящую через B^* и касающуюся S^*. Из этого вытекает следующее построение. Сделаем инверсию относительно произвольной окружности с центром A. Проведем через B^* касательную l к S^*. Еще раз сделаем инверсию. Тогда l перейдет в искомую окружность.

28.10.

После инверсии с центром в данной точке окружности S₁ и S₂ перейдут в пару окружностей S₁^* и S₂^* (окружность S^* и прямую l; пару прямых l₁ и l₂), а касающаяся их окружность - в общую касательную к S₁^* и S₂^* (соответственно в касательную к S^*, параллельную l; прямую, параллельную l₁ и l₂). Поэтому для построения искомой окружности нужно построить прямую, касающуюся S₁^* и S₂^* (касающуюся S^* и параллельную l; параллельную l₁ и l₂), и еще раз сделать инверсию.

28.11.

Сведем эту задачу к задаче 28.10. Пусть окружность S радиуса r касается окружностей S₁, S₂, S₃ радиусов r₁, r₂, r₃ соответственно. Касание окружности S с каждой из S_i (i = 1, 2, 3) может быть как внешним, так и внутренним, поэтому всего возможно восемь различных случаев касания. Пусть, например, S касается S₁ и S₃ внешним, а S₂ - внутренним образом (рис. 28.7). Заменим окружности S, S₂, S₃ на концентрические им окружности Sў, S₂ў, S₃ў так, чтобы Sў касалась S₂ў и S₃ў и проходила через центр O₁ окружности S₁. Для этого достаточно, чтобы радиусы Sў, S₂ў, S₃ў равнялись r + r₁, r₂ + r₁, |r₃ – r₁|. Обратно, по окружности Sў, проходящей

Рис. 28.7

через O₁ и касающейся S₂ў и S₃ў (внешне, если r₃ – r₁ і 0, и внутренне, если r₃ – r₁ < 0), мы можем построить окружность S, дающую решение задачи, уменьшив радиус Sў на r₁. Построение такой окружности Sў описано в решении задачи 28.10 (если виды касания заданы, то окружность строится однозначно). Таким же способом можно выполнить построение и в остальных возможных вариантах касания.

28.12.

При инверсии с центром в данной точке A искомая окружность перейдет в прямую, перпендикулярную образам данных окружностей S₁ и S₂, т. е. в прямую, соединяющую центры S₁^* и S₂^*. Таким образом, искомая окружность - образ при этой инверсии произвольной прямой, проходящей через центры S₁^* и S₂^*.

28.13.

Сделаем инверсию, переводящую окружности S₁ и S₂ в пару прямых (если они имеют общую точку) или в пару концентрических окружностей (см. задачу 28.6) с общим центром A. В последнем случае окружность, перпендикулярная им обеим, перейдет в прямую, проходящую через A (так как не существует окружностей, перпендикулярных двум концентрическим окружностям); касательная, проведенная из A к S^*, есть образ искомой окружности при этой инверсии. Если S₁^* и S₂^* - параллельные прямые, то образ искомой окружности - любая из двух прямых, перпендикулярных S₁^* и S₂^* и касающихся S^*. Наконец, если S₁^* и S₂^* - пересекающиеся в некоторой точке B прямые, то искомая окружность - это образ при инверсии любой из двух окружностей с центром B, касающихся S^*.

28.14.

После инверсии с центром в точке A задача сводится к построению прямой l, проходящей через B^*, пересекающей окружность S^* под углом a, т. е. к построению точки X на S^* такой, что РB^*XO = 90° – a, где O - центр S^*. Эта точка лежит на пересечении S^* с дугой, из которой отрезок B^*O виден под углом 90° – a.

28.15.

а) Пусть AB - данный отрезок. Проведем окружность с центром B радиуса AB. Отложив на этой окружности хорды AX, XY и YZ, равные по длине AB, мы получим равносторонние треугольники ABX, XBY и YBZ. Поэтому РABZ = 180° и AZ = 2AB.

28.16.

Проведем окружности с центрами B и C, проходящие через A. Тогда отличная от A точка пересечения этих окружностей и будет искомой.

28.17.

Предположим сначала, что точка A лежит вне окружности S. Пусть B и C - точки пересечения S и окружности радиуса AO с центром A. Проведем окружности с центрами B и C радиуса BO = CO; пусть O и Aў - их точки пересечения. Докажем, что Aў - искомая точка. Действительно, при симметрии относительно прямой OA окружности с центрами B и C переходят друг в друга, поэтому точка Aў остается на месте. Следовательно, точка Aў лежит на прямой OA. Равнобедренные треугольники OAB и OBAў подобны, так как имеют равные углы при основании. Следовательно, OAў : OB = OB : OA или OAў = OB²/OA, что и требовалось.

28.18.

Пусть A и B - данные точки. Если точка C лежит на луче AB и AC = 2AB, то при инверсии относительно окружности радиуса AB с центром A точка C перейдет в середину отрезка AB. Построение сведено к задачам 28.15, а) и 28.17.

28.19.

Центром этой окружности является образ при инверсии точки Oў, симметричной O относительно AB. Остается применить задачи 28.16 и 28.17.

28.20.

Пусть A, B, C - данные точки. Построим (задача 28.17) образы точек B и C при инверсии с центром A и произвольной степенью. Тогда окружность, проходящая через A, B и C, будет образом прямой B^*C^* при этой инверсии, и ее центр строится по предыдущей задаче.

28.21.

а) Пользуясь предыдущей задачей, построим центр O окружности S. Затем построим точки A^* и B^* - образы точек A и B при инверсии относительно S. Образ прямой AB является окружностью S₁, проходящей через точки A^*, B^* и O. Воспользовавшись задачей 28.19, построим S₁. Искомые точки являются образами точек пересечения окружностей S и S₁, т. е. просто точками пересечения S и S₁.

28.22.

При инверсии с центром в вершине A сегмента конфигурация, изображенная на рис. 28.1, перейдет в пару касающихся окружностей, вписанных в угол с вершиной B^*. Ясно, что множество точек касания таких окружностей - это биссектриса угла, а искомое множество является ее образом при инверсии - дугой окружности с концами AB, делящей пополам угол между дугой сегмента и хордой AB.

Рис. 28.8 Рис. 28.9

28.24. Данная инверсия переводит прямую BC в окружность, проходящую через точки A, B и C, причем образ отрезка BC должен остаться внутри угла BAC.

28.25. Пусть S₁ и S₂ - окружности, вписанные в сегмент; M, N - их точки пересечения (рис. 28.9). Покажем, что прямая MN проходит через точку P окружности сегмента, равноудаленную от его концов A и B. Действительно, согласно предыдущей задаче инверсия с  центром P и степенью PA² переводит отрезок AB в дугу AB, а окружности S₁ и S₂ - в окружности S₁^* и S₂^*, по-прежнему вписанные в сегмент. Но касательные к S₁, проведенные из P, касаются также и S₁^*, поэтому S₁^* = S₁ (так как обе эти окружности одинаковым образом касаются трех фиксированных прямых). Аналогично S₂^* = S₂, следовательно, точки M и N меняются местами при инверсии, т. е. M^* = N и прямая MN проходит через центр инверсии.

28.26.

Сделаем инверсию с центром A. Интересующие нас углы будут равны тогда (см. задачу 28.5) соответственно углу между прямыми B^*C^* и B^*D^* и углу между прямой C^*D^* и описанной окружностью треугольника B^*C^*D^*. Оба этих угла равны половине дуги C^*D^*.

28.27.

Сделав инверсию с центром A, мы получим три прямые, проходящие через B: прямые S₁^* и S₂^* касаются окружности S^*, а S₃^* ей перпендикулярна. Таким образом, прямая S₃^* проходит через центр S^* и является биссектрисой угла, образованного S₁^* и S₂^*. Следовательно, окружность S₃ делит пополам угол между S₁ и S₂.

28.28.

Из условия на типы касания следует, что после инверсии с центром A мы получим две окружности, вписанные в один и тот же угол или в пару вертикальных углов. В любом случае окружности S₁^* и S₂^* переводятся одна в другую гомотетией с центром A. Эта гомотетия переводит один отрезок, соединяющий точки касания, в другой. Поэтому прямые B₁^*C₁^* и B₂^*C₂^* параллельны, а их образы при инверсии касаются в точке A.

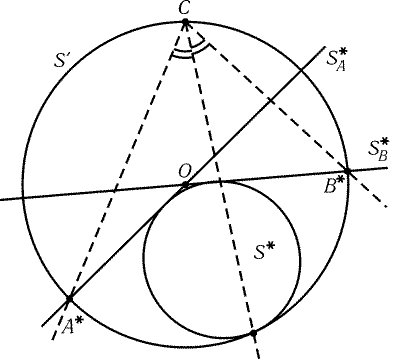
Рис. 28.10

28.29. Сделаем инверсию с центром C, при которой прямая AB переходит в окружность Sў, проходящую через точку пересечения окружностей S_A и S_B (отличную от точки C). При такой инверсии окружности S_A и S_B переходят в прямые, проходящие через центр O окружности Sў (рис. 28.10). Ясно, что окружность S^* касается окружности Sў в середине дуги A^*B^*.

                      28.30. а) Пусть A₁, B₁ и C₁ - середины сторон BC, CA и AB. Докажем, например, что описанная окружность треугольника A₁B₁C₁ касается вписанной окружности S и вневписанной окружности S_a, касающейся стороны BC. Пусть точки Bў и Cў симметричны B и C относительно биссектрисы угла A (т. е. BўCў - вторая общая внутренняя касательная к S и S_a), P и Q - точки касания окружностей S и S_a со стороной BC, D и E - точки пересечения прямых A₁B₁ и A₁C₁ с прямой BўCў. Согласно задаче 3.2 BQ = CP = p – c, а значит, A₁P = A₁Q = |b – c|/2. Достаточно доказать, что при инверсии с центром A₁ и  степенью A₁P² точки B₁ и C₁ переходят в D и E (при этой инверсии окружности S и S_a переходят в себя, а описанная окружность треугольника A₁B₁C₁ переходит в  прямую BўCў).

Пусть K - середина отрезка CCў. Точка K лежит на прямой A₁B₁, причем A₁K = BCў/2 = |b – c|/2 = A₁P. Кроме того, A₁D : A₁K = BCў : BA = A₁K : A₁B₁, т. е. A₁D · A₁B₁ = A₁K² = A₁P². Аналогично A₁E · A₁C₁ = A₁P².

б) Окружность Sў, проходящая через середины сторон треугольника ABC, проходит еще и через основания высот (задача 5.117). Пусть H - основание высоты, опущенной из вершины B, B₂ - середина стороны AC. Достаточно проверить, что инверсия с центром A и степенью

AB2 · AH =

b 2

ccos A = prctg A

переводит вневписанную окружность S_a во вписанную окружность треугольника AB₁C₁. Действительно, эта инверсия переводит окружность Sў в себя, а согласно задаче а) окружности Sў и S_a касаются.

Пусть X - середина отрезка AB₁. Тогда CX = r и AX = rctg  A. Остается заметить, что длина касательной из точки A к окружности S_a равна p.

28.31.

После инверсии с центром в точке пересечения S₁ и S₂ получим прямые l₁, l₂ и l, пересекающиеся в одной точке. Прямая l₁ пересекает окружность S₄^* в точках A и B, прямая l₂ пересекает S₃^* в точках C и D, а прямая l проходит через точки пересечения этих окружностей. Поэтому точки A, B, C, D лежат на одной окружности (задача 3.9).

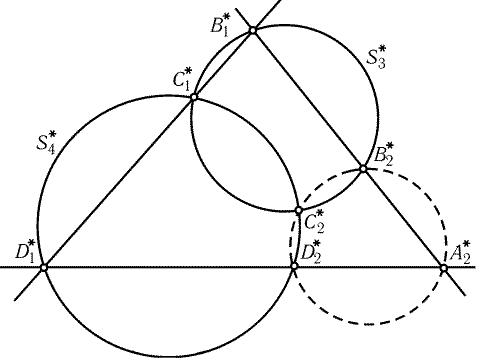
Рис. 28.11

28.32. Сделаем инверсию с центром в точке A₁. Тогда окружности S₁, S₂ и S₄ перейдут в прямые A₂^*D₁^*, B₁^*A₂^* и  D₁^*B₁^*, окружности S₃ и S₄ — в окружности S₃^* и S₄^*, описанные около треугольников B₂^*C₁^*B₁^* и C₁^*D₁^*D₂^* (рис. 28.11). Проведем окружность через точки B₂^*, D₂^*, A₂^*. Согласно задаче 2.81, а) она пройдет через точку C₂^* пересечения окружностей S₃^* и S₄^*. Таким образом, точки A₂^*, B₂^*, C₂^*, D₂^* лежат на одной окружности. Следовательно, точки A₂, B₂, C₂, D₂ лежат на одной окружности или прямой.

28.33. Пусть P, Q, R, S, T - точки пересечения окружностей S₁, S₂, S₃, S₄, S₅, о которых говорится в условии (см. рис. 28.4). Докажем, например, что точки P, Q, R, S лежат на одной окружности. Проведем окружность S, описанную около треугольника NKD. Применяя результат задачи 2.85, а) (совпадающей с 19.46) к  четырехугольникам AKDE и BNDC, получаем, что окружности S₄, S₅ и S пересекаются в одной точке (в точке P) и  окружности S₂, S₃, S тоже пересекаются в одной точке (в  точке S). Следовательно, окружность S проходит через точки P и S. Заметим теперь, что из восьми точек пересечения окружностей S, S₁, S₂, S₅ четыре, а именно N, A, B, K лежат на одной прямой. Следовательно, согласно задаче 28.32 оставшиеся четыре точки P, Q, R, S лежат на одной окружности.

28.34.

После инверсии с центром в точке пересечения описанных окружностей треугольников A₁A₂B₃, A₁B₂A₃ и B₁A₂A₃ эти окружности перейдут в прямые, а утверждение задачи сведется к доказательству того, что описанные окружности треугольников B₁^*B₂^*A₃^*, B₁^*A₂^*B₃^* и A₁^*B₂^*B₃^* проходят через одну точку, т. е. к утверждению задачи 2.81, а).

28.35.

После инверсии с центром в точке пересечения описанных окружностей треугольников A₁B₁C₁, A₁B₂C₂, A₂B₁C₂ и A₂B₂C₁ мы получим четыре прямые и четыре окружности, описанные около образованных этими прямыми треугольников. Согласно задаче 2.85, а) эти окружности проходят через одну точку.

28.36.

а) Обозначим через M_ij точку пересечения прямых l_i и l_j, а через S_ij - окружность, соответствующую трем оставшимся прямым. Тогда точка A₁ является отличной от точки M₃₄ точкой пересечения окружностей S₁₅ и S₁₂.

Повторив это рассуждение для всех точек A_i, получаем, что они в силу задачи 28.33 лежат на одной окружности.

б) Докажем утверждение задачи по индукции, рассматривая отдельно случай четного и нечетного n.

Пусть n нечетно. Обозначим через A_i точку, соответствующую набору из n – 1 прямой, получаемому отбрасыванием прямой l_i, а через A_ijk - точку, соответствующую набору из n данных прямых без прямых l_i, l_j и l_k. Аналогично обозначим через S_ij и S_ijkm окружности, соответствующие наборам из n – 2 и n – 4 прямых, получаемых отбрасыванием прямых l_i, l_j и l_i, l_j, l_k, l_m.

Для того чтобы доказать, что n точек A₁, A₂, ј, A_n лежат на одной окружности, достаточно доказать, что любые четыре из них лежат на одной окружности. Докажем это, например, для точек A₁, A₂, A₃ и A₄. Так как точки A_i и A_ijk лежат на S_ij, то окружности S₁₂ и S₂₃ пересекаются в точках A₂ и A₁₂₃, окружности S₂₃ и S₃₄ - в точках A₃ и A₂₃₄, окружности S₃₄ и S₄₁ - в точках A₄ и A₁₃₄, окружности S₄₁ и S₁₂ - в точках A₁ и A₁₂₄. Но точки A₁₂₃, A₂₃₄, A₁₃₄ и A₁₂₄ лежат на одной окружности - окружности S₁₂₃₄, поэтому согласно задаче 28.32 точки A₁, A₂, A₃ и A₄ лежат на одной окружности.

Пусть теперь n четно; S_i, A_ij, S_ijk, A_ijkm - окружности и точки, соответствующие наборам из n – 1, n – 2, n – 3 и n – 4 прямых. Для того чтобы доказать, что окружности S₁, S₂, ј, S_n пересекаются в одной точке, покажем, что это верно для любых трех из них. (Этого достаточно при n і 5; см. задачу 26.12.) Докажем, например, что S₁, S₂ и S₃ пересекаются в одной точке. По определению точек A_ij и окружностей S_i и S_ijk точки A₁₂, A₁₃ и A₁₄ лежат на окружности S₁; A₁₂, A₂₃ и A₂₄ - на S₂; A₁₃, A₁₄ и A₃₄ - на S₃; A₁₂, A₁₄ и A₂₄ - на S₁₂₄; A₁₃, A₁₄, A₃₄ - на S₁₃₄; A₂₃, A₂₄, A₃₄ - на S₂₃₄. Но три окружности S₁₂₄, S₁₃₄ и S₂₃₄ проходят через точку A₁₂₃₄ поэтому согласно задаче 28.34 и окружности S₁, S₂ и S₃ пересекаются в одной точке.

28.37.

а) Обозначим через M_ij точку пересечения прямых l_i и l_j. Тогда точка A₁, соответствующая тройке l₂, l₃, l₄, - это точка пересечения описанных окружностей треугольников M₂M₃M₂₃ и M₃M₄M₃₄. Рассуждая аналогично для точек A₂, A₃ и A₄, мы получим, что точки A₁, A₂, A₃ и A₄ лежат на одной окружности согласно задаче 28.32, так как точки M₁, M₂, M₃, M₄ лежат на одной окружности.

Пусть n четно и A_i, S_ij, A_ijk и S_ijkm обозначают точки и окружности, соответствующие наборам из n – 1, n – 2, n – 3 и n – 4 прямых. Докажем, что точки A₁, A₂, A₃, A₄ лежат на одной окружности. По определению точек A_i и A_ijk окружности S₁₂ и S₂₃ пересекаются в точках A₂ и A₁₂₃; S₂₃ и S₃₄ - в точках A₃ и A₂₃₄; S₃₄ и S₄₁ - в точках A₄ и A₁₃₄; S₄₁ и S₁₂ - в точках A₁ и A₁₂₄. Точки A₁₂₃, A₂₃₄, A₁₃₄ и A₁₂₄ лежат на окружности S₁₂₃₄, поэтому согласно задаче 28.32 точки A₁, A₂, A₃, A₄ лежат на одной окружности. Аналогично доказывается, что и любые четыре из точек A_i (и, следовательно, все они) лежат на одной окружности.

Доказательство в случае нечетного n і 5 дословно повторяет доказательство утверждения задачи 28.36, б) для случая четного n.

28.38.

Если окружности R₁ и R₂ пересекаются или касаются, то инверсия с центром в их точке пересечения переведет окружности S₁, S₂, ј, S_n в окружности, касающиеся пары прямых и друг друга в точках A₁^*, A₂^*, ј, A_n – 1^*, лежащих на биссектрисе угла, образованного прямыми R₁^* и R₂^*, если R₁^* и R₂^* пересекаются, и на прямой, параллельной R₁^* и R₂^*, если эти прямые не пересекаются. Применив инверсию еще раз, получим, что точки A₁^*, A₂^*, ј, A_n – 1^* лежат на одной окружности.

28.39.

Сделаем инверсию, переводящую R₁ и R₂ в пару концентрических окружностей. Тогда окружности S₁^*, S₂^*, ј, S_n^* и T₁^* равны между собой (рис. 28.12). Повернув цепочку S₁^*, ј, S_n^* вокруг центра окружности R₁^* так, чтобы S₁^* перешла в T₁^*, и сделав инверсию еще раз, получим нужную цепочку T₁, T₂, ј, T_n.

Рис. 28.12

28.40.

Центр инверсии, переводящей окружности R₁ и R₂ в концентрические, лежит (см. решение задачи 28.6) на линии их центров. Поэтому, сделав эту инверсию и учтя, что угол между окружностями и касание при этом сохраняется, мы сведем доказательство к случаю концентрических окружностей R₁ и R₂ с центром O и радиусами r₁ и r₂.

Проведем окружность S с центром P радиуса (r₁ – r₂)/2, касающуюся R₁ изнутри и R₂ внешне, и две окружности Sў и Sўў радиуса (r₁ + r₂)/2 с центрами A и B, касающиеся R₁ и R₂ в их точках пересечения с прямой OP (рис. 28.13). Пусть OM и ON - касательные к S, проведенные из O. Очевидно, что цепочка из n окружностей, касающихся R₁ и R₂, существует тогда и  только тогда, когда угол MON равен m 360°/n (в этом случае окружности цепочки m раз обегают окружность R₂). Поэтому осталось доказать, что угол между окружностями Sў и Sўў равен РMON. Но угол между Sў и Sўў равен углу между их радиусами, проведенными в точку пересечения C. Кроме того, DACO = DPON (так как OP = r₁ – (r₁ – r₂)/2 = (r₁ + r₂)/2  =  AC, PN = (r₁ – r₂)/2 = r₁ – ((r₁ + r₂)/2) = OA, РPNO = РAOC  =  90°). Поэтому РACB = 2РACO = 2РPON = РNOM.

Рис. 28.13 Рис. 28.14

28.41.

Пусть R₁ и R₂ - какая¯либо пара несоприкасающихся окружностей. Оставшиеся четыре окружности образуют цепочку, поэтому по предыдущей задаче окружности Sў и Sўў, касающиеся R₁ и R₂ в точках их пересечения с линией центров, пересекаются под прямым углом (рис. 28.14). Если R₂ лежит внутри R₁, то радиусы rў и rўў окружностей Sў и Sўў равны (r₁ + r₂ + d)/2 и  (r₁ + r₂ – d)/2, а расстояние между их центрами dў = 2r₁ – r₁ – r₂  =  r₁ – r₂. Угол между Sў и Sўў равен углу между их радиусами, проведенными в точку пересечения, поэтому (dў)² = (rў)² + (rўў)² или, после преобразований, d² = r₁² + r₂² – 6r₁r₂.

Глава 28. § -1  |	Оглавление |	Глава 29.

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.