| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
29.1.
-
Нам надо доказать, что если Aў, Bў, Cў - образы точек A,
B, C при растяжении относительно прямой l с коэффициентом k
и точка C лежит на прямой AB, то точка Cў лежит на прямой
AўBў. Пусть
. Обозначим через A1, B1, C1
проекции точек A, B, C на прямую l, и пусть
,
,
,
,
,
,
,
. Из того, что при проекции на прямую l
сохраняется отношение длин пропорциональных векторов, следует, что
y = tx и y + (c – a) = t(y + (b – a)).
Вычитая первое равенство из второго, получаем (c – a) = t(b – a). По определению растяжения aў = ka,
bў = kb, cў = kc, поэтому
|
®
AўCў
|
= y + k(c – a) = tx + k(t(b – a)) = t(x + k(b – a)) = t |
®
AўBў
|
|
.
-
29.2.
-
По определению образы прямых - прямые, а из взаимной
однозначности аффинного преобразования следует, что образы
непересекающихся прямых не пересекаются.
-
29.3.
-
Пусть
. Рассмотрим сначала случай, когда
точки A, B, C, D не лежат на одной прямой. Тогда ABCD
- параллелограмм. Из предыдущей задачи следует, что A1B1C1D1
- тоже параллелограмм, поэтому
Пусть теперь точки A, B, C, D лежат на одной прямой.
Возьмем такие точки E и F, не лежащие на этой прямой, что
. Пусть E1 и F1 - их образы.
Тогда
|
®
A1B1
|
= |
®
E1F1
|
= |
®
C1D1
| .
|
-
29.4.
-
a)
| L( |
®
0
|
) = L( |
®
AA
|
) = |
®
L(A)L(A)
|
= |
®
0
|
|
.
б)
| L( |
®
AB
|
+ |
®
BC
|
) = L( |
®
AC
|
) = |
®
L(A)L(C)
|
= |
®
L(A)L(B)
|
+ |
®
L(B)L(C)
|
= L( |
®
AB
|
) + L( |
®
BC
|
)
|
.
в) Предположим сначала, что число k целое. Тогда
|
L(ka) = L( |
a + · + a
k
|
) = |
L(a) + ј + L(a)
k
|
= kL(a). |
|
Пусть теперь k = m/n - рациональное число. Тогда
nL(ka) = L(nka) = L(ma) = mL(a), поэтому
L(ka) = mL(a)/n = kL(a). Наконец, если k -
любое действительное число, то всегда найдется последовательность kn
рациональных чисел, сходящаяся к k (например, последовательность
десятичных приближений k). Поскольку L непрерывно, то
| L(ka) = L( |
lim
n®Ґ
|
kna) = |
lim
n®Ґ
|
knL(a) = kL(a).
|
-
29.5.
-
В силу задачи 29.4, в) из условия
следует, что
| q |
®
AўCў
|
= qL( |
®
AC
|
) = L(q |
®
AC
|
) = L(p |
®
CB
|
) = pL( |
®
CB
|
) = p |
®
CўBў
|
|
.
-
29.6.
-
а) Зададим отображение L следующим образом. Пусть X -
произвольная точка. Поскольку e1, e2 - базис,
существуют однозначно определенные числа x1 и x2
такие, что
. Поставим в соответствие
точке X такую точку Xў = L(X), что
. Так как e1ў, e2ў - тоже базис,
полученное отображение взаимно однозначно. (Обратное отображение строится
аналогично.) Докажем, что любая прямая AB при отображении L
переходит в прямую. Пусть Aў = L(A), Bў = L(B) и a1, a2, b1,
b2 - координаты точек A и B в базисе e1, e2,
т. е. такие числа, что
,
. Рассмотрим произвольную
точку C прямой AB. Тогда
при некотором k,
т. е.
|
®
OC
|
= |
®
OA
|
+ k( |
®
OB
|
– |
®
OA
|
) = ((1 – k)a1 + kb1)e1 + ((1 – k)a2 + kb2)e2
|
. Следовательно, если Cў = L(C), то
|
®
OўCў
|
= ((1 – k)a1 + kb1)e1ў + ((1 – k)a2 + kb2)e2ў = |
®
OўAў
|
+ k( |
®
OўBў
|
– |
®
OўAў
|
)
|
, т. е. точка Cў лежит на
прямой AўBў.
Единственность отображения L следует из результата задачи 29.4.
В самом деле,
| L( |
®
OX
|
) = x1L(e1) + x2L(e2)
|
, т. е.
образ точки X однозначно определяется образами векторов e1,
e2 и точки O.
б) Для доказательства можно воспользоваться предыдущей задачей,
положив O = A,
,
,
Oў = A1,
,
.
в) Следует из задачи б) и из того. что параллельные прямые
переходят в параллельные.
-
29.7.
-
Пусть ABCDE - правильный пятиугольник. Согласно задаче
29.6, б) существует аффинное преобразование, которое три
последовательные вершины данного пятиугольника переводит в точки
A, B, C. Пусть Dў и Eў - образы остальных двух
вершин при этом преобразовании. Докажем, что они совпадают с D
и E.
С одной стороны, ADў|| BC и CEў|| AB, поэтому точка Dў
лежит на прямой AD, а точка Eў - на прямой CE. С другой
стороны, EўDў|| AC|| ED, поэтому если бы точки Dў и Eў не
совпадали с точками D и E, то либо они обе были бы вне
полосы, ограниченной прямыми AE и BD (рис. 29.1, а ), либо обе
внутри этой полосы (рис. 29.1, б ). В обоих случаях прямые AEў и
BDў не были бы параллельны.
-
29.8.
-
Пусть M и N - произвольные точки, не лежащие на прямой l.
Обозначим через M0 и N0 их проекции на прямую l, а через Mў
и Nў - образы точек M и N при отображении L.
Прямые M0M
и N0N параллельны, так как они обе перпендикулярны l, т. е.
существует такое число k, что
. Тогда
согласно задаче 29.4, в)
. Поэтому образ
треугольника M0MMў
при параллельном переносе на вектор
гомотетичен с коэффициентом k треугольнику N0NNў, следовательно,
прямые MMў и NNў параллельны.
-
29.9.
-
Поскольку аффинное отображение однозначно определяется
образами вершин любого фиксированного треугольника (см. задачу 29.6, б)),
достаточно доказать, что из любого треугольника можно
при помощи двух растяжений получить треугольник, подобный
некоторому наперед заданному, например, равнобедренный прямоугольный.
Докажем это. Пусть ABC - произвольный треугольник,
BN - биссектриса внешнего угла B, прилежащего к стороне BC.
Тогда при растяжении относительно BN с коэффициентом
tg 45°/tg РCBN из треугольника ABC получается
треугольник AўBўCў с прямым углом Bў. Из прямоугольного треугольника
при помощи растяжения относительно одного из его катетов всегда можно
получить равнобедренный прямоугольный треугольник.
-
29.10.
-
Докажем сначала, что если A1A2… An - правильный многоугольник,
вписанный в единичную окружность, а O - его центр, то указанные в условии
задачи равенства выполняются, т. е.
|
|
®
OAi – 1
|
+ |
®
OAi + 1
|
= 2k |
®
OAi
|
, i = 1,…,n |
| (1) |
(мы считаем, что A0 = An и An + 1 = A1; через k обозначено число
cos (2p/n)). Для этого при каждом фиксированном i выберем на плоскости
систему координат с центром в точке O и осью Ox, направленной вдоль луча
OAi. Тогда точки Ai – 1, Ai и Ai + 1 имеют координаты
, (1, 0) и
соответственно. Равенство (1) при данном i теперь легко проверяется.
В силу задачи 29.4 равенства (1) выполняются также для образа правильного
n-угольника при аффинном преобразовании.
Наоборот, пусть для многоугольника A1A2… An и точки O внутри его
выполнены равенства (1). Возьмем правильный многоугольник B1B2… Bn с
центром O и рассмотрим аффинное преобразование L, которое переводит
треугольник OB1B2 в треугольник OA1A2. Докажем индукцией по i, что
L(Bi) = Ai для всех i і 2. При i = 2 это утверждение следует из
определения отображения L. Предположим, что мы его доказали для всех чисел,
не превосходящих i, и докажем для i + 1. Так как для правильных
многоугольников равенства (1) уже доказаны, а для многоугольника
A1A2… An они выполнены по предположению, то
|
|
®
OAi + 1
|
= 2k |
®
OAi
|
– |
®
OAi – 1
|
= |
|
|
= 2kL( |
®
OBi
|
) – L( |
®
OBi – 1
|
) = L(2k |
®
OBi
|
– |
®
OBi – 1
|
) = L( |
®
OBi + 1
|
). |
|
-
29.11.
-
Пусть L - данное аффинное преобразование, O - произвольная
точка, T - сдвиг на вектор
, и пусть L1 = T°L.
Тогда O - неподвижная точка преобразования L1. Среди всех
точек единичной окружности с центром O выберем точку A, для которой
максимальна длина вектора
. Пусть H - поворотная
гомотетия с центром O, которая точку L1(A) переводит в точку A,
и пусть L2 = H°L1 = H°T°L. Тогда L2 есть аффинное
преобразование, которое оставляет на месте точки O и A, а
значит, согласно задаче 29.4, в), и все остальные точки прямой OA,
причем, в силу выбора точки A, для всех точек M имеем неравенство
.
Докажем (и из этого будет следовать утверждение задачи), что L2
- сжатие относительно прямой OA. Если преобразование L2
тождественно, то оно является сжатием с коэффициентом 1, поэтому
будем считать, что L2 не тождественно. Согласно задаче 29.11 все
прямые вида
, где M - произвольная точка не
на прямой OA, друг другу параллельны. Пусть
-
единичный вектор, перпендикулярный всем этим прямым. Тогда B
- неподвижная точка преобразования L2, так как иначе было бы
|
| |
®
OL2(B)
|
| = |
Ц
|
OB2 + BL2(B)2
|
> |OB|. |
|
Если B не лежит на прямой OA, то согласно задаче 29.6, б)
преобразование L2 тождественно. Если B лежит на прямой OA, то
все прямые вида ML2(M) перпендикулярны неподвижной прямой
преобразования L2. При помощи задачи 29.4, в) несложно показать,
что отображение, обладающее этим свойством, является растяжением
или сжатием.
-
29.12.
-
Докажем сначала, что аффинное преобразование L, переводящее
данную окружность в себя, переводит диаметрально противоположные
точки в диаметрально противоположные. Для этого заметим,
что касательная к окружности в точке A переходит в прямую, которая
в силу взаимной однозначности преобразования L пересекается
с окружностью в единственной точке L(A), т. е. является касательной
в точке L(A). Поэтому если касательные в точках A и B параллельны
(т. е. AB - диаметр), то касательные в точках L(A) и L(B) тоже
параллельны, т. е. L(A)L(B) - тоже диаметр.
Фиксируем какой-нибудь диаметр AB данной окружности. Поскольку
L(A)L(B) — тоже диаметр, то существует движение P,
являющееся поворотом или симметрией, которое переводит A
и B в L(A) и L(B), а каждую из дуг a и b, на
которые точки A и B делят данную окружность, - в образ
этой дуги при отображении L.
Докажем, что отображение F = P – 1°L является тождественным.
В самом деле, F(A) = A и F(B) = B, следовательно, все точки прямой
AB остаются неподвижными. Поэтому если X - произвольная точка
окружности, то касательная в точке X пересекает прямую AB там
же, где и касательная в точке Xў = F(X), так как точка пересечения
остается неподвижной. А поскольку X и Xў лежат на одной и той
же из двух дуг a или b, то точка X совпадает с точкой Xў.
Итак, P – 1°L = E, т. е. L = P.
-
29.13.
-
Пусть a1 и a2 - какие-нибудь две перпендикулярные прямые.
Поскольку аффинное преобразование сохраняет отношение длин
параллельных отрезков, то длины всех отрезков, параллельных одной
прямой, умножаются на один и тот же коэффициент. Обозначим
через k1 и k2 эти коэффициенты для прямых a1 и a2.
Пусть j - угол между образами этих прямых. Докажем, что данное
аффинное преобразование изменяет площади всех многоугольников
в k раз, где k = k1k2sin j.
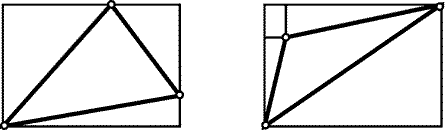
Рис. 29.2
Для прямоугольника со сторонами, параллельными a1 и a2,
а также для прямоугольного треугольника с катетами, параллельными a1
и a2, это утверждение очевидно. Любой другой треугольник можно
получить, отрезав от прямоугольника со сторонами, параллельными a1
и a2, несколько прямоугольных треугольников с катетами,
параллельными a1 и a2 (рис. 29.2), и, наконец, согласно
задаче 22.23, любой многоугольник можно разрезать на треугольники.
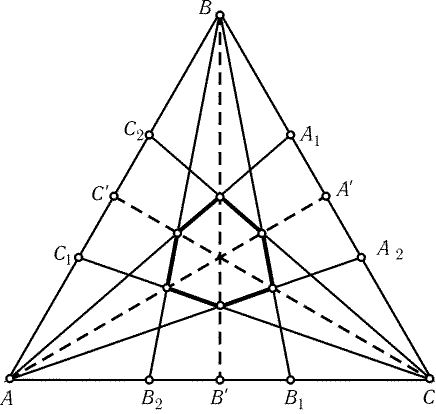
Рис. 29.3
29.14.
Поскольку аффинным преобразованием любой треугольник
переводится в правильный (задача 29.6, б)) и при этом сохраняются
отношения длин параллельных отрезков (задача 29.5), достаточно
доказать утверждение задачи для правильного треугольника ABC.
Пусть точки A1, A2, B1, B2, C1, C2 делят стороны
треугольника на равные части, а Aў, Bў, Cў - середины
сторон (рис. 29.3). При симметрии относительно AAў прямая BB1
перейдет в CC2, а прямая BB2 - в CC1. Поскольку
симметричные прямые пересекаются на оси симметрии, AAў содержит
диагональ рассматриваемого шестиугольника. Аналогично оставшиеся
диагонали лежат на BBў и CCў. Ясно, что медианы AAў, BBў, CCў
пересекаются в одной точке.
-
29.15.
-
Из задачи 29.6, б) следует, что любой параллелограмм
аффинным преобразованием можно перевести в квадрат. Поскольку
при этом сохраняются отношения длин параллельных отрезков
(задача 29.5), достаточно доказать утверждение задачи в случае,
когда ABCD - квадрат. Обозначим через P точку пересечения
прямых b и d. Нам достаточно доказать, что PC||MK. Отрезок
KL переходит в LM при повороте на 90° вокруг центра
квадрата ABCD, поэтому прямые b и d, которые соответственно
параллельны этим отрезкам, перпендикулярны; значит, P лежит на
окружности, описанной вокруг ABCD. Тогда РCPD = РCBD = 45°, следовательно, угол между прямыми CP и b равен
45°, но угол между прямыми MK и KL тоже равен 45°,
и b||KL, следовательно, CP||MK.
-
29.16.
-
а) Рассмотрим аффинное преобразование, переводящее треугольник ABC
в правильный треугольник AўBўCў. Пусть Oў, Mў, Nў, Pў -
образы точек O, M, N, P. При повороте на 120° вокруг
точки Oў треугольник MўNўPў переходит в себя, поэтому этот
треугольник правильный и Oў - точка пересечения его медиан.
Поскольку при аффинном преобразовании медиана переходит в медиану,
O - точка пересечения медиан треугольника MNP.
б) Решение аналогично решению предыдущей задачи.
-
29.17.
-
Рассмотрим аффинное преобразование, переводящее ABCD
в равнобедренную трапецию AўBўCўDў. В качестве такого преобразования
можно взять аффинное преобразование, переводящее
треугольник ADE в равнобедренный треугольник (E - точка
пересечения прямых AB и CD). Тогда при симметрии относительно
серединного перпендикуляра к AўDў точка Pў переходит в точку Qў,
т. е. прямые PўQў и AўDў параллельны.
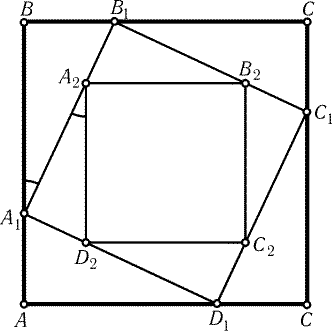
Рис. 29.4
29.18.
Любой параллелограмм ABCD аффинным преобразованием
можно перевести в квадрат (для этого нужно треугольник ABC
перевести в равнобедренный прямоугольный треугольник). Поскольку
в задаче идет речь только о параллельности прямых и об отношениях
отрезков, лежащих на одной прямой, можно считать, что ABCD -
квадрат. Рассмотрим поворот на 90°, переводящий ABCD в себя.
При этом повороте четырехугольники A1B1C1D1 и
A2B2C2D2 тоже переходят в себя, следовательно, они тоже являются
квадратами. При этом tg BA1B1 = BB1 : BA1 = A1D2 : A1A2 = tg A1A2D2, т. е. AB||A2D2 (рис. 29.4).
29.19.
а) Поскольку любой треугольник аффинным преобразованием переводится
в правильный и при этом середины сторон переходят в середины сторон,
центрально симметричные точки - в центрально симметричные, а
равновеликие треугольники - в равновеликие треугольники
(задача 29.13), то будем считать, что треугольник ABC равносторонний
со стороной a. Обозначим длины отрезков AM, BN, CP через p,
q, r соответственно. Тогда
|
SABC – SMNP = SAMP + SBMN + SCNP = |
|
|
= sin 60°(p(a – r) + q(a – p) + r(a – q))/2 = sin 60°(a(p + q + r) – (pq + qr + rp))/2. |
|
Аналогично
|
= sin 60°(r(a – p) + p(a – q) + q(a – r))/2 = sin 60°(a(p + q + r) – (pq + qr + rp))/2. |
|
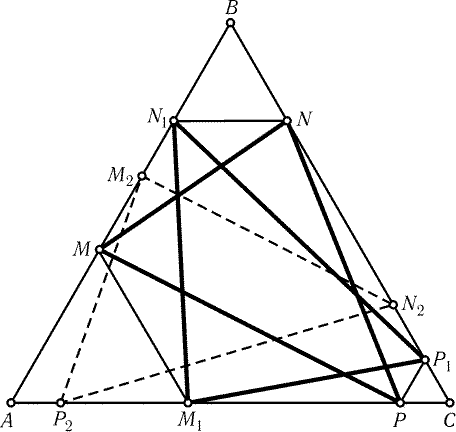
Рис. 29.5
б) Как и в предыдущей задаче, будем считать, что ABC -
правильный треугольник. Пусть M2N2P2 - образ треугольника
M1N1P1 при повороте вокруг центра треугольника ABC на
120° в направлении от A к B (рис. 29.5). Тогда
AM2 = CM1 = BM. Аналогично, BN2 = CN и CP2 = AP, т. е.
точки M2, N2, P2 симметричны точкам M, N, P
относительно середин соответствующих сторон. Тем самым задача
свелась к предыдущей.
29.20.
Пусть A = a/|a|, B = b/|b|, C = c/|c|, D = d/|d|. Эти точки
лежат на единичной окружности. Существует такой поворот
Ra, что B = Ra(A) и D = Ra(C). Но
Ra - это умножение на комплексное число
w = cos a + isin a. Следовательно, B/A = C/D = w. Пусть
k = |abcd|. Тогда
| ac |
-
b
|
|
-
d
|
= kAC |
-
B
|
|
-
D
|
= kAC |
-
B
|
– 1
|
|
-
D
|
– 1
|
= k
|
.
-
29.21.
-
Сдвинем данные треугольники на векторы – a и – aў
соответственно. В результате получатся собственно подобные
треугольники с вершинами 0, b – a, c – a и 0, bў – aў,
cў – aў. При этом точка b – a переводится в точку c – a той же
поворотной гомотетией, которой точка bў – aў переводится в точку
cў – aў. Из этого следует утверждение задачи.
-
29.22.
-
Если треугольники abc и aўbўcў собственно подобны, то
aў = az + w, bў = bz + w, cў = cz + w, где z и w - некоторые комплексные
числа. В таком случае
|
aў(b – c) + bў(c – a) + cў(a – b) = (az + w)(b – c) + (bz + w)(c – a) + (cz + w)(a – b) = 0. |
|
Предположим теперь, что
|
aў(b – c) + bў(c – a) + cў(a – b) = 0. |
| (1) |
Пусть
и
. Тогда aў = az + w и
bў = bz + w. Рассмотрим комплексное число cўў = cz + w. Треугольники abc и
aўbўcўў собственно подобны, поэтому
|
aў(b – c) + bў(c – a) + cўў(a – b) = 0. |
| (2) |
Из равенств (1) и (2) следует, что cўў = cў.
-
29.23.
-
Пусть v = (a + b)/2 - середина отрезка ab. Тогда прямоугольные треугольники
0au и 0vb собственно подобны, поскольку имеют равные углы в вершине 0.
Поэтому согласно задаче 29.21 a/u = v/b. Значит, u = ab/v = 2ab/(a + b).
-
29.24.
-
Прямоугольные треугольники, образованные соответственно точками
0,
, t и 0,
, t, собственно подобны.
Согласно задаче 29.21
т. е.
|
-
a
|
t – 1 + |
-
b
|
(t – a) = t |
-
a
|
– ta
|
(здесь мы воспользовались равенством
). Значит,
.
-
29.25.
-
Обозначим через A3 (соответственно B3, C3) отличную от
A2 (соответственно B2, C2) точку пересечения прямой
A1A2 (соответственно B1B2, C1C2) со вписанной
окружностью. Нужно доказать, что эти три точки совпадают.
Расположим треугольник ABC на комплексной плоскости так, чтобы вписанная
окружность совпала с единичной окружностью с центром в нуле, а прямая l - с
вещественной осью. Пусть a, b, c - точки касания вписанной окружности
со сторонами BC, CA, AB соответственно. Тогда согласно
задаче 29.23 A = 2bc/(b + c). Поэтому
| A1 = |
Re
| A = (A + |
-
A
|
)/2 = bc/(b + c) + |
-
b
|
|
-
c
|
/( |
-
b
|
+ |
-
c
|
)
|
. Но
Значит, A1 = bc/(b + c) + 1/(b + c) = (1 + bc)/(b + c). Ясно, что A2 = – a. Поэтому
согласно задаче 29.24
|
A3 = |
|
= |
a + b + c + abc
1 + ab + bc + ca
|
. |
|
Аналогично доказывается, что B3 и C3 тоже равны этому комплексному числу.
-
29.26.
-
а) Окружности и прямые задаются уравнениями
|
A(x2 + y2) + Bx + Cy + D = 0. |
|
с вещественными коэффициентами A, B, C, D (при A = 0
такое уравнение задает прямую, а при A № 0 - окружность,
точку или пустое множество). Наоборот, любое такое уравнение
задает либо окружность, либо прямую, либо точку, либо пустое
множество. Но z = x + iy, поэтому
и
, где c = (B – Ci)/2.
б) Образом числа z при инверсии с центром в нуле и степенью 1 является число
. Поделив уравнение из задачи а) на
, получим, что если
w - образ точки z при этой инверсии, то
|
Dw |
-
w
|
+ cw + |
-
c
|
|
-
w
|
+ A = 0, |
|
т. е. число w удовлетворяет уравнению того же вида.
-
29.27.
-
Установим соответствие между точками плоскости и комплексными числами так,
чтобы центр инверсии находился в нуле. Тогда образом числа z при инверсии со
степенью R является число
. Двойным отношением комплексных
чисел a, b, c, d называют комплексное число
|
(abcd) = |
a – c
a – d
|
: |
b – c
b – d
|
. |
|
Если a*, b*, c*, d* - образы чисел a, b, c, d при
инверсии, то
|
|
(a*b*c*d*)
|
= |
R/a – R/c
R/a – R/d
|
: |
R/b – R/c
R/b – R/d
|
= |
|
|
= |
R(c – a)/ac
R(d – a)/ad
|
: |
R(c – b)/bc
R(d – b)/bd
|
= |
a – c
a – d
|
: |
b – c
b – d
|
= (abcd). |
|
Задача а) следует из равенства модулей этих чисел, а задача б) - из равенства
их аргументов.
-
29.28.
-
а) Пусть A, B, C - точки, соответствующие числам a, b, c.
Комплексное число (a – b):(a – c) вещественно тогда и только тогда, когда векторы
и
пропорциональны.
б) Пусть S - окружность (или прямая), на которой лежат точки b, c, d.
Прибавив, если нужно, ко всем четырем числам одно и то же комплексное число
(это не изменяет двойное отношение), можно считать, что окружность S проходит
через 0. Значит, ее образ при инверсии - прямая. В решении
задачи 29.27 показано, что двойное отношение сохраняется при инверсии.
Поэтому остается решить такую задачу. Точки (т. е. комплексные числа) b, c,
d лежат на одной прямой; нужно доказать, что число a лежит на той же прямой
тогда и только тогда, когда число
|
a – c
a – d
|
: |
b – c
b – d
|
|
вещественно. Это следует из задачи а).
-
29.29.
-
а) Утверждение задачи вытекает из следующих свойств комплексных чисел:
1) |zw| = |z| · |w|; 2) |z + w| Ј |z| + |w|. Действительно, если
a, b, c, d - произвольные комплексные числа, то
|
(a – b)(c – d) + (b – c)(a – d) = (a – c)(b – d). |
|
Поэтому
|
|a – b| · |c – d| + |b – c| · |a – d| і |a – c| · |b – d|. |
|
б) Нужно лишь проверить соответствующее тождество для комплексных чисел a1,
…, a6 (это тождество получается из написанного в условии неравенства
заменой знака Ј на знак = , и заменой каждого сомножителя AiAj на
сомножитель (ai – aj).
в) Нестрогое неравенство |z + w| Ј |z| + |w| обращается в равенство тогда и
только тогда, когда комплексные числа z и w пропорциональны с вещественным
положительным коэффициентом пропорциональности. Поэтому, как видно из решения
задачи а), неравенство Птолемея обращается в равенство тогда и только тогда,
когда число
|
(a – b)(c – d)
(b – c)(a – d)
|
|
вещественно и положительно, т. е.
число
| q = |
a – b
a – d
|
: |
c – b
c – d
|
|
вещественно и отрицательно. Число q
- это двойное отношение чисел a, b, c, d. Согласно
задаче 29.28, б) оно вещественно тогда и только тогда, когда данные
точки лежат на одной окружности. Остается доказать, что если данные точки лежат
на одной окружности, то q отрицательно тогда и только тогда, когда ломаная
abcd несамопересекающаяся. Последнее условие эквивалентно тому, что точки b
и d лежат на разных дугах, высекаемых точками a и c. Отобразим нашу
окружность при помощи инверсии на прямую. В решении задачи 29.27
показано, что двойное отношение сохраняется при инверсии. Поэтому если
a*, b*, c*, d* - комплексные числа, соответствующие образам наших
точек, то их двойное отношение равно q. Рассматривая всевозможные (с
точностью до порядка) способы расположения точек a*, b*, c*, d* на
прямой, легко убедиться, что q < 0 тогда и только тогда, когда на отрезке
aўcў лежит ровно одна из точек bў и dў.
г) Задачу б) можно следующим образом решить с помощью неравенства Птолемея:
|
A1A2 · A3A6 · A4A5 + A1A2 · A3A4 · A5A6 + |
|
|
+ A2A3 · A1A4 · A5A6 + A2A3 · A4A5 · A1A6 + A3A4 · A2A5 · A1A6 = |
|
|
= A1A2 · A3A6 · A4A5 + (A1A2 · A3A4 + A2A3 · A1A4) · A5A6 + |
|
|
+ (A2A3 · A4A5 + A3A4 · A2A5) · A1A6 і |
|
|
і A1A2 · A3A6 · A4A5 + A1A3 · A2A4 · A5A6 + A2A4 · A3A5 · A1A6 = |
|
|
= A1A2 · A3A6 · A4A5 + (A1A3 · A5A6 + A3A5 · A1A6) · A2A4 і |
|
|
і A1A2 · A3A6 · A4A5 + A1A5 · A3A6 · A2A4 = |
|
|
= (A1A2 · A4A5 + A1A5 · A2A4) · A3A6 і A1A4 · A2A5 · A3A6. |
|
Все использованные нестрогие неравенства обращаются в равенства тогда и только
тогда, когда четырехугольники A1A2A3A4, A2A3A4A5, A1A3A5A6 и
A1A2A4A5 вписанные. Легко видеть, что это эквивалентно тому, что
шестиугольник A1… A6 вписанный.
-
29.30.
-
Докажем сначала, что если u, v, w, z - комплексные числа, причем
u + v + w + z = 0, то
|
|uw – vz|2 = |u + v|2|v + w|2. |
|
В самом деле,
|
|uw – vz| = |uw + v(u + v + w)| = |u + v| · |v + w|. |
|
Пусть комплексные числа u, v, w, z соответствуют векторам
,
,
,
. Тогда |u + v|2|v + w|2 = m2n2 и
|
|uw – vz|2 = (uw – vz)( |
-
u
|
|
-
w
|
– |
-
v
|
|
-
z
|
) = |uw|2 + |vz|2 – (uw |
-
v
|
|
-
z
|
– |
-
u
|
|
-
w
|
vz). |
|
Так как |uw|2 = a2c2 и |vz|2 = b2d2, то остается доказать, что
|
uw |
-
v
|
|
-
z
|
– |
-
u
|
|
-
w
|
vz = 2abcdcos (A + C). |
|
Для этого достаточно проверить, что аргумент числа
равен
±(РA + РC). Остается заметить, что аргумент числа
(соответственно
) равен ±j, где j - угол между
векторами u и v (соответственно w и z).
-
29.31.
-
а) Расположим треугольник ABC на комплексной плоскости так, чтобы точка X
совпала с нулем. Пусть a, b, g - комплексные числа,
соответствующие вершинам треугольника. Требуемое неравенство следует из
тождества
|
|
b
a – g
|
· |
g
a – b
|
+ |
g
a – b
|
· |
a
b – g
|
+ |
a
g – b
|
· |
b
g – a
|
= 1. |
|
б) Описанные окружности треугольников AB1C1, A1BC1 и A1B1C
пересекаются в некоторой точке X (задача 2.81, а)). Пусть Ra, Rb, Rc
- радиусы этих окружностей, R - радиус описанной окружности треугольника
ABC. Тогда
|
a2b1c1 + b2a1c1 + c2a1b1 = 8Rsin Asin Bsin C(aRbRc + bRcRb + cRaRb) = |
|
|
= |
4S
R
|
(aRbRc + bRcRb + cRaRb). |
|
Ясно, что 2Ra і XA, 2Rb і XB, 2Rc і XC. Поэтому
|
|
4S
R
|
(aRbRc + bRcRb + cRaRb) і |
|
|
і |
abcS
R
|
|
ж
и
|
XB
b
|
· |
XC
c
|
+ |
XC
c
|
· |
XA
a
|
+ |
XA
a
|
· |
XB
b
|
ц
ш
|
і |
abcS
R
|
= 4S2. |
|
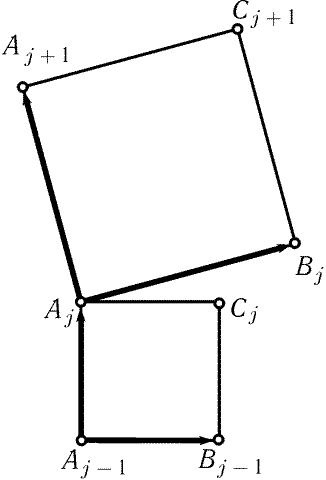
Рис. 29.6
29.32.
Установим соответствие между точками плоскости и комплексными
числами так, чтобы точка O совпала с нулем. Тогда
Bj – Aj = – i(Aj + 1 – Aj) и Cj – Aj = – i(Aj – Aj – 1) (см.
рис. 29.6; мы считаем, что A0 = An и An + 1 = A1). Вычитая
второе равенство из первого, получаем
Bj – Cj = – i(Aj – 1 + Aj + 1 – 2Aj).
Но согласно задаче 29.10 Aj – 1 + Aj + 1 = 2cos (2p/n)Aj. Значит,
| Bj – Cj = 2i |
ж
и
|
1 – cos (2p/n) |
ц
ш
|
Aj
|
.
29.33.
Пусть A1… An - исходный n-угольник, причем его вершины занумерованы
против часовой стрелки; Bj - центр правильного n-угольника, построенного
внешним образом на стороне AjAj + 1. Будем считать, что точки плоскости
отождествлены с комплексными числами. Обозначим через w комплексное число
cos (2p/n) + isin (2p/n). Умножение на w (соответственно на
)
является поворотом вокруг нуля на угол 2p/n против часовой стрелки
(соответственно по часовой стрелке). Точка Aj при повороте вокруг Bj – 1
на угол 2p/n против часовой стрелки переходит в точку Aj – 1, а при
повороте вокруг Bj по часовой стрелке - в точку Aj + 1. Поэтому имеют
место равенства
|
Aj – 1 – Bj – 1 = w(Aj – Bj – 1), Aj + 1 – Bj = |
-
w
|
(Aj – Bj) |
|
для всех j = 1,…,n (здесь и далее мы будем считать, что A0 = An и
An + 1 = A1). Следовательно,
|
Bj – 1(w – 1) = wAj – Aj – 1, Bj( |
-
w
|
– 1) = |
-
w
|
Aj – Aj + 1. |
|
Сложим эти равенства. Учитывая, что
, получим
|
(Bj – wBj – 1)( |
-
w
|
– 1) = (w + |
-
w
|
)Aj – Aj – 1 – Aj + 1 |
| (1) |
для всех j = 1,…,n.
Многоугольник B1B1… Bn является правильным тогда и только тогда, когда
соответствие между точками плоскости и комплексными числами можно установить
так, что Bj = wBj – 1 для всех j = 1,…,n, т. е. при всех j левая
часть (1) равна нулю.
С другой стороны, согласно задаче 29.10 многоугольник A1A2… An
аффинно правильный тогда и только тогда, когда соответствие между точками
плоскости и комплексными числами можно установить так, что
cos (2p/n)Aj = Aj – 1 + Aj + 1 для всех j = 1,…,n. Поскольку
, последнее условие эквивалентно тому, что правая
часть (1) равна нулю.
-
29.34.
-
Согласно задаче 29.20
|
|
Im
| (a – z)(a – w)( |
-
a
|
– |
-
b
|
)( |
-
a
|
– |
-
c
|
) = 0. |
|
Обозначим
| ( |
-
a
|
– |
-
b
|
)( |
-
a
|
– |
-
c
|
)
|
,
| ( |
-
b
|
– |
-
a
|
)( |
-
b
|
– |
-
c
|
)
|
и
| ( |
-
c
|
– |
-
a
|
)( |
-
c
|
– |
-
b
|
)
|
через A, B и C соответственно. Тогда
|
|
Im
| a2A – |
Im
| aA(z + w) + |
Im
| Azw = 0. |
| (1) |
Заметим, что a(b + c)A - вещественное число. Действительно,
|
a(b + c)A = 2В |
ж
и
|
|
-
a
|
(b + c) |
ц
ш
|
– |a(b + c)|2 |
|
(чтобы проверить это равенство, нужно воспользоваться тем, что
, и тем, что
| a |
-
a
|
= b |
-
b
|
= c |
-
c
|
= 1
|
,
поскольку точки a, b, c лежат на единичной окружности). Таким образом,
|
|
Im
| a2A = Б |
ж
и
|
(a + b + c)aA |
ц
ш
|
– Б |
ж
и
|
a(b + c)A |
ц
ш
|
= Б |
ж
и
|
aA(a + b + c) |
ц
ш
|
. |
|
Далее,
|
abc · aA = ab( |
-
a
|
– |
-
b
|
) · ac( |
-
a
|
– |
-
c
|
) = (a – b)(a – c) = |
-
A
|
. |
|
Следовательно,
|
|
Im
| Azw = – Б |
Azw
|
= – |
Im
| aA · abc · |
-
z
|
|
-
w
|
. |
|
Подставляя эти равенства в (1), получаем
|
|
Im
| aA[a + b + c – (z + w) – abc · |
-
z
|
|
-
w
|
] = |
Im
| aAp = 0 |
|
(через p обозначено выражение в квадратных скобках).
Аналогично доказывается, что
. Таким образом, либо p = 0 и
тогда утверждение задачи доказано, либо числа aA, bB и cC пропорциональны
с вещественным коэффициентом пропорциональности. Но второй случай невозможен,
так как иначе число
Рис. 29.7
было бы вещественным, т. е. РbOa = Рacc1 = pn (углы
ориентированные: рис. 29.7). Однако Рacc1 = p – Рc и
РbOa = 2Рc по теореме о вписанном угле, поэтому
Рc = p(n – 1), чего не может быть.
29.35.
Расположим данный правильный треугольник на комплексной плоскости так, чтобы
центр его описанной окружности оказался в нуле и радиус описанной окружности
был равен 1. Пусть z и w - комплексные числа, соответствующие точкам
Z и W. Согласно задаче 29.34
, т. е.
. Ясно, что
и
.
Следовательно,
|
|
1
2
|
(z* + w*) = |
1
2
|
|
ж
з
и
|
1
|
+ |
1
|
ц
ч
ш
|
= |
1
2
|
|
|
= – |
1
2
|
|
z
|
|
w
|
. |
|
модуль этого числа равен
.
-
29.36.
-
Расположим данный треугольник так, чтобы центр описанной окружности оказался в
нуле, а точка A - в единице. Пусть z и w - комплексные числа,
соответствующие точкам Z и W. Повороты плоскости вокруг нуля на указанные
углы соответствуют умножению на комплексные числа
,
и
. Но согласно задаче 29.34
,
значит, произведение этих трех комплексных чисел равно 1.
-
29.37.
-
Барицентрические координаты точки не изменяются при аффинном преобразовании,
поэтому эллипсы Штейнера задаются такими же уравнениями, как вписанная и
описанная окружности. Поэтому описанный эллипс Штейнера в барицентрических
координатах (a : b : g) задается уравнением
bg + ag + ab = 0 (задача 14.39),
а вписанный - уравнением
|
2bg + 2ag + 2ab = a2 + b2 + g2 |
|
(задача 14.45, б)).
-
29.38.
-
Описанный эллипс Штейнера задается уравнением
bg + ag + ab = 0
(задача 29.37), а описанная окружность - уравнением
a2bg + b2ag + c2ab = 0, где a, b,
c - длины сторон (задача 14.37). Из первого уравнения
получаем g = – ab/(a + b). Подставив это
выражение во второе уравнение, получим
a : b = (b2 – c2) : (c2 – a2). Таким образом, точка
Штейнера имеет барицентрические координаты
|
(b2 – c2 : c2 – a2 : a2 – b2). |
|
Замечание.
На с. 392
дано другое определение точки Штейнера.
Задача 14.50 показывает, что эти определения эквивалентны.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:47.

 Глава 29. § -1 |
Глава 29. § -1 | 

 Глава 29. § -1 |
Глава 29. § -1 | 


