| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
§ 3. Касающиеся окружности
-
3.15.
-
Две окружности касаются в точке A. К ним
проведена общая (внешняя) касательная, касающаяся окружностей
в точках C и D. Докажите, что РCAD = 90°.
-
3.16.
-
Две окружности S1 и S2 с центрами O1 и O2
касаются в точке A. Через точку A проведена прямая,
пересекающая S1 в точке A1 и S2 в точке A2. Докажите,
что O1A1||O2A2.
-
3.17.
-
Три окружности S1,S2 и S3 попарно касаются друг
друга в трех различных точках. Докажите, что прямые,
соединяющие точку касания окружностей S1 и S2 с двумя
другими точками касания, пересекают окружность S3 в точках,
являющихся концами ее диаметра.
-
3.18.
-
Две касающиеся окружности с центрами O1
и O2 касаются внутренним образом окружности радиуса R
с центром O. Найдите периметр треугольника OO1O2.
-
3.19.
-
Окружности S1 и S2 касаются окружности S
внутренним образом в точках A и B, причем одна из точек
пересечения окружностей S1 и S2 лежит на отрезке AB.
Докажите, что сумма радиусов окружностей S1 и S2 равна
радиусу окружности S.
-
3.20.
-
Радиусы окружностей S1 и S2, касающихся в
точке A, равны R и r (R > r). Найдите длину касательной,
проведенной к окружности S2 из точки B окружности S1, если
известно, что AB = a. (Разберите случаи внутреннего и внешнего касания.)
-
3.21.
-
На отрезке AB взята точка C. Прямая, проходящая
через точку C, пересекает окружности с диаметрами AC
и BC в точках K и L, а окружность с диаметром AB- в
точках M и N. Докажите, что KM = LN.
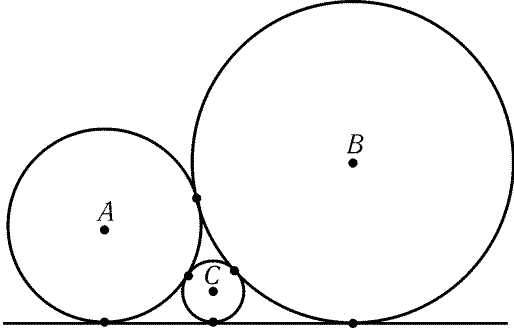
Рис. 3.2
3.22. Даны четыре окружности S1,S2,S3 и S4, причем
окружности Si и Si + 1 касаются внешним образом для i = 1,2,3,4(S5 = S1). Докажите, что точки касания образуют вписанный
четырехугольник.
3.23. а) Три окружности с центрами A,B,C, касающиеся
друг друга и прямой l, расположены так, как показано на
рис. 3.2. Пусть a,b и c- радиусы окружностей с центрами A,B,C.
Докажите, что 1/Цc = 1/Цa + 1/Цb.
б) Четыре окружности попарно касаются внешним образом
(в шести различных точках). Пусть a,b,c,d — их
радиусы, a
= 1/a, b
= 1/b, g
= 1/c и d
= 1/d. Докажите, что
2(a2 + b2 + g2 + d2) = (a + b + g + d)2.

 Глава 3. § 2 |
Глава 3. § 2 | 

 Глава 3. § 2 |
Глава 3. § 2 | 

 Глава 3. § 2 |
Глава 3. § 2 | 
