
 Глава 4 |
Глава 4 | 
| Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
 |
||
 Глава 4 | Глава 4 | |
Оглавление | | Глава 4. § 2  |
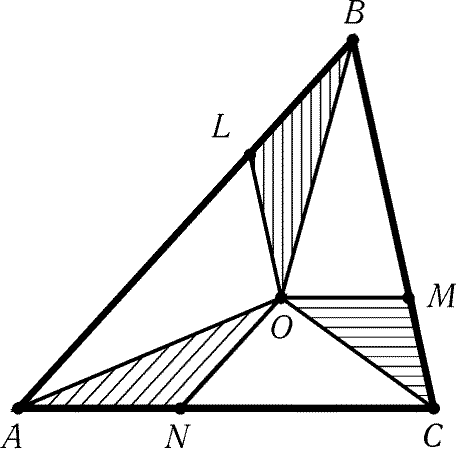
Рис. 4.1
4.3. Внутри данного треугольника ABC найдите такую точку O, что площади треугольников BOL,COM и AON равны (точки L,M и N лежат на сторонах AB,BC и CA, причем OL||BC, OM||AC и ON||AB; рис. 4.1).
4.4. На продолжениях сторон треугольника ABC взяты
точки A1, B1 и C1 так,
что
|
® AB1 | = 2 |
® AB |
|
® BC1 | = 2 |
® BC |
|
® CA1 | = 2 |
® AC |
4.5. На продолжениях сторон DA, AB, BC, CD выпуклого
четырехугольника ABCD взяты точки A1,B1,C1,D1 так,
что
|
® DA1 | = 2 |
® DA |
|
® AB1 | = 2 |
® AB |
|
® BC1 | = 2 |
® BC |
|
® CD1 | = 2 |
® CD |
4.6*. Шестиугольник ABCDEF вписан в окружность. Диагонали AD,BE и CF являются диаметрами этой окружности. Докажите, что площадь шестиугольника ABCDEF равна удвоенной площади треугольника ACE.
 Глава 4 | Глава 4 | |
Оглавление | | Глава 4. § 2  |
 |
| Copyright © 2002 МЦНМО |
Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru. |
|