
 Глава 4. § 1 |
Глава 4. § 1 | 
| Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
 |
||
 Глава 4. § 1 | Глава 4. § 1 | |
Оглавление | | Глава 4. § 3  |
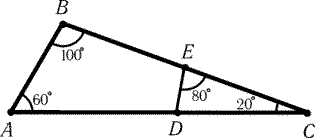
Рис. 4.2
4.11*. В треугольнике ABC точка E- середина стороны BC, точка D лежит на стороне AC, AC = 1, РBAC = 60°, РABC = 100°, РACB = 20° и РDEC = 80° (рис. 4.2). Чему равна сумма площади треугольника ABC и удвоенной площади треугольника CDE?
4.12*. В треугольник Ta = DA1A2A3 вписан треугольник Tb = DB1B2B3, а в треугольник Tb вписан треугольник Tc = DC1C2C3, причем стороны треугольников Ta и Tc параллельны. Выразите площадь треугольника Tb через площади треугольников Ta и Tc.
4.13*. На сторонах треугольника ABC взяты точки A1,B1 и C1, делящие его стороны в отношениях BA1 : A1C = p,CB1 : B1A = q и AC1 : C1B = r. Точки пересечения отрезков AA1,BB1 и CC1 расположены так, как показано на рис. 4.3. Найдите отношение площадей треугольников PQR и ABC.
 Глава 4. § 1 | Глава 4. § 1 | |
Оглавление | | Глава 4. § 3  |
 |
| Copyright © 2002 МЦНМО |
Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru. |
|