| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
§ 4. Площади частей, на которые разбит
четырехугольник
-
4.18.
-
Пусть K,L,M и N- середины сторон AB,BC,CD
и DA выпуклого четырехугольника ABCD; отрезки KM и LN
пересекаются в точке O. Докажите, что
|
SAKON + SCLOM = SBKOL + SDNOM. |
|
-
4.19.
-
Точки K,L,M и N лежат на сторонах AB,BC,CD
и DA параллелограмма ABCD, причем отрезки KM
и LN параллельны сторонам параллелограмма. Эти отрезки
пересекаются в точке O. Докажите, что площади параллелограммов KBLO
и MDNO равны тогда и только тогда, когда точка O лежит на
диагонали AC.
-
4.20.
-
На сторонах AB и CD четырехугольника ABCD
взяты точки M и N так, что AM : MB = CN : ND. Отрезки AN
и DM пересекаются в точке K, а отрезки BN и CM- в
точке L. Докажите, что SKMLN = SADK + SBCL.
-
4.21.
-
На стороне AB четырехугольника ABCD взяты точки A1
и B1, а на стороне CD- точки C1 и D1,
причем AA1 = BB1 = pAB и CC1 = DD1 = pCD, где p < 0,5. Докажите,
что SA1B1C1D1/SABCD = 1 – 2p.
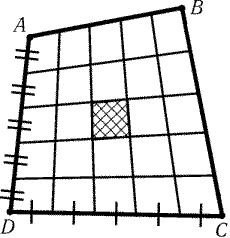
Рис. 4.4
4.22*. Каждая из сторон выпуклого четырехугольника разделена
на пять равных частей и соответствующие точки противоположных сторон
соединены (рис. 4.4). Докажите, что площадь среднего (заштрихованного)
четырехугольника в 25 раз меньше площади исходного.
4.23*. На каждой стороне параллелограмма взято по точке.
Площадь четырехугольника с вершинами в этих точках равна половине
площади параллелограмма. Докажите, что хотя бы одна из диагоналей
четырехугольника параллельна стороне параллелограмма.
-
4.24*.
-
Точки K и M- середины сторон AB и CD
выпуклого четырехугольника ABCD, точки L и N расположены на
сторонах BC и AD так, что KLMN- прямоугольник.
Докажите, что площадь четырехугольника ABCD вдвое
больше площади прямоугольника KLMN.
-
4.25*.
-
Квадрат разделен на четыре части двумя
перпендикулярными прямыми, точка пересечения которых лежит
внутри его. Докажите, что если площади трех из этих частей
равны, то равны и площади всех четырех частей.

 Глава 4. § 3 |
Глава 4. § 3 | 

 Глава 4. § 3 |
Глава 4. § 3 | 

 Глава 4. § 3 |
Глава 4. § 3 | 
