| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
§ 5. Разные задачи
-
4.26.
-
Даны параллелограмм ABCD и некоторая точка M.
Докажите, что SACM = |SABM±SADM|.
-
4.27.
-
На сторонах AB и BC треугольника ABC внешним
образом построены параллелограммы; P- точка пересечения
продолжений их сторон, параллельных AB и BC. На стороне AC
построен параллелограмм, вторая сторона которого равна
и параллельна BP. Докажите, что его площадь равна сумме
площадей первых двух параллелограммов.
-
4.28*.
-
Точка O, лежащая внутри правильного шестиугольника,
соединена с вершинами. Возникшие при этом шесть
треугольников раскрашены попеременно в красный и синий
цвет. Докажите, что сумма площадей красных треугольников
равна сумме площадей синих.
-
4.29*.
-
Продолжения сторон AD и BC выпуклого
четырехугольника ABCD пересекаются в точке O; M
и N- середины сторон AB и CD, P и Q- середины
диагоналей AC и BD. Докажите, что:
а) SPMQN = |SABD – SACD|/2;
б) SOPQ = SABCD/4.
-
4.30*.
-
На сторонах AB и CD выпуклого четырехугольника ABCD
взяты точки E и F. Пусть K,L,M и N- середины
отрезков DE,BF,CE и AF. Докажите, что четырехугольник KLMN
выпуклый и его площадь не зависит от выбора точек E и F.
-
4.31*.
-
Середины диагоналей AC,BD,CE,… выпуклого
шестиугольника ABCDEF образуют выпуклый шестиугольник.
Докажите, что его площадь в четыре раза меньше площади
исходного шестиугольника.
-
4.32*.
-
Диаметр PQ и перпендикулярная ему хорда RS
пересекаются в точке A. Точка C лежит на окружности,
а точка B- внутри окружности, причем BC||PQ и BC = RA.
Из точек A и B опущены перпендикуляры AK и BL на
прямую CQ. Докажите, что SACK = SBCL.
-
4.33*.
-
Через точку O, лежащую внутри треугольника ABC,
проведены отрезки, параллельные сторонам. Отрезки AA1,BB1
и CC1
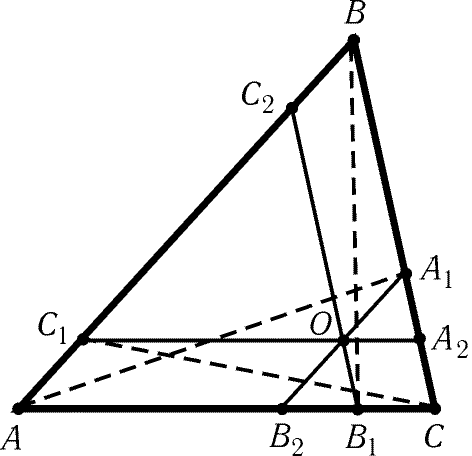
Рис. 4.5
разбивают треугольник ABC на четыре треугольника и три
четырехугольника (рис. 4.5). Докажите, что сумма площадей треугольников,
прилегающих к вершинам A,B и C, равна площади четвертого
треугольника.
4.34*. На биссектрисе угла A треугольника ABC взята
точка A1 так, что AA1 = p – a = (b + c – a)/2, и через точку A1
проведена прямая la, перпендикулярная биссектрисе. Если аналогично
провести прямые lb и lc, то треугольник ABC разобьется на
части, среди которых четыре треугольника. Докажите, что площадь одного
из этих треугольников равна сумме площадей трех других.
См. также задачи 3.38-3.41, 13.52-13.56, 16.5, 24.5.

 Глава 4. § 4 |
Глава 4. § 4 | 

 Глава 4. § 4 |
Глава 4. § 4 | 

 Глава 4. § 4 |
Глава 4. § 4 | 
