Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!)	МЦНМО, 2002


Глава 4. § 8 \|	Оглавление \|	Глава 4. Задачи для самостоятельного решения

§ 9. Перегруппировка площадей

4.59.: Докажите, что площадь правильного восьмиугольника равна произведению длин наибольшей и наименьшей его диагоналей.

4.60.

Из середины каждой стороны остроугольного треугольника опущены перпендикуляры на две другие стороны. Докажите, что площадь ограниченного ими шестиугольника равна половине площади исходного треугольника.

Рис. 4.6

4.61^*.: Стороны AB и CD параллелограмма ABCD площади 1 разбиты на n равных частей, AD и BC- на m равных частей.

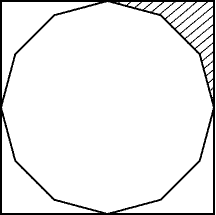
Рис. 4.7

а) Точки деления соединены так, как показано на рис. 4.6, а .

б) Точки деления соединены так, как показано на рис. 4.6, б .

Чему равны площади образовавшихся при этом маленьких параллелограммов?

4.62^*. а) Четыре вершины правильного двенадцатиугольника расположены в серединах сторон квадрата (рис. 4.7). Докажите, что площадь заштрихованной части в 12 раз меньше площади двенадцатиугольника.

б) Докажите, что площадь двенадцатиугольника, вписанного в окружность радиуса 1, равна 3.

Глава 4. § 8 \|	Оглавление \|	Глава 4. Задачи для самостоятельного решения

Внимание! Данное издание содержит опечатки!
Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора.
Заказ книги: biblio@mccme.ru.