| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
4.1.
-
Треугольники, прилегающие к одной стороне, имеют равные
основания и общую высоту, поэтому они равновелики. Пусть M-
точка пересечения медиан треугольника ABC. Прямая BM
разрезает каждый из треугольников ABC и AMC на два равновеликих
треугольника, поэтому SABM = SBCM. Аналогично SBCM = SCAM.
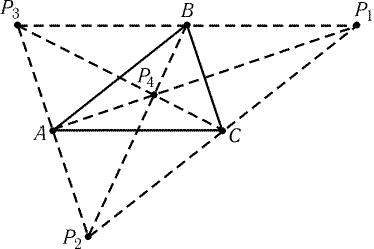
Рис. 4.8
4.2. Из равенства площадей треугольников ABP и BCP следует,
что расстояния от точек A и C до прямой BP равны. Поэтому
прямая BP либо проходит через середину отрезка AC, либо
параллельна ему. Искомые точки изображены на рис. 4.8.
4.3. Обозначим точку пересечения прямой LO со стороной AC
через L1. Так как SLOB = SMOC и DMOC = D
L1OC, то SLOB = SL1OC. Высоты треугольников LOB и L1OC
равны, поэтому LO = L1O, т. е. точка O лежит на медиане,
проведенной из вершины A. Аналогично доказывается, что
точка O лежит на медианах, проведенных из вершин B и C,
т. е. O- точка пересечения медиан треугольника. Проведенные
рассуждения показывают также, что точка пересечения медиан
треугольника обладает требуемым свойством.
-
4.4.
-
Так как SA1BB1 = SA1AB = SABC,
то SAA1B1 = 2S. Аналогично SBB1C1 = SCC1A1 = 2S.
Поэтому SABC = 7S.
-
4.5.
-
Поскольку AB = BB1, то SBB1C = SBAC. А так
как BC = CC1, то SB1C1C = SBB1C = SBAC
и SBB1C1 = 2SBAC. Аналогично SDD1A1 = 2SACD, поэтому
SBB1C1 + SDD1A1 = 2SABC + 2SACD = 2SABCD.
Аналогично SAA1B1 + SCC1D1 = 2SABCD,
поэтому SA1B1C1D1 = SABCD + SAA1B1 + SBB1C1 + SCC1D1 + SDD1A1 = 5SABCD.
-
4.6.
-
Пусть O- центр описанной окружности. Так как AD,BE
и CF- диаметры, то SABO = SDEO = SAEO,
SBCO = SEFO = SCEO, SCDO = SAFO = SACO.
Ясно также, что SABCDEF = 2(SABO + SBCO + SCDO)
и SACE = SAEO + SCEO + SACO. Следовательно,
SABCDEF = 2SACE.
-
4.7.
-
Пусть E и F- середины диагоналей AC и BD. Так
как SAOB = SAOD, точка O лежит на прямой AF. Аналогично
точка O лежит на прямой CF. Предположим, что точка пересечения
диагоналей не является серединой ни одной из них. Тогда прямые AF
и CF имеют единственную общую точку F, поэтому O = F.
Аналогично доказывается, что O = E. Получено противоречие.
-
4.8.
-
Пусть диагональ AC трапеции ABCD с основанием AD
равна 5. Достроим треугольник ACB до параллелограмма ACBE.
Площадь трапеции ABCD равна площади прямоугольного
треугольника DBE. Пусть BH- высота треугольника DBE.
Тогда EH2 = BE2 – BH2 = 52 – 42 = 32 и ED = BE2/EH = 25/3.
Поэтому SDBE = ED · BH/2 = 50/3.
-
4.9.
-
Так как SABE = SABC, то EC||AB. Остальные
диагонали тоже параллельны соответствующим сторонам.
Пусть P- точка пересечения BD и EC. Если SBPC = x, то
SABCDE = SABE + SEPB + SEDC + SBPC = 3 + x
(SEPB = SABE = 1, так как ABPE- параллелограмм). Так как
SBPC : SDPC = BP : DP = SEPB : SEPD,
то x : (1 – x) = 1 : x, а значит, x = (Ц5 – 1)/2
и SABCDE = (Ц5 + 5)/2.
-
4.10.
-
Центры всех трех прямоугольников совпадают (см.
задачу 1.7), поэтому два меньших прямоугольника имеют общую
диагональ KL. Пусть M и N- вершины этих прямоугольников,
лежащие на стороне BC. Точки M и N лежат на окружности с
диаметром KL. Пусть O- центр этой окружности. O1-
проекция точки O на BC. Тогда BO1 = CO1 и MO1 = NO1, а значит,
BM = NC. Чтобы доказать, что SKLM + SKLN = SKBCL, достаточно
проверить, что (SKBM + SLCM) + (SKBN + SLCN) = SKBCL = BC(KB + CL)/2 = BC · AB/2. Остается заметить, что KB · BM + KB · BN = KB · BC, LC · CM + LC · CN = LC · BC
и KB · BC + LC · BC = AB · BC.
-
4.11.
-
Опустим из точки C перпендикуляр l на прямую AB.
Пусть точки Aў,Bў и Eў симметричны точкам A,B и E относительно
прямой l. Тогда треугольник AAўC равносторонний, причем РACB = РBCBў = РBўCAў = 20°. Треугольники EEўC и DEC
равнобедренные с углом при вершине 20°, причем боковая
сторона EC у них общая. Следовательно,
SABC + 2SEDC = SABC + 2SEEўC. Так как E середина BC,
то 2SEEўC = SBEўC = SBBўC/2.
Поэтому SABC + 2SEDC = SAAўC/2 = Ц3/8.
-
4.12.
-
Пусть площади треугольников Ta,Tb и Tc
равны a,b и c. Треугольники Ta и Tc гомотетичны, поэтому
прямые, соединяющие их соответственные вершины, пересекаются в одной
точке O. Коэффициент k подобия этих треугольников
равен
. Ясно, что SA1B3O :
SC1B3O = A1O : C1O = k. Записывая аналогичные равенства и
складывая их, получаем a : b = k, а значит,
.
-
4.13.
-
Воспользовавшись результатом задачи 1.3, легко проверить,
что
|
|
BQ
BB1
|
= |
p + pq
1 + p + pq
|
, |
B1R
BB1
|
= |
qr
1 + q + qr
|
, |
CR
CC1
|
= |
q + qr
1 + q + qr
|
, |
CP
CC1
|
= |
pr
1 + r + pr
|
. |
|
Ясно также, что
|
|
SPQR
SRB1C
|
= |
QR
RB1
|
· |
PR
RC
|
и |
SRB1C
SABC
|
= |
B1C
AC
|
· |
B1R
BB1
|
. |
|
Поэтому
|
|
SPQR
SABC
|
= |
QR
BB1
|
· |
PR
RC
|
· |
B1C
AC
|
= |
QR
BB1
|
· |
PR
CC1
|
· |
CC1
CR
|
· |
B1C
AC
|
. |
|
Учитывая, что
|
|
QR
BB1
|
= 1 – |
p + pq
1 + p + pq
|
– |
qr
1 + q + rq
|
= |
1
1 + p + pq
|
– |
rq
1 + q + rq
|
= |
(1 + q)(1 – pqr)
(1 + p + pq)(1 + q + qr)
|
|
|
и
|
|
PR
CC1
|
= |
(1 + r)(1 – pqr)
(1 + q + qr)(1 + r + pr)
|
, |
|
получаем
|
|
SPQR
SABC
|
= |
(1 – pqr)2
(1 + p + pq)(1 + q + qr)(1 + r + pr)
|
. |
|
-
4.14.
-
Если SAOB = SCOD, то AO · BO = CO · DO.
Поэтому DAOD ~ DCOB и AD||BC. Эти рассуждения
обратимы.
-
4.15.
-
а) Так как SADP : SABP = DP :
BP = SCDP : SBCP, то SADP = SABP · SCDP/SBCP.
б) Согласно задаче a) SADP · SCBP = SABP · SCDP.
Поэтому
|
SABP · SCBP · SCDP · SADP = (SADP · SCBP)2. |
|
-
4.16.
-
После сокращения на sin 2j/4, где j- угол
между диагоналями, данное равенство площадей перепишется в виде
(AP · BP)2 + (CP · DP)2 = (BP · CP)2 + (AP · DP)2,
т. е. (AP2 – CP2)(BP2 – DP2) = 0.
-
4.17.
-
Предположим, что четырехугольник ABCD не параллелограмм;
например, прямые AB и CD пересекаются. Согласно задаче 7.2
множеством точек P, лежащих внутри четырехугольника ABCD, для
которых SABP + SCDP = SBCP + SADP = SABCD/2, является отрезок.
Следовательно, точки P1,P2 и P3 лежат на одной прямой. Получено
противоречие.
-
4.18.
-
Ясно, что SAKON = SAKO + SANO = (SAOB + SAOD)/2.
Аналогично SCLOM = (SBCO + SCOD)/2.
Поэтому SAKON + SCLOM = SABCD/2.
-
4.19.
-
Если площади параллелограммов KBLO и MDNO равны,
то OK · OL = OM · ON. Учитывая, что ON = KA и OM = LC,
получаем KO : KA = LC : LO. Следовательно, D
KOA ~ DLCO, а значит, точка O лежит на диагонали AC.
Эти рассуждения обратимы.
-
4.20.
-
Пусть h1,h и h2- расстояния от точек A,M
и B до прямой CD. Согласно задаче 1.1, б) h = ph2 + (1 – p)h1,
где p = AM/AB. Поэтому SDMC = h · DC/2 = (h2p · DC + h1(1 – p) · DC)/2 = SBCN + SADN. Вычитая из обеих частей этого
равенства SDKN + SCLN, получаем требуемое.
-
4.21.
-
Согласно задаче 4.20
SABD1 + SCDB1 = SABCD.
Поэтому
SA1B1C1D1 = SA1B1D1 + SC1D1B1 = (1 – 2p)SABD1 + (1 – 2p)SCDB1 = (1 – 2p)SABCD.
-
4.22.
-
Согласно задаче 4.21 площадь среднего из
четырехугольников, заданных отрезками, соединяющими точки сторон AB
и CD, в пять раз меньше площади исходного четырехугольника. А так как
каждый из рассматриваемых отрезков делится отрезками, соединяющими
соответствующие точки другой пары противоположных сторон, на пять
равных частей (см. задачу 1.16), то, воспользовавшись еще раз
результатом задачи 4.21, получим требуемое.
-
4.23.
-
На сторонах AB,BC,CD и AD взяты точки K,L,M
и N соответственно. Предположим, что диагональ KM не
параллельна стороне AD. Фиксируем точки K,M,N и будем
двигать точку L по стороне BC. При этом площадь треугольника KLM
изменяется строго монотонно. Кроме того, если LN||AB, то
выполняется равенство SAKN + SBKL + SCLM + SDMN = SABCD/2,
т. е. SKLMN = SABCD/2.
-
4.24.
-
Пусть L1 и N1- середины сторон BC и AD
соответственно. Тогда KL1MN1- параллелограмм и его площадь
равна половине площади четырехугольника ABCD (см. задачу 1.38, а)).
Поэтому достаточно доказать, что площади параллелограммов KLMN
и KL1MN1 равны. Если эти параллелограммы совпадают, то доказывать
больше ничего не нужно, а если они не совпадают, то, так как середина
отрезка KM является их центром симметрии, LL1||NN1 и BC||
AD. В этом случае средняя линия KM трапеции ABCD параллельна
основаниям BC и AD, и поэтому высоты треугольников KLM и KL1M,
опущенные на сторону KM, равны, т. е. равны площади
параллелограммов KLMN и KL1MN1.
-
4.25.
-
Пусть данные прямые l1 и l2 делят квадрат на четыре
части, площади которых равны S1,S2,S3 и S4, причем для первой
прямой площади частей, на которые она делит квадрат, равны S1 + S2
и S3 + S4 а для второй они равны S2 + S3 и S1 + S4. Так
как по условию S1 = S2 = S3, то S1 + S2 = S2 + S3. Это означает, что
образ прямой l1 при повороте относительно центра квадрата
на + 90° или – 90° не просто параллелен прямой l2, а
совпадает с ней.
Остается доказать, что прямая l1 (а значит, и прямая l2)
проходит через центр квадрата. Предположим, что это не верно.
Рассмотрим образы прямых l1 и l2 при поворотах на + 90°
и обозначим площади частей, на которые они делят квадрат, так,
как показано на рис. 4.9 (на этом рисунке изображены оба различных
варианта расположения прямых). Прямые l1 и l2 делят квадрат на
четыре части, площади которых равны a,a + b,a + 2b + c и a + b,
причем числа a,b и c ненулевые. Ясно, что три из указанных
четырех чисел не могут быть равны. Получено противоречие.
-
4.26.
-
Все три рассматриваемых треугольника имеют общее
основание AM. Пусть hb,hc и hd- расстояния от точек B,C
и D до прямой AM. Так как
,
то hc = |hb±hd|.
-
4.27.
-
Можно считать, что P- общая точка параллелограммов,
построенных на сторонах AB и BC, т. е. эти параллелограммы
имеют вид ABPQ и CBPR. Ясно, что SACRQ = SABPQ + SCBPR.
-
4.28.
-
Пусть сторона данного шестиугольника равна a.
Продолжения красных сторон шестиугольника образуют правильный
треугольник со стороной 3a, причем сумма площадей красных
треугольников равна половине произведения a на сумму расстояний от
точки O до стороны этого треугольника, поэтому она
равна
(см. задачу 4.46). Сумма площадей синих
треугольников вычисляется аналогично.
-
4.29.
-
а) Площадь параллелограмма PMQN равна BC · ADsin a/4, где a- угол между прямыми AD и BC. Высоты
треугольников ABD и ACD, опущенные из вершин B и C,
равны OBsin a и OCsin a,
поэтому |SABD – SACD| = |OB – OC| · ADsin a/2 = BC · ADsin a/2.
б) Пусть для определенности пересекаются лучи AD и BC.
Так как PN||AO и QN||CO, точка N лежит внутри
треугольника OPQ. Поэтому
| SOPQ = SPQN + SPON + SQON = |
SPMQN
2
|
+ |
SACD
4
|
+ |
SBCD
4
|
= |
(SABD – SACD + SACD + SBCD)
4
|
= |
SABCD
4
|
|
.
-
4.30.
-
Отрезки KM и LN являются средними линиями
треугольников CED и AFB, поэтому они имеют общую точку- середину
отрезка EF. Кроме того, KM = CD/2, LN = AB/2 и угол между
прямыми KM и LN равен углу a между прямыми AB и CD.
Поэтому площадь четырехугольника KLMN равна AB · CDsin a/8.
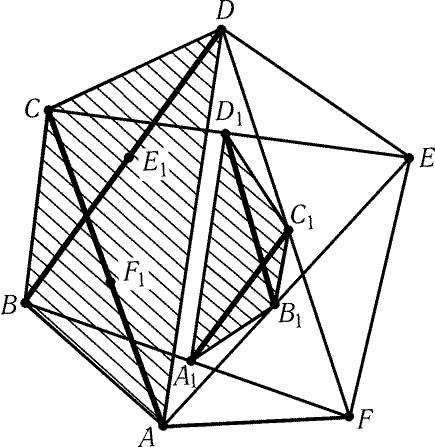
Рис. 4.10
4.31. Обозначим середины диагоналей шестиугольника ABCDEF
так, как показано на рис. 4.10. Докажем, что площадь
четырехугольника A1B1C1D1 в четыре раза меньше площади
четырехугольника ABCD. Воспользуемся для этого тем, что площадь
четырехугольника равна половине произведения длин диагоналей на синус
угла между ними. Так как A1C1 и B1D1- средние линии
треугольников BDF и ACE, получаем требуемое. Аналогично
доказывается, что площадь четырехугольника D1E1F1A1 в четыре раза
меньше площади четырехугольника DEFA.
4.32. Пусть a
= РPQC. Тогда
2SACK = CK · AK = (APcos a) · (AQsin a) =
= AR2sin acos a = BC2sin acos a
= BL · CL =
= 2SBCL.
4.33. Пусть Sa,Sb и Sc- площади треугольников,
прилегающих к вершинам A,B и C; S- площадь четвертого
рассматриваемого треугольника. Ясно, что
SACC1 + SBAA1 + SCBB1 = SABC – S + Sa + Sb + Sc.
Кроме того,
SABC = SAOC + SAOB + SBOC = SACC1 + SBAA1 + SCBB1.
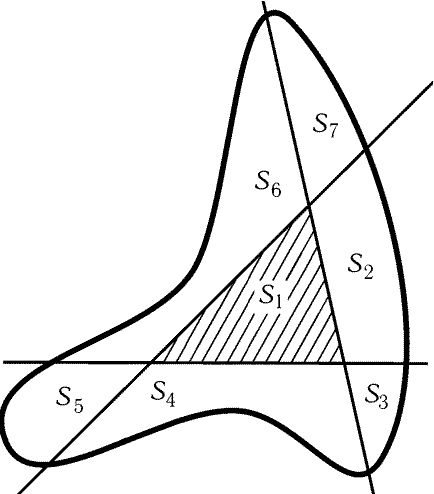
Рис. 4.11
4.34. Пусть O- центр вписанной окружности
треугольника ABC, B1- точка касания вписанной окружности со
стороной AC. Вырежем из треугольника ABC треугольник AOB1 и
отразим его симметрично относительно биссектрисы угла OAB1. При этом
прямая OB1 перейдет в прямую la. Проделаем такую операцию для
остальных треугольников. Общие части полученных при этом
треугольников являются тремя треугольниками рассматриваемого разбиения,
а непокрытая часть треугольника ABC- четвертым треугольником.
Ясно также, что площадь непокрытой части равна сумме площадей частей,
покрытых дважды.
4.35. Пусть для определенности лучи AD и BC пересекаются
в точке O. Тогда SCDO : SMNO = c2 : x2, где x = MN,
и SABO : SMNO = ab : x2, так как OA :
ON = a : x и OB : OM = b : x. Следовательно,
x2 – c2 = ab – x2, т. е. 2x2 = ab + c2.
4.36. Обозначим площади частей фигуры, на которые ее делят
прямые, так, как показано на рис. 4.11. Площадь всей фигуры
обозначим через S. Так как S3 + (S2 + S7) = S/2 = S1 + S6 + (S2 + S7),
то S3 = S1 + S6. Складывая это равенство с
равенством S/2 = S1 + S2 + S3 + S4, получаем S/2 = 2S1 + S2 + S4 + S6 і 2S1, т. е. S1 Ј S/4.
-
4.37.
-
Обозначим проекцию прямой l через B, крайние точки
проекции многоугольника- через A и C. Пусть C1- точка
многоугольника, проецирующаяся в точку C; прямая l пересекает
многоугольник в точках K и L, а K1 и L1- точки
прямых C1K и C1L, проецирующиеся в точку A (рис. 4.12).
Одна из частей, на которые прямая l делит многоугольник,
содержится в трапеции K1KLL1 другая часть содержит
треугольник C1KL. Поэтому SK1KLL1 і SC1KL,
т. е. AB · (KL + K1L1) і BC · KL. Так
как K1L1 = KL · (AB + BC)/BC, то AB · (2 + AB/BC) і BC. Решая
это квадратное неравенство, получаем BC/AB Ј 1 + Ц2.
Аналогично AB/BC Ј 1 + Ц2 (нужно провести те же рассуждения,
поменяв местами A и C).
-
4.38.
-
Обозначим площадь многоугольники через S.
Пусть l- произвольная прямая. Введем систему координат, для
которой прямая l является осью Ox. Пусть S(a)- площадь той
части многоугольника, которая лежит ниже прямой y = a. При изменении a
от – Ґ до + Ґ S(a) непрерывно меняется от 0 до S,
поэтому S(a) = S/2 для некоторого a, т. е. прямая y = a делит
площадь многоугольника пополам. Аналогично существует прямая,
перпендикулярная l и делящая площадь многоугольника пополам. Эти две
прямые разбивают многоугольник на части, площади которых
равны S1,S2,S3 и S4 (рис. 4.13). Так как S1 + S2 = S3 + S4
и S1 + S4 = S2 + S3, то S1 = S3 = A и S2 = S4 = B. При
повороте прямой l на 90° A заменится на B, а B-
на A. Так как A и B изменяются при повороте l непрерывно, то
для некоторого положения прямой A = B, т. е. площади всех четырех
фигур равны.
-
4.39.
-
а) Пусть прямая, делящая пополам площадь и периметр
треугольника ABC, пересекает стороны AC и BC в точках P и Q
соответственно. Обозначим центр вписанной окружности треугольника ABC
через O, радиус вписанной окружности через r.
Тогда SABQOP = r(AP + AB + BQ)/2 и SOQCP = r(QC + CP)/2. Так как
прямая PQ делит периметр пополам, то AP + AB + BQ = QC + CP,
поэтому SABQOP = SOQCP. Кроме того, SABQP = SQCP по
условию. Поэтому SOQP = 0, т. е. прямая QP проходит через
точку O.
б) Доказательство проводится аналогично.
-
4.40.
-
Рассматривая образ окружности S2 при симметрии
относительно центра окружности S1 и учитывая равенство площадей,
можно доказать, что диаметр AA1 окружности S1 пересекает S2
в некоторой точке K, отличной от A, причем AK > A1K. Окружность
радиуса KA1 с центром K касается окружности S1 в точке A1,
поэтому BK > A1K, т. е. BK + KA > A1A. Ясно также, что сумма длин
отрезков BK и KA меньше длины дуги S2, соединяющей точки A
и B.
-
4.41.
-
Случай, когда точка O принадлежит G, очевиден;
поэтому будем предполагать, что O не принадлежит G.
Пусть Gў- образ кривой G при симметрии относительно
точки O. Если кривые G и Gў не пересекаются, то части, на
которые G делит квадрат, не могут быть равной площади.
Пусть X- точка пересечения G и Gў, а точка Xў
симметрична X относительно точки O. Так как при симметрии
относительно точки O кривая Gў переходит в G, то Xў
принадлежит G. Поэтому прямая XXў искомая.
-
4.42.
-
Пусть площади треугольников APB,BPC,CPD и DPA
равны S1,S2,S3 и S4.
Тогда a/p = (S3 + S4)/S3 и b · CD/2 = S3 + S2,
а значит, ab · CD/2p = (S3 + S4)(S3 + S2)/S3.
Учитывая, что S2S4 = S1S3, получаем требуемое.
-
4.43.
-
Применяя теорему синусов к треугольникам ABC и ABD,
получаем AC = 2Rsin B и BD = 2Rsin A. Поэтому
| S = |
1
2
|
AC · BDsin j
= 2R2sin Asin Bsin j
|
.
-
4.44.
-
Так как площадь четырехугольника
равна (d1d2sin j)/2, где d1 и d2- длины диагоналей,
то остается проверить, что 2d1d2cos j
= |a2 + c2 – b2 – d2|.
Пусть O- точка пересечения диагоналей четырехугольника ABCD,
j
= РAOB. Тогда AB2 = AO2 + BO2 – 2AO · BOcos j
и BC2 = BO2 + CO2 + 2BO · COcos j.
Поэтому AB2 – BC2 = AO2 – CO2 – 2BO · ACcos j.
Аналогично CD2 – AD2 = CO2 – AO2 – 2DO · ACcos j. Складывая эти
равенства, получаем требуемое.
Замечание. Так как 16S2 = 4d12d22sin 2j
= 4d12d22 – (2d1d2cos j)2,
то 16S2 = 4d12d22 – (a2 + c2 – b2 – d2)2.
-
4.45.
-
а) Пусть AB = a, BC = b, CD = c и AD = d. Ясно, что
S = SABC + SADC = (absin B + cdsin D)/2 и
a2 + b2 – 2abcos B = AC2 = c2 + d2 – 2cdcos D.
Поэтому
|
16S2 = 4a2b2 – 4a2b2cos 2B + 8abcdsin Bsin D + 4c2d2 – 4c2d2cos 2D, |
|
|
(a2 + b2 – c2 – d2)2 + 8abcdcos Bcos D = 4a2b2 · cos 2B + 4c2d2cos 2D. |
|
Подставляя второе равенство в первое, получаем
|
16S2 = 4(ab + cd)2 – (a2 + b2 – c2 – d2)2 – 8abcd(1 + cos Bcos D – sin Bsin D). |
|
Ясно, что
4(ab + cd)2 – (a2 + b2 – c2 – d2)2 = 16(p – a)(p – b)(p – c)(p – d)
и 1 + cos Bcos D – sin Bsin D = 2cos 2((B + D)/2).
б) Если ABCD- вписанный четырехугольник, то РB + РD = 180°, а значит, cos 2((B + D)/2) = 0.
в) Если ABCD- описанный четырехугольник, то a + c = b + d,
поэтому p = a + c = b + d и p – a = c, p – b = d, p – c = a, p – d = b.
Следовательно, S2 = abcd× ×(1 – cos 2((B + D)/2)) = abcdsin 2((B + D)/2).
Если четырехугольник ABCD вписанный и описанный одновременно,
то S2 = abcd.
-
4.46.
-
Из точки O, лежащей внутри правильного
треугольника ABC, опустим перпендикуляры OA1,OB1 и OC1 на
стороны BC,AC и AB соответственно. Пусть a- длина стороны
треугольника ABC, h- длина высоты. Ясно,
что SABC = SBCO + SACO + SABO. Следовательно, ah = a · OA1 + a · OB1 + a · OC1, т. е. h = OA1 + OB1 + OC1.
-
4.47.
-
Пусть AD = l. Тогда 2SABC = clsin (a/2),2SACD = blsin (a/2) и 2SABD = bcsin a.
Следовательно, clsin (a/2) + blsin (a/2) = bcsin a
= 2bcsin (a/2)cos (a/2).
-
4.48.
-
а) Пусть расстояния от точек A и O до прямой BC
равны h и h1.
Тогда SOBC : SABC = h1 : h = OA1 : AA1.
Аналогично SOAC : SABC = OB1 : BB1
и SOAB : SABC = OC1 : CC1. Складывая эти равенства
и учитывая, что SOBC + SOAC + SOAB = SABC, получаем требуемое.
б) Пусть расстояния от точек B и C до прямой AA1 равны db
и dc. Тогда SABO : SACO = db : dc = BA1 :
A1C.
Аналогично SACO : SBCO = AC1 : C1B
и SBCO : SABO = CB1 : B1A.
Остается перемножить эти равенства.
-
4.49.
-
Легко проверить, что отношение длин
отрезков An + k – 1Bk и An + kBk равно отношению площадей
треугольников An + k – 1OAk и AkOAn + k. Перемножая эти
равенства, получаем требуемое.
-
4.50.
-
Так как AiBiCiDi- параллелограмм и точка O
лежит на продолжении его диагонали AiCi,
то SAiBiO = SAiDiO, а значит, AiBi :
AiDi = hi : hi – 1, где hi- расстояние от точки O до
стороны AiAi + 1. Остается перемножить эти равенства
для i = 1,…,n.
-
4.51.
-
Пусть длины сторон треугольника ABC равны a,b и c,
причем a Ј b Ј c. Тогда 2b = a + c и 2SABC = r(a + b + c) = 3rb,
где r- радиус вписанной окружности. С другой стороны,
2SABC = hbb. Поэтому r = hb/3.
-
4.52.
-
Достаточно заметить, что db · AB = 2SAXB = BX · AXsin j, где j
= РAXB и dc · AC = 2SAXC = CX · AXsin j.
-
4.53.
-
Пусть r1,…,rn- радиусы вписанных окружностей
полученных треугольников, P1,…,Pn- их периметры, a
S1,…,Sn- площади. Площадь и периметр исходного
многоугольника обозначим через S и P соответственно.
Ясно, что Pi < P (см. задачу 9.27, б)). Поэтому
|
r1 + … + rn = 2 |
S1
P1
|
+ … + 2 |
Sn
Pn
|
> 2 |
S1
P
|
+ … + 2 |
Sn
P
|
= 2 |
S
P
|
= r. |
|
-
4.54.
-
Через точку N пересечения прямых BS и CM проведем
прямые Q1S1 и P1R1, параллельные прямым QS и PR
(точки P1,Q1,R1 и S1 лежат на сторонах AB,BC,CD и DA).
Пусть F и G- точки пересечения прямых PR и Q1S1,
P1R1 и QS. Так как точка M лежит на диагонали NC
параллелограмма NQ1CR1, то SFQ1QM = SMRR1G (задача 4.19), а
значит, SNQ1QG = SNFRR1. Точка N лежит на диагонали BS
параллелограмма ABQS, поэтому SAP1NS1 = SNQ1QG = SNFRR1.
Следовательно, точка N лежит на диагонали PD параллелограмма APRD.
-
4.55.
-
Пусть E и F- точки пересечения продолжений
сторон данного четырехугольника. Обозначим вершины
четырехугольника так, что E- точка пересечения продолжений
сторон AB и CD за точки B и C, F- точка пересечения
лучей BC и AD. Достроим треугольники AEF и ABD до
параллелограммов AERF и ABLD.
При гомотетии с центром A и коэффициентом 2 середина
диагонали BD, середина диагонали AC и середина отрезка EF
переходят в точки L,C и R соответственно. Поэтому достаточно
доказать, что точки L,C и R лежат на одной прямой. Именно
этот факт был доказан в предыдущей задаче.
-
4.56.
-
Достаточно проверить, что SAKO = SALO,
т. е. AO · ALsin OAL = AO · AKsin OAK. Ясно,
что AL = CB1 = BCcos C, sin OAL = cos B, AK = BC1 = BCcos B и sin OAK = cos C.
-
4.57.
-
Так как четырехугольник A1BC1M описанный, то,
во-первых, суммы длин его противоположных сторон равны:
,
а во-вторых, его вписанная окружность является одновременно
вписанной окружностью треугольников AA1B и CC1B, имеющих
к тому же равные площади, поэтому периметры этих треугольников
равны:
| c + ma + |
a
2
|
= a + mc + |
c
2
|
|
. Умножая первое равенство на 3
и складывая его со вторым, получаем требуемое.
-
4.58.
-
Докажем сначала одно общее утверждение, которым
мы воспользуемся при решении задач а)-г). Возьмем на лучах AB и AC
произвольные точки B1 и C1 и опустим из них перпендикуляры B1K
и C1L на прямую AO. Так как B1C1 і B1K + C1L,
то B1C1 · Ra і B1K · Ra + C1L · Ra = 2SAOB1 + 2SAOC1 = AB1 · dc + AC1 · db.
а) Полагая B1 = B и C1 = C, получаем требуемое.
б) Домножая обе части неравенства aRa і cdc + bdb на da/a,
получаем daRa і (c/a)dadc + (b/a)dadb. Складывая это неравенство
с аналогичными неравенствами для dbRb и dcRc и учитывая,
что
, получаем требуемое.
в) Возьмем точки B1 и C1 так, что AB1 = AC и AC1 = AB.
Тогда aRa і bdc + cdb, т. е. Ra і (b/a)dc + (c/a)db.
Складывая это неравенство с аналогичными неравенствами для Rb
и Rc и учитывая, что
, получаем требуемое.
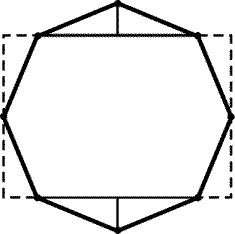
Рис. 4.14
г) Возьмем точки B1 и C1 так, что AB1 = AC1 = 1.
Тогда B1C1 = 2sin (A/2), а значит, 2sin (A/2)Ra і dc + db.
Умножая это неравенство на аналогичные неравенства для Rb и Rc и
учитывая, что sin (A/2)sin (B/2)sin (C/2) = r/4R (задача 12.36, а)),
получаем требуемое.
4.59. Отрежем от правильного восьмиугольника треугольники
и переставим их так, как показано на рис. 4.14. В результате получим
прямоугольник, стороны которого равны наибольшей и наименьшей
диагоналям восьмиугольника.
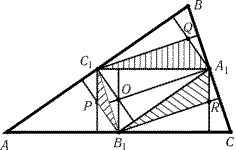
Рис. 4.15
4.60. Пусть A1,B1 и C1- середины сторон BC,CA
и AB треугольника ABC. Проведенные отрезки являются высотами
треугольников AB1C1, A1BC1 и A1B1C. Пусть P,Q и R-
точки пересечения высот этих треугольников, а O- точка
пересечения высот треугольника A1B1C1 (рис. 4.15). Рассматриваемый
шестиугольник состоит из треугольника A1B1C1 и
треугольников B1C1P, C1A1Q и A1B1R. Ясно, что
DB1C1P = DC1B1O,DC1A1Q = DA1C1O
и DA1B1R = DB1A1O. Поэтому площадь
рассматриваемого шестиугольника равна удвоенной площади
треугольника A1B1C1. Остается заметить,
что SABC = SA1B1C1.
4.61. а) Отрежем от параллелограмма две части (рис. 4.16, а )
и переставим их так, как показано на рис. 4.16, б . Получится фигура,
состоящая из mn + 1 маленьких параллелограммов. Поэтому площадь
маленького параллелограмма равна 1/(mn + 1).
б) Отрежем от параллелограмма три части (рис. 4.17, а ) и переставим
их так, как показано на рис. 4.17, б . Получится фигура,
состоящая из mn – 1 маленьких параллелограммов. Поэтому площадь
маленького параллелограмма равна 1/(mn – 1).
4.62. а) Разрежем исходный квадрат на четыре квадрата и
рассмотрим один из них (рис. 4.18). Пусть точка Bў симметрична
точке B относительно прямой PQ. Докажем, что D
APB = DOBўP. Треугольник APB равнобедренный, причем
угол при его основании равен 15°, поэтому
треугольник BPQ равносторонний. Следовательно,
Рис. 4.18
РOPBў = РOPQ – РBўPQ = 75° – 60° = 15° и РPOBў = РPOQ/2 = 15°. Кроме того, AB = OP. Аналогично
доказывается, что DBQC = DOBўQ. Следовательно,
площадь заштрихованной на рис. 4.7 части равна площади
треугольника OPQ.
б) Пусть площадь правильного двенадцатиугольника, вписанного
в окружность радиуса 1, равна 12x. Согласно задаче а) площадь
квадрата, описанного около этой окружности, равна 12x + 4x = 16x;
с другой стороны, площадь этого квадрата равна 4, поэтому x = 1/4
и 12x = 3.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:47.

 Глава 4. Задачи для самостоятельного решения |
Глава 4. Задачи для самостоятельного решения | 

 Глава 4. Задачи для самостоятельного решения |
Глава 4. Задачи для самостоятельного решения | 

