Глава 5. § 6  |	Оглавление |	Глава 5. § 8

§ 7.  Теорема Менелая

Пусть 

® AB

и 

® CD

- коллинеарные векторы. Обозначим через 

AB CD

величину 

±

AB CD

, где знак плюс берется в том случае, когда векторы 

® AB

и 

® CD

сонаправлены, а знак минус- в случае, когда векторы 

® AB

и 

® CD

направлены в разные стороны.

5.64^*.

На сторонах BC,CA и AB треугольника ABC (или на их продолжениях) взяты точки A₁,B₁ и C₁ соответственно. Докажите, что точки A₁,B₁ и C₁ лежат на одной прямой тогда и только тогда, когда

BA1 CA1  ·  CB1 AB1  ·  AC1 BC1  = 1       (теорема Менелая ).

5.65^*.

Решите задачу 5.95, а) с помощью теоремы Менелая.

5.66^*.

Окружность S касается окружностей S₁ и S₂ в точках A₁ и A₂. Докажите, что прямая A₁A₂ проходит через точку пересечения общих внешних или общих внутренних касательных к окружностям S₁ и S₂.

5.67^*.

а) Серединный перпендикуляр к биссектрисе AD треугольника ABC пересекает прямую BC в точке E. Докажите, что BE : CE = c² : b².

5.68^*.

Из вершины C прямого угла треугольника ABC опущена высота CK, и в треугольнике ACK проведена биссектриса CE. Прямая, проходящая через точку B параллельно CE, пересекает CK в точке F. Докажите, что прямая EF делит отрезок AC пополам.

5.69^*.

На прямых BC,CA и AB взяты точки A₁,B₁ и C₁, причем точки A₁,B₁ и C₁ лежат на одной прямой. Прямые, симметричные прямым AA₁,BB₁ и CC₁ относительно соответствующих биссектрис треугольника ABC, пересекают прямые BC,CA и AB в точках A₂,B₂ и C₂. Докажите, что точки A₂,B₂ и C₂ лежат на одной прямой.

5.70^*.

Прямые AA₁,BB₁,CC₁ пересекаются в одной точке O. Докажите, что точки пересечения прямых AB и A₁B₁,  BC и B₁C₁,  AC и A₁C₁ лежат на одной прямой (Дезарг).

5.71^*.

На одной прямой взяты точки A₁, B₁ и C₁, а на другой- точки A₂,B₂ и C₂. Прямые A₁B₂ и A₂B₁,  B₁C₂ и B₂C₁,  C₁A₂ и C₂A₁ пересекаются в точках C,A и B соответственно. Докажите, что точки A,B и C лежат на одной прямой (Папп).

5.72^*.

На сторонах AB,BC и CD четырехугольника ABCD (или на их продолжениях) взяты точки K,L и M. Прямые KL и AC пересекаются в точке P,  LM и BD- в точке Q. Докажите, что точка пересечения прямых KQ и MP лежит на прямой AD.

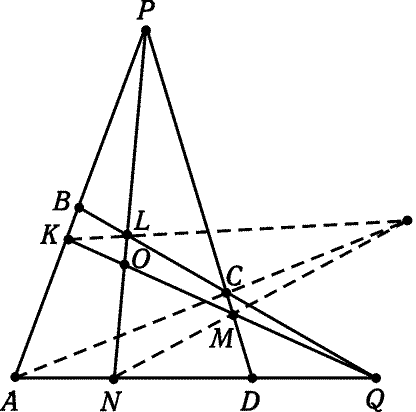
Рис. 5.2

5.73^* Продолжения сторон AB и CD четырехугольника ABCD пересекаются в точке P, а продолжения сторон BC и AD- в точке Q. Через точку P проведена прямая, пересекающая стороны BC и AD в точках E и F. Докажите, что точки пересечения диагоналей четырехугольников ABCD, ABEF и CDFE лежат на прямой, проходящей через точку Q.

                      5.74^*. а) Через точки P и Q проведены тройки прямых. Обозначим их точки пересечения так, как показано на рис. 5.2. Докажите, что прямые KL,AC и MN пересекаются в одной точке (или параллельны).

                      б) Докажите, далее, что если точка O лежит на прямой BD, то точка пересечения прямых KL,AC и MN лежит на прямой PQ.

5.75^*. На прямых BC,CA и AB взяты точки A₁,B₁ и C₁. Пусть P₁- произвольная точка прямой BC, P₂- точка пересечения прямых P₁B₁ и AB, P₃- точка пересечения прямых P₂A₁ и CA, P₄- точка пересечения P₃C₁ и BC и т. д. Докажите, что точки P₇ и P₁ совпадают.

5.76^*. Диагонали AB, BE и CF шестиугольника ABCDEF пересекаются в одной точке. Пусть Aў - точка пересечения прямых AC и FB, Bў - точка пересечения BD и AC, Cў - точка пересечения CE и BD. Докажите, что точки пересечения прямых AўBў и DўEў, BўCў и EўFў, CўDў и FўAў лежат на одной прямой.

См. также задачу 6.104.

Глава 5. § 6  |	Оглавление |	Глава 5. § 8

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.