Глава 6 |	Оглавление |	Глава 6. § 2

§ 1.  Вписанные и описанные четырехугольники

6.1.

Докажите, что если центр вписанной в четырехугольник окружности совпадает с точкой пересечения диагоналей, то этот четырехугольник- ромб.

6.2.

Четырехугольник ABCD описан около окружности с центром O. Докажите, что РAOB + РCOD = 180°.

6.3.

Докажите, что если существует окружность, касающаяся всех сторон выпуклого четырехугольника ABCD, и окружность, касающаяся продолжений всех его сторон, то диагонали такого четырехугольника перпендикулярны.

6.4.

Окружность высекает на всех четырех сторонах четырехугольника равные хорды. Докажите, что в этот четырехугольник можно вписать окружность.

6.5.

Докажите, что если в четырехугольник можно вписать окружность, то центр этой окружности лежит на одной прямой с серединами диагоналей.

6.6.

Четырехугольник ABCD описан около окружности с центром O. В треугольнике AOB проведены высоты AA₁ и BB₁, а в треугольнике COD- высоты CC₁ и DD₁. Докажите, что точки A₁,B₁,C₁ и D₁ лежат на одной прямой.

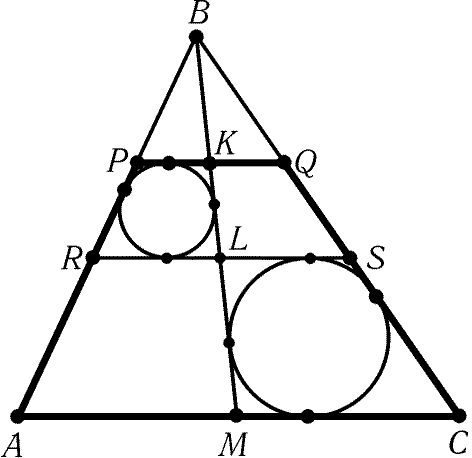
Рис. 6.1

6.7. Углы при основании AD трапеции ABCD равны 2a и 2b. Докажите, что трапеция описанная тогда и только тогда, когда BC/AD = tg atg b.

6.8. В треугольнике ABC проведены отрезки PQ и RS, параллельные стороне AC, и отрезок BM (рис. 6.1). Трапеции RPKL и MLSC описанные. Докажите, что трапеция APQC тоже описанная.

6.9^*. Дан выпуклый четырехугольник ABCD. Лучи AB и DC пересекаются в точке P, а лучи BC и AD- в точке Q. Докажите, что четырехугольник ABCD описанный тогда и только тогда, когда выполняется одно из следующих условий:  AB + CD = BC + AD, AP + CQ = AQ + CP или BP + BQ = DP + DQ.

6.10^*.

Через точки пересечения продолжений сторон выпуклого четырехугольника ABCD проведены две прямые, делящие его на четыре четырехугольника. Докажите, что если четырехугольники, примыкающие к вершинам B и D, описанные, то четырехугольник ABCD тоже описанный.

6.11^*.

На стороне BC треугольника ABC взяты точки K₁ и K₂. Докажите, что общие внешние касательные к вписанным окружностям треугольников ABK₁ и ACK₂ общие внешние касательные к вписанным окружностям треугольников ABK₂ и ACK₁ пересекаются в одной точке.

6.12^*.

Через каждую из точек пересечения продолжений сторон выпуклого четырехугольника ABCD проведено по две прямые. Эти прямые делят четырехугольник на девять четырехугольников.

б) Докажите, что если r_a, r_b, r_c, r_d - радиусы окружностей, вписанных в четырехугольники, примыкающие к вершинам A, B, C, D, то

1 ra  +   1 rc  =   1 rb  +   1 rd .

6.13^*.

Окружности S₁ и S₂, S₂ и S₃, S₃ и S₄, S₄ и S₁ касаются внешним образом. Докажите, что четыре общие касательные (в точках касания окружностей) либо пересекаются в одной точке, либо касаются одной окружности.

6.14^*.

Докажите, что точка пересечения диагоналей описанного четырехугольника совпадает с точкой пересечения диагоналей четырехугольника, вершинами которого служат точки касания сторон исходного четырехугольника с вписанной окружностью.

6.15^*.

Четырехугольник ABCD вписанный;  H_c и H_d- ортоцентры треугольников ABD и ABC. Докажите, что CDH_cH_d- параллелограмм.

6.16^*.

Четырехугольник ABCD вписанный. Докажите, что центры вписанных окружностей треугольников ABC, BCD, CDA и DAB образуют прямоугольник.

6.17^*.

Продолжения сторон четырехугольника ABCD, вписанного в окружность с центром O, пересекаются в точках P и Q, а его диагонали пересекаются в точке S.

б) Докажите, что высоты треугольника PQS пересекаются в точке O.

*       *      *

6.18^*.

Диагональ AC разбивает четырехугольник ABCD на два треугольника, вписанные окружности которых касаются диагонали AC в одной точке. Докажите, что вписанные окружности треугольников ABD и BCD тоже касаются диагонали BD в одной точке, а точки их касания со сторонами четырехугольника лежат на одной окружности.

6.19^*.

Докажите, что проекции точки пересечения диагоналей вписанного четырехугольника на его стороны являются вершинами описанного четырехугольника, если только они не попадают на продолжения сторон.

6.20^*.

Докажите, что если диагонали четырехугольника перпендикулярны, то проекции точки пересечения диагоналей на стороны являются вершинами вписанного четырехугольника.

Глава 6 |	Оглавление |	Глава 6. § 2

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.