Глава 6. § 5  |	Оглавление |	Глава 6. § 7

§ 6.  Правильные многоугольники

6.56.

Число сторон многоугольника A₁… A_n нечетно. Докажите, что:

б) если этот многоугольник описанный и все его стороны равны, то он правильный.

6.57.

Все углы выпуклого многоугольника A₁… A_n равны, и из некоторой его внутренней точки O все стороны видны под равными углами. Докажите, что этот многоугольник правильный.

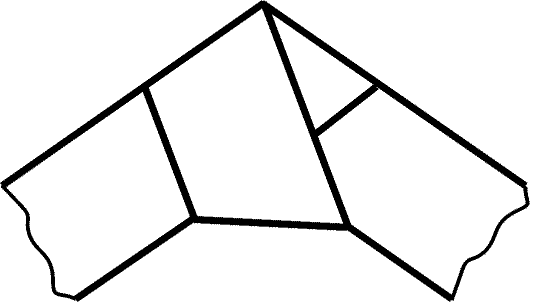
Рис. 6.3

6.58^*. Бумажная лента постоянной ширины завязана простым узлом и затем стянута так, чтобы узел стал плоским (рис. 6.3). Докажите, что узел имеет форму правильного пятиугольника.

6.59^*. На сторонах AB,BC,CD и DA квадрата ABCD построены внутренним образом правильные треугольники ABK,BCL,CDM и DAN. Докажите, что середины сторон этих треугольников (не являющихся сторонами квадрата) и середины отрезков KL,LM,MN и NK образуют правильный двенадцатиугольник.

6.60^*.

Существует ли правильный многоугольник, длина одной диагонали которого равна сумме длин двух других диагоналей?

6.61^*.

Правильный  (4k + 2)-угольник вписан в окружность радиуса R с центром O. Докажите, что сумма длин отрезков, высекаемых углом A_kOA_k + 1 на прямых  A₁A_2k,A₂A_2k – 1,…,A_kA_k + 1, равна R.

6.62^*.

В правильном восемнадцатиугольнике A₁… A₁₈ проведены диагонали A_aA_d, A_bA_e и A_cA_f. Пусть k = a – b, p = b – c,m = c – d, q = d – e, n = e – f и r = f – a. Докажите, что указанные диагонали пересекаются в одной точке в любом из следующих случаев:

б) {k,m,n} = {1,2,7} и {p,q,r} = {1,3,4};

в) {k,m,n} = {1,2,8} и {p,q,r} = {2,2,3}.

Замечание. Равенство {k,m,n} = {x,y,z} означает, что указанные наборы чисел совпадают; порядок их записи при этом не учитывается.

6.63^*.

В правильном тридцатиугольнике проведены три диагонали. Определим для них наборы {k,m,n} и {p,q,r} так же, как и в предыдущей задаче. Докажите, что если {k,m,n} = {1,3,14} и {p,q,r} = {2,2,8}, то диагонали пересекаются в одной точке.

6.64^*.

В правильном  n-угольнике (n і 3) отмечены середины всех сторон и диагоналей. Какое наибольшее число отмеченных точек лежит на одной, окружности?

6.65^*.

Вершины правильного  n-угольника окрашены в несколько цветов так, что точки одного цвета служат вершинами правильного многоугольника. Докажите, что среди этих многоугольников найдутся два равных.

6.66^*.

Докажите, что при n і 6 правильный  (n – 1)-угольник нельзя так вписать в правильный  n-угольник, чтобы на всех сторонах  n-угольника, кроме одной, лежало ровно по одной вершине  (n – 1)-угольника.

6.67.

Пусть O- центр правильного  n-угольника  A₁… A_n,  X- произвольная точка. Докажите, что 

® OA

1

+ … +

® OA

n

=

® 0

и 

® XA

1

+ … +

® XA

n

= n

® XO

.

6.68.

Докажите, что в вершинах правильного  n-угольника можно расставить действительные числа x₁,…,x_n, все отличные от нуля, так, чтобы для любого правильного  k-угольника, все вершины которого являются вершинами исходного  n-угольника, сумма чисел, стоящих в его вершинах, равнялась нулю.

6.69.

Точка A лежит внутри правильного десятиугольника X₁… X₁₀, а точка B- вне его. Пусть 

a =

® AX

1

+ … +

® AX

10

и 

b =

® BX

1

+ … +

® BX

10

. Может ли оказаться, что |a| > |b|?

6.70.

Правильный многоугольник A₁… A_n вписан в окружность радиуса R с центром O;  X- произвольная точка. Докажите, что A₁X² + … + A_nX² = n(R² + d²), где d = OX.

6.71.

Найдите сумму квадратов длин всех сторон и диагоналей правильного  n-угольника, вписанного в окружность радиуса R.

6.72.

Докажите, что сумма расстояний от произвольной точки X до вершин правильного  n-угольника будет наименьшей, если X- центр  n-угольника.

6.73.

Правильный  n-угольник  A₁… A_n вписан в окружность радиуса R с центром O;  

ei =

® OA

i

,xi =

® OX

- произвольный вектор. Докажите, что 

е

(ei,x)2 = nR2 · OX2/2

.

6.74.

Найдите сумму квадратов расстояний от вершин правильного  n-угольника, вписанного в окружность радиуса R, до произвольной прямой, проходящей через центр многоугольника.

6.75.

Расстояние от точки X до центра правильного  n-угольника равно d,  r- радиус вписанной окружности  n-угольника. Докажите, что сумма квадратов расстояний от точки X до прямых, содержащих стороны  n-угольника, равна n(r² + d²/2).

6.76.

Докажите, что сумма квадратов длин проекций сторон правильного  n-угольника на любую прямую равна na²/2, где a- сторона  n-угольника.

6.77^*.

Правильный  n-угольник  A₁… A_n вписан в окружность радиуса R;  X- точка этой окружности. Докажите, что XA₁⁴ + … + XA_n⁴ = 6nR⁴.

6.78^*.

а) Правильный  n-угольник  A₁… A_n вписан в окружность радиуса 1 с центром O;  

ei =

® OA

i

,  u - произвольный вектор. Докажите, что 

е

(u,ei)ei = nu/2

.

6.79^*.

Докажите, что если число n не является степенью простого числа, то существует выпуклый  n-угольник со сторонами длиной 1,2,…,n, все углы которого равны.

Глава 6. § 5  |	Оглавление |	Глава 6. § 7

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.