| Прасолов В. В. Задачи по планиметрии.
(4-е изд. — Осторожно! В этом издании немало опечаток!) | МЦНМО, 2002 |
|---|
-
8.1.
-
Построим отрезок BC длины a. Центр O описанной
окружности треугольника ABC является точкой пересечения двух
окружностей радиуса R с центрами в точках B и C. Выберем одну из
этих точек пересечения и построим описанную окружность S
треугольника ABC. Точка A является точкой пересечения окружности S
к прямой, параллельной прямой BC и отстоящей от нее на
расстояние ha (таких прямых две).
-
8.2.
-
Построим точки A1 и B1 на сторонах BC
и AC соответственно так, что BA1 : A1C = 1 : 3
и AB1 : B1C = 1 : 2. Пусть точка X лежит внутри
треугольника ABC. Ясно, что SABX : SBCX = 1 :
2 тогда и только тогда, когда точка X лежит на
отрезке BB1, и SABX : SACX = 1 : 3 тогда и
только тогда, когда точка X лежит на отрезке AA1. Поэтому
искомая точка M является точкой пересечения отрезков AA1
и BB1.
-
8.3.
-
Пусть O — центр данной окружности, AB —
хорда, проходящая через точку P, M — середина AB.
Тогда |AP – BP| = 2PM. Так как РPMO = 90°, точка M
лежит на окружности S с диаметром OP. Построим хорду PM
окружности S так, что PM = a/2 (таких хорд две). Искомая хорда
задается прямой PM.
-
8.4.
-
Пусть R — радиус данной окружности, O — ее
центр. Центр искомой окружности лежит на окружности S
радиуса |R ± r|
с центром O. С другой стороны, ее центр лежит на прямой l,
параллельной данной прямой и удаленной от нее на расстояние r (таких
прямых две). Любая точка пересечения окружности S и прямой l может
служить центром искомой окружности.
-
8.5.
-
Пусть R — радиус окружности S, O — ее центр.
Если окружность S высекает на прямой, проходящей через точку A,
хорду PQ и M — середина PQ, то OM2 = OQ2 – MQ2 = R2 – d2/4.
Поэтому искомая прямая касается окружности радиуса
с
центром O.
-
8.6.
-
Возьмем на прямых AB и CD точки E и F так, чтобы
прямые BF и CE имели заданные направления. Рассмотрим
всевозможные параллелограммы PQRS с заданными направлениями сторон,
вершины P и R которых лежат на лучах BA и CD, а
вершина Q — на стороне BC (рис. 8.1). Докажем, что геометрическим
местом вершин S является отрезок EF. В самом деле,
|
SR
EC
|
= |
PQ
EC
|
= |
BQ
BC
|
= |
FR
FC
|
|
, т. е.
точка S
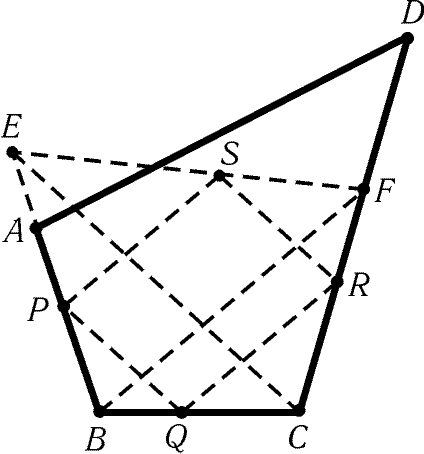
Рис. 8.1
лежит на отрезке EF. Обратно, если точка Sў лежит на
отрезке EF, то проведем SўPў||BF, PўQў||EC и QўRў||BF
(Pў, Qў, Rў- точки на прямых AB, BC, CD). Тогда
|
SўPў
BF
|
= |
PўE
BE
|
= |
QўC
BC
|
= |
QўRў
BF
|
|
, т. е.
SўPў = QўRў и PўQўRўSў- параллелограмм.
Из этого вытекает следующее построение. Строим сначала точки E
и F. Вершина S является точкой пересечения отрезков AD и EF.
Дальнейшее построение очевидно.
8.7. Предположим, что треугольник ABC построен. Пусть A1
и C1- середины сторон CB и AB. Так как C1A1||AC, то
РA1C1B = РA. Из этого вытекает, следующее построение.
Построим сначала отрезок CB длиной a и его середину A1.
Точка C1 является точкой пересечения окружности радиуса mc с
центром C и дуг окружностей, из которых отрезок A1B виден под
углом A. Построив точку C1, отложим на луче BC1
отрезок BA = 2BC1. Тогда A — искомая вершина треугольника.
-
8.8.
-
Предположим, что искомый треугольник построен и C —
вершина его прямого угла. Так как РACB = 90°, точка C
лежит на окружности S с диаметром AB. Поэтому точка C является
точкой пересечения окружности S и данной окружности. Построив
точку C и проведя прямые CA и AB, найдем оставшиеся вершины
искомого треугольника.
-
8.9.
-
Предположим, что прямоугольник ABCD построен. Опустим
из точки P перпендикуляр PR на прямую BC. Точку R можно
построить, так как она лежит на окружности с диаметром PQ
и PR = AB = a. Построив точку R, строим прямые BC и AD
и опускаем на них перпендикуляры из точек M и N.
-
8.10.
-
Предположим, что треугольник ABC построен, AH —
высота, AD — биссектриса, AM — медиана. Согласно
задаче 2.68 точка D лежит между M и H. Точка E пересечения
прямой AD и перпендикуляра, проведенного из точки M к стороне BC,
лежит на описанной окружности треугольника ABC. Поэтому центр O
описанной окружности лежит на пересечении серединного перпендикуляра
к отрезку AE и перпендикуляра к стороне BC, проведенного через
точку M.
Последовательность построений такова: на произвольной прямой
(которая в дальнейшем окажется прямой BC) строим точку H,
затем последовательно строим точки A,D,M,E,O. Искомые
вершины B и C треугольника ABC являются точками пересечения
исходной прямой с окружностью радиуса OA с центром O.
-
8.11.
-
Предположим, что треугольник ABC построен и O —
центр его вписанной окружности. Тогда РBOC = 90° + РA/2 (задача 5.3). Из точки O отрезок BC виден под
углом 90° + РA/2, и она удалена на расстояние r от
прямой BC, поэтому ее можно построить. Затем строим вписанную
окружность и проводим к ней касательные из точек B и C.
-
8.12.
-
Построим произвольный треугольник с углами A и B и
найдем его периметр P1. Искомый треугольник подобен построенному
треугольнику с коэффициентом P/P1.
-
8.13.
-
Предположим, что треугольник ABC построен.
Пусть AA1, BB1 и CC1- его медианы, M — точка их
пересечения, Mў - точка, симметричная M относительно
точки A1. Тогда MMў = 2ma/3, MC = 2mc/3 и MўC = 2mb/3, поэтому
треугольник MMўC можно построить. Точка A симметрична Mў
относительно точки M, а точка B симметрична C относительно
середины отрезка MMў.
-
8.14.
-
Ясно, что
| BC : AC : AB = |
S
ha
|
: |
S
hb
|
: |
S
hc
|
= |
1
ha
|
: |
1
hb
|
: |
1
hc
|
|
.
Возьмем произвольный отрезок BўCў и построим треугольник AўBўCў
так, чтобы BўCў : AўCў = hb : ha
и BўCў : AўBў = hc : ha. Пусть haў- высота
треугольника AўBўCў, опущенная из вершины Aў. Искомый треугольник
подобен треугольнику AўBўCў с коэффициентом ha/haў.
-
8.15.
-
Возьмем на стороне AB произвольную точку Kў, опустим
из нее перпендикуляр KўLў на сторону BC, а затем построим
квадрат KўLўMўNў, лежащий внутри угла ABC. Пусть прямая BNў
пересекает сторону AC в точке N. Ясно, что искомый квадрат
является образом квадрата KўLўMўNў при гомотетии с центром B
и коэффициентом BN : BNў.
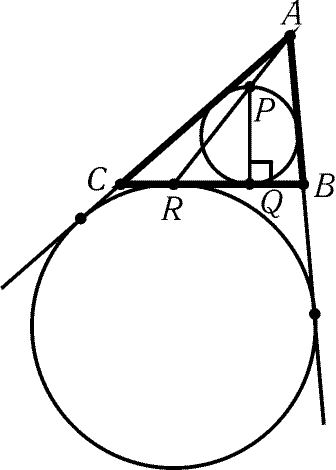
Рис. 8.2
8.16. Предположим, что искомый треугольник ABC построен.
Пусть Q — точка касания вписанной окружности со стороной BC,
PQ — диаметр этой окружности, R — точка касания вневписанной
окружности со стороной BC. Ясно, что BR = (a + b + c)/2 – c = (a + b – c)/2
и BQ = (a + c – b)/2. Поэтому RQ = |BR – BQ| = |b – c|. Вписанная окружность
треугольника ABC и вневписанная окружность, касающаяся стороны BC,
гомотетичны с центром гомотетии A. Поэтому точка A лежит на
прямой PR (рис. 8.2).
Из этого вытекает следующее построение. Строим прямоугольный
треугольник PQR по известным катетам PQ = 2r и RQ = |b – c|. Затем
проводим две прямые, параллельные прямой RQ и удаленные от
нее на расстояние ha. Вершина A является точкой пересечения одной
из этих прямых с лучом RP. Так как длина диаметра PQ вписанной
окружности известна, ее можно построить. Точки пересечения
касательных к этой окружности, проведенных из точки A, с прямой RQ
являются вершинами B и C треугольника.
8.17. Предположим, что треугольник ABC построен. Пусть
M — точка пересечения медиан AA1 и BB1. Тогда AM = 2ma/3
и BM = 2mb/3. Треугольник ABM можно построить по длинам
сторон AB = c, AM и BM. Затем на лучах AM и BM откладываем
отрезки AA1 = ma и BB1 = mb. Вершина C является точкой пересечения
прямых AB1 и A1B.
-
8.18.
-
Предположим, что треугольник ABC построен. Пусть
H — основание высоты, опущенной из вершины A. Прямоугольный
треугольник ACH можно построить по гипотенузе AC = b и
катету AH = ha. Затем на прямой CH строим точку B так, что CB = a.
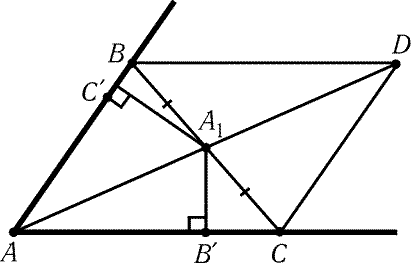
Рис. 8.3
8.19. Предположим, что треугольник ABC построен. Опустим
из середины A1 стороны BC перпендикуляры A1Bў и A1Cў на
прямые AC и AB соответственно. Ясно, что AA1 = ma, A1Bў = hb/2
и A1Cў = hc/2. Из этого вытекает следующее построение. Строим
отрезок AA1 длиной ma. Затем строим прямоугольные
треугольники AA1Bў и AA1Cў по известным катетам и гипотенузе так,
чтобы они лежали по разные стороны от прямой AA1. Остается
построить точки B и C на сторонах ACў и ABў угла CўABў так,
чтобы отрезок BC делился точкой A1 пополам. Для этого отложим на
луче AA1 отрезок AD = 2AA1, а затем проведем через точку D
прямые, параллельные сторонам угла CўABў. Точки пересечения этих
прямых со сторонами угла CўABў являются вершинами искомого
треугольника (рис. 8.3).
-
8.20.
-
Построим угол BўACў, равный РA. Точка B
строится как пересечение луча ABў и прямой, параллельной лучу ACў и
удаленной от него на расстояние hb. Аналогично строится точка C.
-
8.21.
-
Предположим, что треугольник ABC построен. Опустим
из точки B высоту BH и проведем медиану BB1. В прямоугольных
треугольниках CBH и B1BH известны катет BH и гипотенузы CB
и BB1, поэтому их можно построить. Затем на луче CB1 откладываем
отрезок CA = 2CB1. Задача имеет два решения, так как треугольники CBH
и B1BH можно строить либо по одну, либо по разные стороны от
прямой BH.
-
8.22.
-
Предположим, что треугольник ABC построен.
Пусть M — середина отрезка BC. Опустим из точки A высоту AH,
а из точки M — перпендикуляр MD на сторону AC. Ясно,
что MD = hb/2. Поэтому треугольники AMD и AMH можно построить.
Вершина C является точкой пересечения прямых AD и MH. На луче CM
откладываем отрезок CB = 2CM. Задача имеет два решения, так как
треугольники AMD и AMH можно строить либо по одну, либо по разные
стороны от прямой AM.
-
8.23.
-
Предположим, что треугольник ABC построен.
Пусть A1,B1 и C1- середины сторон BC,CA и AB
соответственно. В треугольнике CC1B1 известны все стороны:
CC1 = mc, C1B1 = a/2 и CB1 = b/2, поэтому его можно построить.
Точка A симметрична C относительно точки B1, а точка B
симметрична A относительно точки C1.
-
8.24.
-
Предположим, что треугольник ABC построен, AM —
его медиана, AH — высота. Пусть точка Aў симметрична A
относительно точки M.
Построим отрезок AAў = 2ma. Пусть M — его середина. Построим
прямоугольный треугольник AMH с гипотенузой AM и катетом AH = ha.
Точка C лежит на дуге окружности, из которой отрезок AAў
виден под углом 180° – РA, так как РACAў = 180° – РCAB. Поэтому точка C является точкой
пересечения этой дуги и прямой MH. Точка B симметрична C
относительно точки M.
-
8.25.
-
Предположим, что треугольник ABC построен. Пусть
CD — его биссектриса. Проведем прямую MD, параллельную
стороне BC (точка M лежит на стороне AC). Треугольник CMD
равнобедренный, так как РMCD = РDCB = РMDC. Поскольку
MC : AM = DB : AD = CB : AC = a : b и AM + MC = b,
то MC = ab/(a + b). Строим равнобедренный треугольник CMD по
основанию CD = lc и боковым сторонам MD = MC = ab/(a + b). Затем на
луче CM откладываем отрезок CA = b, а на луче, симметричном лучу CM
относительно прямой CD, откладываем отрезок CB = a.
-
8.26.
-
Предположим, что треугольник ABC построен.
Пусть S1- вневписанная окружность, касающаяся стороны BC.
Обозначим точки касания окружности S1 с продолжениями сторон AB
и AC через K и L, а точку касания S1 со стороной BC
обозначим через M. Так как AK = AL, AL = AC + CM и AK = AB + BM,
то AK = AL = p. Пусть S2- окружность радиуса ha с центром A.
Прямая BC является общей внутренней касательной к окружностям S1
и S2.
Из этого вытекает следующее построение. Строим угол KAL,
равный по величине углу A, так, что KA = LA = p. Строим
окружность S1, касающуюся сторон угла KAL в точках K и L, и
окружность S2 радиуса ha с центром в точке A. Затем проводим
общую внутреннюю касательную к окружностям S1 и S2. Точки
пересечения этой касательной со сторонами угла KAL являются
вершинами B и C искомого треугольника.
-
8.27.
-
Точки A1 к B1 лежат на окружности S с
диаметром AB. Центр O этой окружности лежит на серединном
перпендикуляре к хорде A1B1. Из этого вытекает следующее
построение. Сначала строим точку O, являющуюся точкой пересечения
серединного перпендикуляра к отрезку A1B1 и прямой l. Затем
строим окружность радиуса OA1 = OB1 с центром O. Вершины A и B
являются точками пересечения окружности S с прямой l. Вершина C
является точкой пересечения прямой AB1 и прямой BA1.
-
8.28.
-
Пусть AB = BC и A1,B1,C1- основания биссектрис
треугольника ABC. Тогда РA1C1C = РC1CA = РC1CA1,
т. е. треугольник CA1C1 равнобедренный и A1C = A1C1.
Из этого вытекает следующее построение. Через точку B1
проводим прямую l, параллельную A1C1. На прямой l строим
точку C так, что CA1 = C1A1 и РC1A1C > 90°.
Точка A симметрична точке C относительно точки B1, а вершина B
является точкой пересечения прямых AC1 и A1C.
-
8.29.
-
а) Согласно задаче 2.19, а) точки A,B и C являются
точками пересечения продолжений высот треугольника AўBўCў с его
описанной окружностью.
б) Согласно задаче 2.19, б) точки A,B и C являются точками
пересечения продолжений биссектрис углов треугольника AўBўCў с его
описанной окружностью.
-
8.30.
-
Обозначим середины сторон BC,CA,AB треугольника
через A1,B1,C1 соответственно. Поскольку BC||B1C1||BўCў
и OA1^BC, то OAў^BўCў. Аналогично OBў^AўCў
и OCў^AўBў, т. е. O — точка пересечения высот
треугольника AўBўCў. Построив точку O, проводим серединные
перпендикуляры к отрезкам OAў,OBў,OCў. Эти прямые образуют
треугольник ABC.
-
8.31.
-
Согласно задаче 5.10 наша задача совпадает с
задачей 8.29, б).
-
8.32.
-
Пусть O — центр описанной окружности, M —
середина стороны AB, H — основание высоты, опущенной из
точки C. Точка Q является серединой дуги AB, поэтому OQ^AB.
Из этого вытекает следующее построение. Сначала по трем данным
точкам строим описанную окружность S треугольника PQR. Точка C
является точкой пересечения прямой, проведенной через точку P
параллельно OQ, и окружности S. Точка M является точкой
пересечения прямой OQ и прямой RC. Прямая AB проходит через
точку M и перпендикулярна OQ.
-
8.33.
-
Согласно задаче 5.2 точки A,B и C являются
основаниями высот треугольника A1B1C1.
-
8.34.
-
Пусть H1- точка пересечения высот
треугольника ABC. Согласно задаче 5.116 OM : MH1 = 1 : 2
и точка M лежит на отрезке OH1. Поэтому можно построить
точку H1. Затем проводим прямую H1H и восставляем к этой прямой в
точке H перпендикуляр l. Опустив из точки O перпендикуляр на
прямую l, получаем точку C1, (середину отрезка AB). На луче C1M
строим точку C так, что CC1 : MC1 = 3 : 1. Точки A и B
являются точками пересечения прямой l с окружностью радиуса CO с
центром O.
-
8.35.
-
Пусть O и I — центры описанной и вписанной
окружностей, Ic- центр вневписанной окружности, касающейся
стороны AB. Описанная окружность треугольника ABC делит
отрезок IIc пополам (задача 5.120, б), а отрезок IIc делит пополам
дугу AB. Ясно также, что точки A и B лежат на окружности с
диаметром IIc. Из этого вытекает следующее построение. Строим
окружность S с диаметром IIc и окружность S1 с центром O и
радиусом OD, где D — середина отрезка IIc. Окружности S
и S1 пересекаются в точках A и B. Теперь можно построить
вписанную окружность треугольника ABC и провести к ней касательные в
точках A и B.
-
8.36.
-
Предположим, что мы построили точки X и Y на
сторонах AB и BC треугольника ABC так, что AX = BY и XY||AC.
Проведем YY1||AB и Y1C1||BC (точки Y1 и C1 лежат на
сторонах AC и AB). Тогда Y1Y = AX = BY, т. е. BYY1C — ромб
и BY1- биссектриса угла B.
Из этого вытекает следующее построение. Проводим биссектрису BY1,
затем прямую Y1Y, параллельную стороне AB (Y лежит на BC).
Точка X теперь строится очевидным образом.
-
8.37.
-
Пусть для определенности a < b. Предположим, что
треугольник ABC построен. Возьмем на стороне AC точку D так,
что РABD = РBAC. Тогда РBDC = 2РBAC и РCBD = 3РBAC – РBAC = 2РBAC, т. е. CD = CB = a. В
треугольнике BCD известны все стороны: CD = CB = a и DB = AD = b – a.
Построив треугольник BCD, проводим луч BA, не пересекающий
сторону CD, так, что РDBA = РDBC/2. Искомая вершина A
является точкой пересечения прямой CD и этого луча.
-
8.38.
-
Пусть точка Bў лежит на прямой l, проходящей через
точку B параллельно AC. Стороны треугольников ABC и ABўC
высекают на прямой, параллельной AC, равные отрезки. Поэтому
прямоугольники PўRўQўSў
и PRQS,
вписанные в треугольники ABC
и ABўC соответственно, равны, если точки R,Q,Rў и Qў лежат на
одной прямой.
Возьмем точку Bў на прямой l так,
что РBўAC = 90°. В
треугольник ABўC
прямоугольник PўRўQўSў
с данной диагональю PўQў
вписывается очевидным образом (Pў = A).
Проведя прямую RўQў, находим
вершины R и Q искомого прямоугольника.
-
8.39.
-
Предположим, что треугольник ABC построен. Пусть K
и L — точки, в которых вневписанная окружность, касающаяся
стороны BC, касается продолжений сторон AB и AC соответственно.
Так как AK = AL = p, то эту вневписанную окружность можно
построить; остается провести к построенной окружности касательную
через данную точку M.
-
8.40.
-
Пусть продолжение биссектрисы CD пересекает описанную
окружность треугольника ABC (с прямым углом C) в точке P,
PQ — диаметр описанной окружности, O — ее центр. Тогда
PD : PO = PQ : PC, т. е. PD · PC = 2R2 = mc2. Поэтому,
проведя к окружности с диаметром CD касательную длиной Ц2mc,
легко построить отрезок длиной PC. Теперь в треугольнике OPC
известны длины всех сторон.
-
8.41.
-
Построим точку K на стороне AC так, что AK = BC – AB.
Пусть точка D лежит на отрезке AC. Равенство AD + BD + AB = BC
эквивалентно равенству AD + BD = AK. Для точки D, лежащей на
отрезке AK, последнее равенство перепишется в виде AD + BD = AD + DK,
а для точки D, не лежащей на отрезке AK,- в виде AD + BD = AD – DK.
В первом случае BD = DK, а второй случай невозможен. Поэтому точка D
является точкой пересечения серединного перпендикуляра к отрезку BK и
отрезка AC.
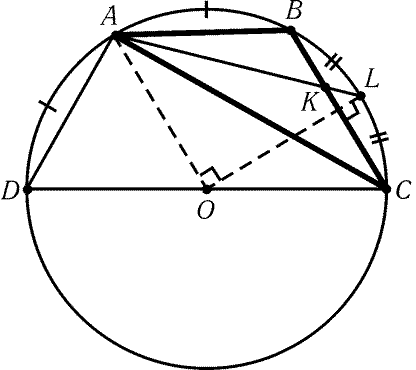
Рис. 8.4
8.42. Предположим, что треугольник ABC построен. Проведем
диаметр CD описанной окружности. Пусть O — центр описанной
окружности, L — точка пересечения продолжения биссектрисы AK
с описанной окружностью (рис. 8.4). Так как РABC – РACB = 90°, то РABD = РACB; поэтому И
DA = ИAB. Ясно также, что ИBL = ИLC. Следовательно,
РAOL = 90°.
Из этого вытекает следующее построение. Строим окружность S с
центром O и данным радиусом. На окружности S выбираем
произвольную точку A. Строим точку L на окружности S так,
что РAOL = 90°. На отрезке AL строим отрезок AK,
равный данной биссектрисе. Через точку K проводим прямую l,
перпендикулярную OL. Точки пересечения прямой l с окружностью S
являются вершинами B и C искомого треугольника ABC.
-
8.43.
-
Возьмем на сторонах BC и AC такие точки A1
и B1,
что PA1||AC и PB1||BC.
Затем отложим на лучах A1B
и B1A
отрезки A1B2 = AB1
и B1A2 = BA1.
Докажем, что
прямая A2B2 искомая.
В самом деле, пусть k = AP/AB. Тогда
|
|
B1A2
B1P
|
= |
(1 – k)a
ka
|
= |
(1 – k)a + (1 – k)b
ka + kb
|
= |
CA2
CB2
|
, |
|
т. е. DA2B1P ~ DA2CB2 и прямая A2B2
проходит через точку P. Кроме того, AA2 = |(1 – k)a – kb| = BB2.
-
8.44.
-
Предположим, что треугольник ABC построен.
Пусть B1 — точка касания вписанной окружности со стороной AC. В
прямоугольном треугольнике AOB1 известны катет OB1 = r и
гипотенуза AO, поэтому можно построить угол OAB1, а значит, и
угол BAC. Пусть O1- центр описанной окружности
треугольника ABC, M — середина стороны BC. В прямоугольном
треугольнике BO1M известны катет O1M = AH/2 (см. решение
задачи 5.116) и угол BO1M (он равен РA
или 180° – РA), поэтому его можно построить. Затем можно
определить длину отрезка
(см. задачу 5.12, а)).
Итак, можно построить отрезки длиной R и OO1 = d.
После этого возьмем отрезок AO и построим точку O1,
для которой AO1 = R и OO1 = d (таких точек может быть две).
Проведем из точки A касательные к окружности радиуса r с
центром O. Искомые точки B и C лежат на этих касательных,
удалены от точки O1 на расстояние R и, разумеется, отличны от
точки A.
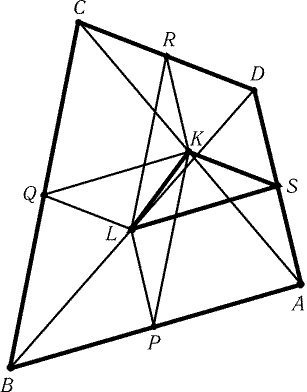
Рис. 8.5
8.45. Пусть расстояние между данными параллельными прямыми
равно a. Нужно провести через точки A и B параллельные прямые
так, чтобы расстояние между ними было равно a. Для этого
построим окружность на отрезке AB как на диаметре и найдем
точки C1 и C2 пересечения этой окружности с окружностью
радиуса a а с центром B. Сторона искомого ромба лежит на
прямой AC1 (второе решение- на прямой AC2). Затем через
точку B проводим прямую, параллельную AC1 (соответственно AC2).
8.46.
Предположим, что четырехугольник ABCD построен.
Обозначим середины сторон AB, BC, CD и DA через P,Q,R и S
соответственно и середины диагоналей AC и BD через K и L.
В треугольнике KSL известны KS = CD/2, LS = AB/2 и угол KSL,
равный углу между сторонами AB и CD. Построив треугольник KSL,
можно построить треугольник KRL, так как известны длины
всех его сторон. После этого достраиваем треугольники KSL и KRL
до параллелограммов KSLQ и KRLP. Вершины A,B,C,D являются
вершинами параллелограммов PLSA, QKPB, RLQC, SKRD (рис. 8.5).
8.47. Опустим из вершин B и D перпендикуляры BB1
и DD1 на диагональ AC. Пусть для определенности DD1 > BB1.
Построим отрезок длины a = DD1 – BB1 и проведем прямую, параллельную
прямой AC, удаленную от AC на расстояние a и пересекающую
сторону CD в некоторой точке E. Ясно, что SAED = (ED/CD)SACD = (BB1/DD1)SACD = SABC. Поэтому медиана треугольника AEC лежит на
искомой прямой.
-
8.48.
-
Пусть P,Q,R — середины равных сторон AB,BC,CD
четырехугольника ABCD. Проведем серединные перпендикуляры l1
и l2 к отрезкам PQ и QR. Поскольку AB = BC = CD, точки B и C
лежат на прямых l1 и l2 и BQ = QC.
Из этого вытекает следующее построение. Проводим серединные
перпендикуляры l1 и l2 к отрезкам PQ и QR. Затем через
точку Q проводим отрезок с концами на прямых l1 и l2 так,
чтобы Q была его серединой (см. задачу 16.15).
-
8.49.
-
Пусть даны вершины A,B и C вписанного и описанного
четырехугольника ABCD, причем AB і BC. Тогда AD – CD = AB – BC і 0, поэтому на стороне AD можно отложить отрезок DC1,
равный DC. В треугольнике AC1C известны длины сторон AC
и AC1 = AB – BC и РAC1C = 90° + РD/2 = 180° – РB/2. Так как угол AC1C тупой, треугольник AC1C
по этим элементам строится однозначно. Дальнейшее построение очевидно.
-
8.50.
-
Пусть ABCD — описанная равнобедренная трапеция с
основаниями AD и BC, причем AD > BC; C1- проекция точки C
на прямую AD. Докажем, что AB = AC1. В самом деле, если P и Q
- точки касания сторон AB и AD с вписанной окружностью, то
AB = AP + PB = AQ + BC/2 = AQ + QC1 = AC1.
Из этого вытекает следующее построение. Пусть C1- проекция
точки C на основание AD. Тогда B — точка пересечения
прямой BC и окружности радиуса AC1 с центром A. Трапеция
с AD < BC строится аналогично.
-
8.51.
-
Обозначим середины оснований AD и BC через L и N,
а середину отрезка EF через M. Точки L,O,N лежат на одной
прямой (задача 19.2). Ясно, что точка M также лежит на этой
прямой. Из этого вытекает следующее построение. Проведем через
точку K прямую l, перпендикулярную прямой OK. Основание AD
лежит на прямой l. Точка L является точкой пересечения прямой l
и прямой OM. Точка N симметрична точке L относительно точки M.
Через точку O проведем прямые, параллельные прямым EN
и FN. Точки пересечения этих прямых с прямой l являются
вершинами A и D трапеции. Вершины B и C симметричны вершинам A
и D относительно точек E и F соответственно.
-
8.52.
-
Предположим, что мы построили четырехугольник ABCD
с данными длинами сторон и данной средней линией KP (K и P —
середины сторон AB и CD). Пусть A1 и B1- точки,
симметричные точкам A и B относительно точки P.
Треугольник A1BC можно построить, так как в нем известны
стороны BC, CA1 = AD и BA1 = 2KP. Достроим треугольник A1BC до
параллелограмма A1EBC. Теперь можно построить точку D, так как
известны CD и ED = BA. Воспользовавшись тем,
что
, построим точку A.
-
8.53.
-
Используя формулы задач 6.37 и 6.38, легко выразить
диагонали вписанного четырехугольника через его стороны.
Полученные формулы можно использовать для построения диагоналей (для
удобства следует ввести произвольный отрезок e в качестве
отрезка единичной длины и строить отрезки длиной pq, p/q и Цp
как pq/e, pe/q и
).
-
8.54.
-
Окружность высекает на сторонах угла равные отрезки
тогда и только тогда, когда ее центр лежит на биссектрисе угла.
Поэтому центром искомой окружности является точка пересечения
серединного перпендикуляра к отрезку AB и биссектрисы данного угла.
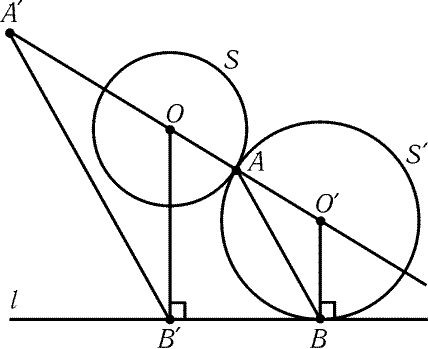
Рис. 8.6
8.55. Предположим, что мы построили окружность Sў,
касающуюся данной окружности S в точке A и данной прямой l в
некоторой точке B. Пусть O и Oў- центры окружностей S и Sў
соответственно (рис. 8.6). Ясно, что точки O,Oў и A лежат на одной
прямой и OўB = OўA. Поэтому нужно построить точку Oў на прямой OA
так, чтобы OўA = OўB, где B — основание перпендикуляра,
опущенного из точки Oў на прямую l. Для этого опустим
перпендикуляр OBў на прямую l. Затем отложим на прямой AO
отрезок OAў длины OBў. Через точку A проведем прямую AB,
параллельную AўBў (точка B лежит на прямой l). Точка Oў
является точкой пересечения прямой OA и перпендикуляра к прямой l,
проведенного через точку B.
-
8.56.
-
а) Пусть l1- серединный перпендикуляр к
отрезку AB, C — точка пересечения прямых l1 и l,
а lў- прямая, симметричная l относительно прямой l1. Задача
сводится к тому, чтобы построить окружность, проходящую через точку A
и касающуюся прямых l и lў (см. задачу 19.16).
б) Можно считать, что центр окружности S не лежит на
серединном перпендикуляре к отрезку AB (иначе построение очевидно).
Возьмем произвольную точку C окружности S и построим
описанную окружность треугольника ABC; она пересекает S в некоторой
точке D. Пусть M — точка пересечения прямых AB и CD.
Проведем к окружности S касательные MP и MQ. Тогда описанные
окружности треугольников ABP и ABQ искомые, так как MP2 = MQ2 = MA · MB.
-
8.57.
-
Предположим, что мы построили окружности S1,S2
и S3, попарно касающиеся в данных точках: S1 и S2 касаются в
точке C; S1 и S3- в точке B; S2 и S3- в
точке A. Пусть O1,O2 и O3- центры окружностей S1,S2
и S3. Тогда точки A,B и C лежат на сторонах
треугольника O1O2O3, причем O1B = O1C, O2C = O2A и O3A = O3B.
Поэтому точки A,B и C являются точками касания вписанной окружности
треугольника O1O2O3 со сторонами.
Из этого вытекает следующее построение. Строим описанную
окружность треугольника ABC и проводим к ней касательные
в точках A,B и C. Точки пересечения этих касательных являются
центрами искомых окружностей.
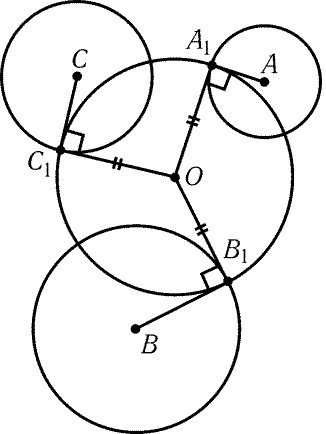
Рис. 8.7
8.58. Предположим, что мы построили окружность S,
касательные AA1,BB1 и CC1 к которой имеют длины a,b и c
соответственно (A1,B1 и C1- точки касания). Построим
окружности Sa,Sb и Sc с центрами A,B и C и радиусами a,b
и c соответственно (рис. 8.7). Если O — центр окружности S, то
отрезки OA1, OB1 и OC1 являются как радиусами окружности S,
так и касательными к окружностям Sa,Sb и Sc. Поэтому точка O
является радикальным центром окружностей Sa,Sb и Sc (см. § 10
гл. 3).
Из этого вытекает следующее построение. Сначала строим
окружности Sa,Sb и Sc. Затем строим их радикальный
центр O. Искомая окружность является окружностью с центром O и
радиусом, равным по длине касательной, проведенной из точки O к
окружности Sa.
-
8.59.
-
Построим сначала отрезок BC длиной a. Затем построим
ГМТ X, для которых CX : BX = b : c (см. задачу 7.14). В
качестве вершины A можно взять любую из точек пересечения этого ГМТ с
прямой, удаленной от прямой BC на расстояние ha.
-
8.60.
-
По длинам отрезков ADў и BD можно построить
отрезок AB и точку D на этом отрезке. Точка C является точкой
пересечения окружности радиуса CD с центром D и ГМТ X, для
которых AX : BX = AD : BD.
-
8.61.
-
Пусть X — точка, не лежащая на прямой AB. Ясно,
что РAXB = РBCX тогда и только тогда,
когда AX : CX = AB : CB. Поэтому точка M является точкой
пересечения ГМТ X, для которых AX : CX = AB : CB, и
ГМТ Y, для которых BY : DY = BC : DC (эти ГМТ могут не
пересекаться).
-
8.62.
-
Нужно построить точку O, для которой AO : AўO = AB : AўBў и BO : BўO = AB : AўBў. Точка O является
точкой пересечения ГМТ X, для которых AX : AўX = AB : AўBў,
и ГМТ Y, для которых BY : BўY = AB : AўBў.
-
8.63.
-
Пусть O — центр данной окружности. Хорды XP
и XQ, проходящие через точки A и B, равны, тогда и только тогда,
когда XO — биссектриса угла PXQ, т. е. AX : BX = AO : BO. Искомая точка X является точкой пересечения
соответствующей окружности Аполлония с данной окружностью.
-
8.64.
-
а) Если прямая l не пересекает отрезок AB,
то ABB1A1- параллелограмм и l||AB. Если прямая l
пересекает отрезок AB, то AA1BB1- параллелограмм и l
проходит через середину отрезка AB.
б) Одна из искомых прямых параллельна прямой AB, а другая
проходит через середину AB.
8.65. Построим окружность радиуса 1 и проведем в ней два
перпендикулярных диаметра AB и CD. Пусть O — центр окружности,
M — середина отрезка OC, P — точка пересечения прямой AM
и окружности с диаметром OC (рис. 8.8). Тогда
, а значит, AP = AM – PM = (Ц5 – 1)/2 = 2sin 18° (см. зада-
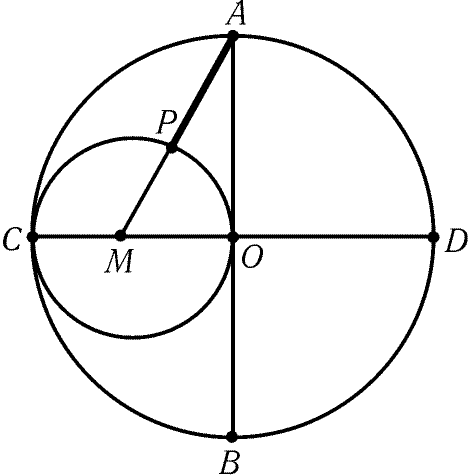
Рис. 8.8
чу 5.46), т. е. AP — длина стороны
правильного десятиугольника, вписанного в данную окружность.
8.66. Предположим, что мы построили прямоугольник PQRS так,
что данные точки A,B,C,D лежат на сторонах PQ,QR,RS,SP
соответственно и PQ : QR = a, где a — данное отношение
сторон. Пусть F — точка пересечения прямой, проведенной через
точку D перпендикулярно к прямой AC, и прямой QR.
Тогда DF : AC = a.
Из этого вытекает следующее построение. Из точки D проводим
луч, пересекающий отрезок AC под прямым углом, и на этом луче
строим точку F так, что DF = a · AC. Сторона QR лежит на
прямой BF. Дальнейшее построение очевидно.
-
8.67.
-
Предположим, что точки X и Y, обладающие требуемыми
свойствами, построены. Обозначим точку пересечения прямых AX
и YC через M, а точку пересечения прямых AB и XY через K.
Прямоугольные треугольники AXK и YXM имеют общий острый
угол X, поэтому РXAK = РXYM. Углы XAB и XYB опираются
на одну дугу, поэтому РXAB = РXYB.
Следовательно,
РXYM = РXYB.
Так как XY^AB, то A — середина
отрезка CB.
Обратно, если K — середина отрезка CB, то РMYX = РBYX = РXAB. Треугольники AXK и YXM имеют общий угол X и РXAK = РXYM, поэтому РYMX = РAKX = 90°.
Из этого вытекает следующее построение. Через середину K
отрезка CB проводим прямую l, перпендикулярную прямой AB.
Точки X и Y являются точками пересечения прямой l с данной
окружностью.
-
8.68.
-
Если есть угол величиной a, то можно построить углы
величиной 2a,3a и т. д. Так как 19 · 19° = 361, то
можно построить угол 361°, совпадающий с углом 1°.
-
8.69.
-
Построим сначала угол 36° (см. задачу 8.65).
Затем можно построить угол (36° – 30°)/2 = 3°.
Если n не делится на 3, то, имея углы n° и 3°,
можно построить угол 1°. В самом деле, если n = 3k + 1,
то 1° = n° – k · 3°, а если n = 3k + 2,
то 1° = 2n° – (2k + 1) · 3°.
-
8.70.
-
Последовательность построений такова. Выберем на клочке
бумаги произвольную точку O и произведем гомотетию с центром O
и достаточно малым коэффициентом k так, чтобы образ точки
пересечения данных прямых при этой гомотетии оказался на клочке
бумаги. Тогда можно построить биссектрису угла между образами
прямых. Затем произведем гомотетию с прежним центром и
коэффициентом 1/k и получим искомый отрезок биссектрисы.
-
8.71.
-
Построим с помощью двусторонней линейки две
параллельные хорды AB и CD. Пусть P и Q — точки пересечения
прямых AC и BD,AD и BC. Тогда прямая PQ проходит через центр
данной окружности. Построив аналогично еще одну такую прямую, найдем
центр окружности.
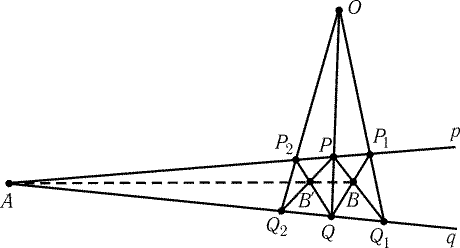
Рис. 8.9
8.72. Проведем через точку A два луча p и q, образующие
угол маленькой величины, содержащий точку B (лучи можно
построить, переставляя линейку). Через точку B проведем отрезки PQ1
и P1Q (рис. 8.9). Если PQ < 10см и P1Q1 < 10см, то
можно построить точку O, в которой пересекаются прямые PQ
и P1Q1. Проведем через точку O прямую P2Q2.
Если PQ2 < 10см и P2Q < 10см, то можно построить
точку Bў, в которой пересекаются прямые PQ2 и P2Q.
Если BBў < 10см, то можно построить прямую BBў, а эта
прямая проходит через точку A (см. задачу 5.73).
-
8.73.
-
Построение будет основано на том факте, что если A
и B — точки пересечения равных окружностей с центрами P и Q,
то
. Пусть S1 = исходная окружность, A1-
данная точка. Через точку A1 проведем окружность S2, через
точку A2 пересечения окружностей S1 и S2-
окружность S3, через точку A3 пересечения окружностей S2
и S3 — окружность S4, наконец, через точки B1 и A4
пересечения окружностей S1 и S3 с окружностью S4-
окружность S5. Докажем, что точка B2 пересечения
окружностей S5 и S1 искомая. Пусть Oi- центр
окружности Si. Тогда
|
®
A1O1
|
= |
®
O2A2
|
= |
®
A3O3
|
= |
®
O4A4
|
= |
®
B1O5
|
= |
®
O1B2
|
|
.
Замечание.
Точек пересечения окружностей S1 и S2 две; в качестве точки B1
можно выбирать любую из них.
-
8.74.
-
Пусть AB — данный отрезок, P — произвольная
точка, не лежащая на данных прямых. Построим точки C и D
пересечения второй из данных прямых с прямыми PA и PB
соответственно и точку Q пересечения прямых AD и BC. Согласно
задаче 19.2 прямая PQ проходит через середину отрезка AB.
-
8.75.
-
Пусть AB — данный отрезок, а C и D —
произвольные точки на второй данной прямой. Согласно предыдущей задаче
можно построить точку M — середину отрезка CD. Пусть P —
точка пересечения прямых AM и BD, E — точка пересечения
прямых PC и AB. Докажем, что EB — искомый отрезок.
Поскольку DPMC ~ DPAE
и DPMD ~ DPAB, то
|
|
AB
AE
|
= |
AB
AP
|
: |
AE
AP
|
= |
MD
MP
|
: |
MC
MP
|
= |
MD
MC
|
= 1. |
|
-
8.76.
-
Пусть AB — данный отрезок, а C и D — произвольные
точки на второй данной прямой. Согласно предыдущей задаче можно
построить такие точки D1 = D,D2,…,Dn,
что все отрезки DiDi + 1
равны отрезку CD. Пусть P — точка пересечения прямых AC
и BDn, а B1,…,Bn – 1- точки пересечения прямой AB с
прямыми PD1,…,PDn – 1 соответственно. Ясно, что
точки B1,…,Bn – 1 делят отрезок AB на n равных частей.
-
8.77.
-
Возьмем на одной из данных прямых отрезок AB и
построим его середину M (см. задачу 8.74). Пусть A1 и M1-
точки пересечения прямых PA и PM со второй данной прямой, Q —
точка пересечения прямых BM1 и MA1. Легко проверить, что
прямая PQ параллельна данным прямым.
-
8.78.
-
В случае, когда точка P не лежит на прямой AB,
можно воспользоваться решением задачи 3.36. Если же точка P
лежит на прямой AB, то мы можем сначала опустить перпендикуляры l1
и l2 из каких-нибудь других точек, а затем согласно задаче 8.77
провести через точку P прямую, параллельную прямым l1 и l2.
-
8.79.
-
а) Пусть A — данная точка, l — данная
прямая. Рассмотрим сначала случай, когда точка O не лежит на
прямой l. Проведем через точку O две произвольные прямые,
пересекающие прямую l в точках B и C. Согласно задаче 8.78 в
треугольнике OBC можно опустить высоты на стороны OB и OC. Пусть
H — точка их пересечения. Тогда можно провести прямую OH,
которая перпендикулярна l. Согласно задаче 8.78 можно опустить
перпендикуляр из точки A на OH. Это и есть искомая прямая,
проходящая через A и параллельная l. Чтобы из A опустить
перпендикуляр на l, нужно восставить из O перпендикуляр lў
к OH, а затем из A опустить перпендикуляр на lў. В случае, когда
точка O лежит на прямой l, согласно задаче 8.78 можно сразу
опустить из точки A перпендикуляр lў на прямую l, а затем из той
же точки A восставить перпендикуляр к прямой lў.
б) Пусть l — данная прямая, A — лежащая на ней данная точка
и BC — данный отрезок. Проведем через точку O прямые OD и OE,
параллельные прямым l и BC соответственно (D и E — точки
пересечения этих прямых с окружностью S). Через точку C проведем
прямую, параллельную OB, до пересечения с прямой OE в точке F,
через F — прямую, параллельную ED, до пересечения с OD
в точке G и, наконец, через G — прямую, параллельную OA, до
пересечения с I в точке H. Тогда AH = OG = OF = BC, т. е. AH —
требуемый отрезок.
в) Возьмем две произвольные прямые, пересекающиеся в точке P. Отложим
на одной из них отрезок PA = a, а на другой- отрезки PB = b
и PC = c. Пусть D — точка пересечения прямой PA с прямой,
проходящей через B и параллельной AC. Ясно, что PD = ab/c.
г) Пусть H — гомотетия (или параллельный перенос), переводящая
окружность с центром A и радиусом r в окружность S (т. е.
в заданную окружность с отмеченным центром O). Так как радиусы
обеих окружностей известны, можно построить образ любой точки X
при отображении H. Для этого нужно через точку O провести
прямую, параллельную прямой AX, и отложить на ней отрезок,
равный rS · AX/r, где rS- радиус окружности S.
Аналогично строится образ любой точки при отображении H – 1. Поэтому
можно построить прямую lў = H(l) и найти точки ее пересечения с
окружностью S, а затем построить образы этих точек при
отображении H – 1.
д) Пусть A и B — центры данных окружностей, C — одна из
точек, которые нужно построить, CH — высота треугольника ABC.
Записав теорему Пифагора для треугольников ACH и BCH, получим,
что AH = (b2 + c2 – a2)/2c. Величины a,b и c известны, поэтому
можно построить точку H и точки пересечения прямой CH с одной
из данных окружностей.
-
8.80.
-
а) Проведем прямые, параллельные прямым OA и OB,
удаленные от последних на расстояние a и пересекающие стороны
угла. Точка пересечения этих прямых лежит на искомой биссектрисе.
б) Проведем прямую, параллельную OB, удаленную от последней
на расстояние a и пересекающую луч OA в некоторой точке M.
Через точки O и M проведем другую пару параллельных прямых,
расстояние между которыми равно a; прямая, проходящая через
точку O, содержит искомую сторону угла.
-
8.81.
-
Проведем через точку A произвольную прямую, а затем
проведем прямые l1 и l2, параллельные ей и удаленные от нее на
расстояние a; эти прямые пересекают прямую l в точках M1 и M2.
Через точки A и M1 проведем еще одну пару параллельных
прямых la
и lm, расстояние между которыми равно a. Точка пересечения
прямых l2 и lm лежит на искомом перпендикуляре.
-
8.82.
-
Проведем прямую, параллельную данной и удаленную от
нее на расстояние a. Теперь можно воспользоваться результатами
задач 8.77 и 8.74.
-
8.83.
-
Проведем через точку P прямые PA1||OA
и PB1||OB. Пусть прямая PM делит пополам угол между прямыми l
и PA1. При симметрии относительно прямой PM прямая PA1
переходит в прямую l, поэтому прямая PB1 при этой симметрии
переходит в одну из искомых прямых.
-
8.84.
-
Достроим треугольник ABM до параллелограмма ABMN.
Проведем через точку N прямые, параллельные биссектрисам углов
между прямыми l и MN. Точки пересечения этих прямых с прямой l
искомые.
-
8.85.
-
Проведем прямую l1, параллельную прямой OA и
удаленную от нее на расстояние a. Возьмем на прямой l произвольную
точку B. Пусть B1- точка пересечения прямых OB и l1.
Проведем через точку B1 прямую, параллельную AB; эта прямая
пересекает прямую OA в точке A1. Проведем теперь через точки O
и A1 пару параллельных прямых, расстояние между которыми равно a
(таких пар прямых может быть две); пусть X и X1- точки
пересечения прямой, проходящей через точку O, с прямыми l и l1.
Так как OA1 = OX1
и DOA1X1 ~ OAX, точка X искомая.
-
8.86.
-
Восставим в точках O1 и O2 перпендикуляры к
прямой O1O2 и отложим на них отрезки O1B1 = O2A2
и O2B2 = O1A1. Построим середину M отрезка B1B2 и в точке M
восставим перпендикуляр к B1B2. Этот перпендикуляр пересечет
прямую O1O2 в точке N. Тогда
O1N2 + O1B12 = O2N2 + O2B22, а значит,
O1N2 – O1A12 = O2N2 – O2A22, т. е. точка N лежит на
радикальной оси. Остается восставить перпендикуляр к O1O2 в
точке N.
-
8.87.
-
Построим сначала произвольную прямую l1,
перпендикулярную прямой l, а затем через точку A проведем прямую,
перпендикулярную прямой l1.
-
8.88.
-
а) Проведем через точки A и B прямые AP и BQ,
перпендикулярные прямой AB, а затем проведем произвольный
перпендикуляр к прямой AP. В результате получим прямоугольник.
Остается опустить из точки пересечения его диагоналей перпендикуляр
на прямую AB.
б) Восставим из точки B перпендикуляр l к прямой AB и проведем
через точку A две перпендикулярные прямые; они пересекают прямую l
в точках M и N. Достроим прямоугольный треугольник MAN до
прямоугольника MANR. Основание перпендикуляра, опущенного из точки R
на прямую AB, является искомой точкой C.
-
8.89.
-
а) Опустим из точки A перпендикуляр AP на прямую OB
и построим отрезок AC, серединой которого является точка P.
Тогда угол AOC искомый.
б) Возьмем на прямой OB такие точки B и B1, что OB = OB1.
Расположим прямой угол так, чтобы его стороны проходили через
точки B и B1, а вершина лежала на луче OA. Если A — вершина
прямого угла, то угол AB1B искомый.
-
8.90.
-
Проведем через точку O прямую lў, параллельную
прямой l. Из точки B опустим перпендикуляры BP и BQ на
прямые lў и OA, а затем из точки O опустим перпендикуляр OX на
прямую PQ. Тогда прямая XO искомая (см. задачу 2.3); если точка Y
симметрична точке X относительно прямой lў, то прямая YO тоже
искомая.
-
8.91.
-
Достроим треугольник OAB до параллелограмма OABC,
а затем построим отрезок CC1, серединой которого является точка O.
Расположим прямой угол так, чтобы его стороны проходили через
точки C и C1, а вершина лежала на прямой l. Вершина прямого угла
совпадает тогда с искомой точкой X.
-
8.92.
-
Построим отрезок AB, серединой которого является
точка O, и расположим прямой угол так, чтобы его стороны проходили
через точки A и B, а вершина лежала на прямой l. Тогда вершина
прямого угла совпадет с искомой точкой.
File translated from
TEX
by
TTH,
version 3.00.
On 22 Nov 2002, 13:48.

 Глава 8. Задачи для самостоятельного решения |
Глава 8. Задачи для самостоятельного решения | 

 Глава 8. Задачи для самостоятельного решения |
Глава 8. Задачи для самостоятельного решения | 





