Прасолов В. В. Задачи по планиметрии. (4-е изд. — Осторожно! В этом издании немало опечаток!)	МЦНМО, 2002


Глава 9. § 5 \|	Оглавление \|	Глава 9. § 7

§ 6. Неравенства с площадями

9.36.: Точки M и N лежат на сторонах AB и AC треугольника ABC, причем AM = CN и AN = BM. Докажите, что площадь четырехугольника BMNC по крайней мере в три раза больше площади треугольника AMN.

9.37.

Площади треугольников ABC, A₁B₁C₁, A₂B₂C₂ равны S, S₁, S₂ соответственно, причем AB = A₁B₁ + A₂B₂, AC = A₁C₁ + A₂C₂, BC = B₁C₁ + B₂C₂. Докажите, что

S Ј 4

S₁S₂

9.38.

ABCD- выпуклый четырехугольник площади S. Угол между прямыми AB и CD равен a, угол между AD и BC равен b. Докажите, что

AB · CDsin a + AD · BCsin b Ј 2S Ј AB · CD + AD · BC.

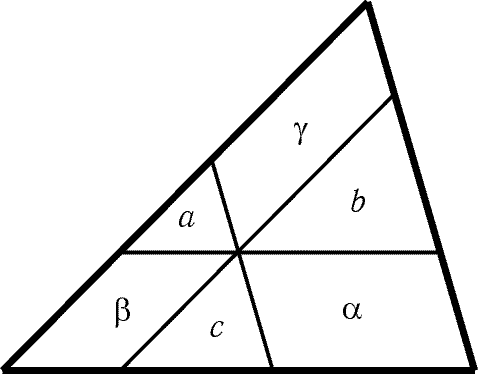
Рис. 9.1

9.39 Через точку, лежащую внутри треугольника, проведены три прямые, параллельные его сторонам. Обозначим площади частей, на которые эти прямые разбивают треугольник, так, как показано на рис. 9.1. Докажите, что a/a + b/b + c/g і 3/2.

9.40. Площади треугольников ABC и A₁B₁C₁ равны S и S₁, причем треугольник ABC не тупоугольный. Наибольшее из отношений a₁/a, b₁/b и c₁/c равно k. Докажите, что S₁ Ј k²S.

9.41. а) Точки B,C и D делят (меньшую) дугу AE окружности на четыре равные части. Докажите, что S_ACE < 8S_BCD.

б) Из точки A проведены касательные AB и AC к окружности. Через середину D (меньшей) дуги BC проведена касательная, пересекающая отрезки AB и AC в точках M и N. Докажите, что S_BCD < 2S_MAN.

9.42^*.: Все стороны выпуклого многоугольника отодвигаются во внешнюю сторону на расстояние h. Докажите, что его площадь при этом увеличится больше чем на Ph + ph², где P- периметр.

9.43^*.: Квадрат разрезан на прямоугольники. Докажите, что сумма площадей кругов, описанных около всех этих прямоугольников, не меньше площади круга, описанного около исходного квадрата.

9.44^*.: Докажите, что сумма площадей пяти треугольников, образованных парами соседних сторон и соответствующими диагоналями выпуклого пятиугольника, больше площади всего пятиугольника.

9.45^*.: а) Докажите, что в любом выпуклом шестиугольнике площади S найдется диагональ, отсекающая от него треугольник площади не больше S/6.

б) Докажите, что в любом выпуклом восьмиугольнике площади S найдется диагональ, отсекающая от него треугольник площади не больше S/8.

См. также задачу 17.19.

Глава 9. § 5 \|	Оглавление \|	Глава 9. § 7

Внимание! Данное издание содержит опечатки!
Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора.
Заказ книги: biblio@mccme.ru.