1. [Н.Х. Агаханов, Л.П. Купцов, Ю.В. Нестеренко. Всероссийские математические олимпиады. 9 класс] Книга состоит из 30 рассказов объемом 1, 2, 3,…, 30 страниц. Рассказы печатаются с первой страницы, каждый рассказ начинается с новой страницы. Какое наибольшее количество рассказов может начинаться с нечетной страницы?

Ответ: 23.

Решение. Докажем, что с нечетной страницы могут начинаться не более чем двадцать три рассказа. Действительно, после каждого рассказа с нечетным количеством страниц меняется четность начальной страницы следующего рассказа. Поэтому четность начальной страницы изменяется не менее 14 раз (один из 15 рассказов с нечетным количеством страниц может оказаться в книге последним). Таким образом, не менее семи раз рассказы начинаются с четной страницы, и тем самым не более 23 раз – с нечетной.

2. [МГУ, мехмат, 1990 г., вариант письменного вступительного экзамена] Найдите все тройки (x; y; z) целых чисел, удовлетворяющих неравенству: log₂(2x + 3y – 6z + 3) + log₂(3x – 5y + 2z – 2) + log₂(2y + 4z – 5x + 2) > z² – 9z + 17.

Ответ: {(5; 4; 4)}.

Решение. Рассмотрим область определения левой части неравенства: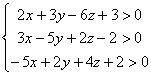 . Кроме того, сумма выражений, стоящих под знаками логарифмов равна 3. Учитывая, что эти выражения принимают только целые значения, получим, что каждое из них равно 1, то есть значение левой части равно 0.

Тогда z² – 9z + 17 < 0 Û . Так как zÎ Z, то z = 3; 4; 5; 6.

Подставляя найденные значения z в систему уравнений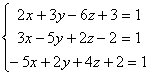 , где xÎ Z, yÎ Z, получим, что x = 5; y = 4; z = 4.

3. [XI Международный турнир городов, осенний тур, основной вариант, 10 – 11 классы] Можно ли так выбрать шар, треугольную пирамиду и плоскость, чтобы всякая плоскость, параллельная выбранной, пересекала шар и пирамиду по фигурам равной площади?

Ответ: да, можно.

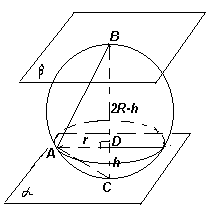
Решение. Рассмотрим шар радиуса R и две параллельные плоскости a и b , касательные к этому шару в точках С и В (см. рис. 1а). Пусть плоскость g параллельна этим плоскостям и расположена между ними на расстоянии h от плоскости a . Тогда сечением шара этой плоскостью является круг радиуса r. Из прямоугольного треугольника АВС (Ð ВАС = 90° ) r² = h(2R – h), поэтому площадь сечения равна p h(2R – h).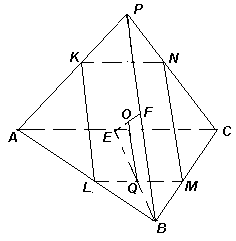

Рассмотрим тетраэдр РАВС, у которого скрещивающиеся ребра АС и РВ равны, взаимно перпендикулярны и лежат соответственно в плоскостях a и b таким образом, что отрезок ЕF, соединяющий их середины, является общим перпендикуляром к этим ребрам, то есть ЕF = 2R. Сечением тетраэдра плоскостью g является прямоугольник KLMN (см. рис. 1б). Так как и , то . Пусть РВ = АС = а, тогда KL + ML = a. Следовательно, площадь KLMN равна x(a – x), где KL = x. Так как выбранный тетраэдр симметричен относительно плоскостей РВЕ и АСF, то прямая EF их пересечения проходит через центр О прямоугольника KLMN. Пусть Q – середина ML, тогда из подобия треугольников EOQ и EFB получим, что . Следовательно, Û .

Площади сечений шара и тетраэдра должны быть равны, поэтому . Решая это уравнение, получим, что .

Таким образом, если длины ребер АС и РВ будут равны найденному значению а, то условие задачи будет выполняться.

4. [Турнир математических боев Иваново – Кострома – Ярославль, 1996 г., автор – Р.Г. Женодаров] В квадрате 100´ 100 клеток некоторые клетки закрашены. Известно, что каждая клетка (в том числе и закрашенная) граничит по стороне ровно с одной закрашенной клеткой. Сколько клеток закрашено?

Ответ: 2550.

Решение. Первый способ. Отметим часть клеток данного квадрата способом, показанным на рис. 2а для квадрата 12´ 12. Заметим, что у каждой клетки квадрата ровно два соседа отмечены. В частности, у каждой закрашенной клетки ровно два отмеченных соседа. При этом у двух закрашенных клеток не может быть общего соседа, и каждая отмеченная клетка является соседом некоторой закрашенной. Следовательно, можно установить взаимно однозначное соответствие между закрашенными клетками и парами отмеченных. Следовательно, количество окрашенных клеток вдвое меньше количества отмеченных клеток, то есть равно (4× 99 + 4× 95 + ... + 4× 5 + 4× 1) : 2 = 2550.

Второй способ. (Е.Ф. Каланчина, р.п. Малиновое озеро, Алтайский край) Докажем вначале, что на границе квадрата закрашено 198 клеток, причем ровно две из них – угловые.

Рассмотрим диагональ квадрата, состоящую из 2k + 1 клетки (будем называть ее основной) и две соседние с ней диагонали – из 2k и 2k + 2 клеток соответственно. Каждая клетка основной диагонали имеет ровно одного закрашенного соседа, лежащего на какой-то из соседних диагоналей. При этом каждая клетка диагонали длины 2k является соседней сразу для двух клеток основной диагонали, и каждая клетка диагонали длины 2k + 2, кроме двух крайних, также является соседней для двух клеток основной диагонали. Но количество клеток основной диагонали равно 2k + 1, то есть нечетно, поэтому среди двух крайних клеток диагонали длины 2k + 2 ровно одна закрашена.

Поскольку каждая клетка на границе квадрата является концом ровно одной диагонали четной длины, то ровно половина клеток на границе квадрата закрашена. Поскольку всего на границе квадрата 100´ 100 лежит 396 клеток, то закрашено 198 клеток, среди которых две угловые.

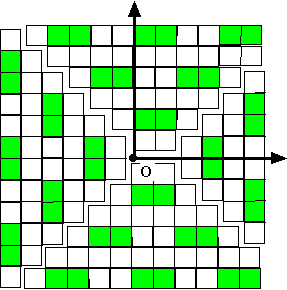
Теперь подсчитаем, сколько соседей у этих закрашенных клеток. У двух угловых клеток – по два соседа, у оставшихся 196 клеток – по три, итого: 2× 2 + 3× 196 = 592 клетки. Оставшиеся 100² – 592 = 9408 клеток квадрата имеют закрашенных соседей внутри квадрата, причем каждая закрашенная клетка внутри квадрата является соседом ровно для четырех их этих 9408 клеток. Поэтому количество закрашенных клеток внутри квадрата равно 9408 : 4 = 2352. Таким образом, общее количество закрашенных клеток равно 2352 + 592 = 2550.

(В.В. Путилов, О.Н. Чичагова, г. Пермь) Доклеим к закрашенным клеткам на границе квадрата извне дополнительные клетки, так чтобы каждая закрашенная клетка была окружена клетками со всех сторон. Тогда количество закрашенных клеток составит ровно четверть от общего количества клеток. Поскольку к каждой из угловых клеток было доклеено по две клетки, а к остальным 196 закрашенным клеткам границы – по одной, то общее количество клеток стало равным 100² + 2× 2 + 196 = 10200, и следовательно, количество закрашенных клеток равно 10200 : 4 = 2550.

II. Найдите ошибки.

5. [Из книги И.М. Яглома «Принцип относительности Галилея и неевклидова геометрия»] В 30-х годах XIX столетия Лобачевский, Бойяи и Гаусс установили, что Пятый постулат Евклида не выводится из остальных. Однако многие математики – их предшественники предпринимали различные попытки осуществить такой вывод.

Ф. Лежандр (1752 – 1833) – автор многочисленных исследований по геометрии, в том числе учебников. Учебники его многократно исправлялись, в частности по причине содержащихся в них ошибочных «доказательств» V постулата Евклида. Вот одно из них.

В этом доказательстве Лежандр опирается на две ранее доказанные теоремы. Одна из них состоит в том, что V постулат вытекает из того факта, что сумма углов любого треугольника равна 180° . Эта теорема была ранее безупречно доказана самим Лежандром. Вторая теорема (доказанная ранее Саккери, Ламбертом и другими) гласит, что сумма углов любого треугольника не превосходит 180° . Исходя из первой теоремы, мы видим, что для доказательства V постулата достаточно без опоры на него же доказать, что сумма углов любого треугольника равна 180° .

Лежандр приводит такое рассуждение «от противного». Пусть существует треугольник ABC такой, что сумма его углов равна: S(ABC) = 180° – d , где d > 0. Пусть A – наименьший (а значит, острый) угол этого треугольника. Достроим треугольник ABC до параллелограмма ABDC. Проведем через точку D прямую, пересекающую лучи AB и AC в точках K и L соответственно. Подсчитаем сумму углов в треугольнике AKL так: просуммируем углы в треугольниках ABC, BCD, BDK и CDL, а затем вычтем три раза по 180° , ибо углы при вершинах B, D и C в сумме составляют развернутые.

Получим: S(AKL) = 2S(ABC) + S(BDK) + S(CDL) – 540° = S(BDK) + S(CDL) – 180° – 2d . Далее, в силу второй указанной теоремы, заменим S(BDK) + S(CDL) на выражение 2× 180° , которое не меньше этой суммы. Получим, что S(AKL) £ 180° – 2d .

Найдите ошибку в приведенном доказательстве.

Решение. Выделенная фраза – первая и основная в этом «доказательстве», содержащая ошибку. Предыдущее построение (достраивание треугольника до параллелограмма) вполне осуществимо без применения параллельности. Например, можно продлить медиану AM треугольника ABC на ее длину за точку M. Тогда треугольники ABC и DCB будут равны, и у них будет одинаковая сумма углов. Никаких других свойств параллелограмма в дальнейших рассуждениях не используется. Однако треугольник AKL построить не всегда удастся. Может оказаться, что, пытаясь провести такую прямую, то есть, соединяя точку D со всеми точками X луча AB (лежащими вне отрезка AB), мы получим, что луч XD никогда не пересекает луч AC. Так и будет происходить в геометрии Лобачевского.

Действительно, рассмотрим прямую l и точку A вне неё. В геометрии Лобачевского через точку A проходит бесконечное множество прямых, среди которых две прямые, m₁ и m₂ являются (и называются) параллельными к l (а также граничными с l), а все, лежащие между m₁ и m₂ также не пересекаются с l (они называются расходящимися с l). Сама прямая l называется заградительной для прямых m₁ и m₂. Если m₁ и m₂ – это AB и AC, то, как только точка D попадёт в другую полуплоскость относительно прямой l (а это при многократном повторении указанного рассуждения рано или поздно произойдёт), дальнейшее построение станет невозможным.

6. [Фольклор] Известно, что числа p и q являются корнями квадратного уравнения 5x² + bx + 10 = 0. Найдите корни уравнения 10x² + bx + 5 = 0.

Первый способ. Заметим, что дискриминанты указанных уравнений одинаковы: D = b² – 200, поэтому, независимо от значения b, если первое уравнение имеет корни, то и второе также имеет корни.

Пусть, для определенности, p ³ q, тогда ; . Пусть m и n –

корни второго уравнения, причем m ³ n, тогда и .

Следовательно, m = 0,5р; n = 0,5q.

Второй способ. Из условия следует, что выполняется числовое равенство: 5p² + bp + 10 = 0, где p ¹ 0. Разделив его почленно на p², получим: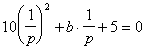 Û , то есть, число является корнем второго уравнения. Другой корень второго уравнения находим по теореме Виета: .

Таким образом, корнями второго уравнения являются числа и .

Решение. Различные ответы получились потому, что в первом способе решения ответ выражен через числа p и q, а во втором способе – только через p. Вместе с тем данные числа p и q связаны между собой. Действительно, если они являются корнями данного уравнения, то по теореме Виета pq = 2. Поэтому, если подставить, например, в выражение n = 0,5q, полученное в первом способе решения, то несложно убедиться, что ответы совпадут.

7. В квадрате АВСD со стороной 1 на сторонах АВ, ВС, СD и DA отмечены точки М, N, K и L соответственно так, что АМ + AL + CN + CK = 2. Докажите, что прямые MK и NL перпендикулярны.

Эта задача допускает очень много различных способов решения. Приведем шесть основных способов и их возможные вариации. Некоторые из способов решения требуют отдельного рассмотрения случая, когда одна из прямых MK или NL параллельна стороне квадрата. Тогда другая прямая также параллельна стороне квадрата и доказательство этого простого факта мы опускаем.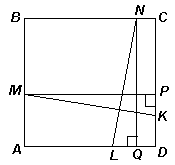

Первый способ («равенство треугольников»). Проведем отрезки MP и NQ, параллельные сторонам квадрата (см. рис. 3а). Тогда KP = |AM – DK|; LQ = |BN – AL|. Преобразуем равенство, данное в условии задачи: АМ + AL = (1 – CN) + (1 – CK). Учитывая, что квадрат – единичный, получим, что АМ + AL = BN + DK Û AM – DK = BN – AL. Таким образом, KP = LQ, тогда прямоугольные треугольники PMK и QNL равны (по двум катетам), следовательно, Ð PMK = Ð QNL. Кроме того, МР^ NQ, поэтому MK^ NL.

Отметим, что из равенства треугольников PMK и QNL следует также, что MK = NL.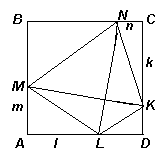

Второй способ («теорема Пифагора», О.В. Кривошеин, с. Харламово, Омская обл.). Введем обозначения: АМ = m; AL = l; CN= n; CK = k и рассмотрим четырехугольник MNKL (см. рис. 3б). Из прямоугольных треугольников МАL, NBM, KCN и LDK получим, что ML² = m² + l²; NM² = (1 – m)² + (1 – n)²; KN² = n² + k²; LK² = (1 – l)² + (1 – k)². Тогда NM² + LK² = (1 – m)² + (1 – n)² + (1 – l)² + (1 – k)² = 4 – 2(m + n + l + k) + m² + n² + l² + k² = ML² + KN², поскольку m + n + l + k = 2.

Таким образом, в четырехугольнике MNKL равны суммы квадратов противолежащих сторон. Это условие является необходимым и достаточным для того, чтобы диагонали MK и NL этого четырехугольника были перпендикулярны (см., например, Я.П. Понарин. Элементарная геометрия: В 2 т. – Т. 1: Планиметрия, преобразования в плоскости. – М.: МЦНМО, 2004, стр. 82).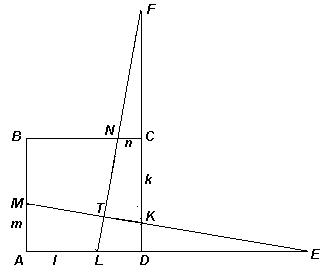

Третий способ («подобие треугольников», И.А. Акимова, г. Москва). Пусть прямые MK и NL пересекаются в точке Т. Продолжим отрезки MK и NL до пересечения с продолжениями сторон квадрата. Без ограничения общности можно считать, что прямая MK пересекла прямую AD в точке Е, а прямая NL пересекла прямую CD в точке F (см. рис. 3в). Введем обозначения: АМ = m; AL = l; CN= n; CK = k и рассмотрим две пары подобных треугольников.

1) D FCN подобен D FDL (по двум углам). Следовательно, , то есть Û .

2) D EDK подобен D EAM (по двум углам). Следовательно, , то есть Û .

Так как m + n + l + k = 2, то 1 – n – l = k + m – 1. Тогда . Следовательно, прямоугольные треугольники FCN и EDK также подобны. Поэтому Ð FNC = Ð EKD = a . Тогда в четырехугольнике CNTK: Ð CKT = a ; Ð CNT = 180° – a ; Ð NCK = 90° . Значит Ð NTK – прямой, что и требовалось доказать.

Вариациями второго и третьего способов решения являются использование площадей или теоремы косинусов.

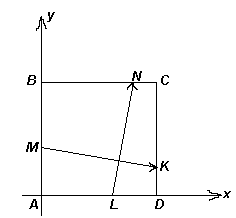
Четвертый способ («координатный»). Выберем декартову систему координат так, чтобы начало координат совпало с точкой А, а оси координат – с прямыми AD и АВ (см. рис. 3г). Тогда М(0; m); L(l; 0); N(n; 1); K(1; k). По условию АМ + AL + CN + CK = 2, следовательно, m + l + (1 – n) + (1 – k) = 2 Û m + l = n + k.

Рассмотрим векторы и . Так как , то . Следовательно, прямые MK и NL перпендикулярны.

Еще один способ решения – вместо того, чтобы вводить векторы, можно вычислить угловые коэффициенты прямых MK и NL, и, используя полученное равенство m + l = n + k, доказать, что произведение этих коэффициентов равно –1.

Можно также наоборот, не вводить систему координат, а задать векторный базис на плоскости, например, и , разложить по этому базису векторы и , и доказать, что = 0, непосредственно используя условие задачи.

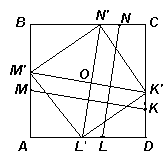
Пятый способ («параллельный перенос и центральная симметрия»). Пусть О – центр данного квадрата, тогда перенесем параллельно отрезки MK и NL так, чтобы их образы M’K’ и N’L’ проходили через точку О (см. рис. 3д). Из свойств параллельного переноса (или свойств параллелограмма) следует, что MM’ =- KK’ и LL’ =- NN’, тогда АМ’ + AL’ + CN’ + CK’ = АМ + AL + CN + CK = 2. Кроме того, АМ’ = CK’ и AL’ = CN’, так как эти отрезки попарно симметричны относительно точки О. Следовательно, АМ’ + AL’ = CN’ + CK’ = 1. Учитывая, что сторона квадрата равна 1, получим, что точки М’, L’, K’ и N’ делят стороны данного квадрата в одном и том же отношении, поэтому четырехугольник М’L’K’N’ – ромб, его диагонали M’K’ и N’L’ перпендикулярны, а значит перпендикулярны и прямые MK и NL.

Можно также доказать, что М’L’K’N’ – квадрат, откуда будет следовать, что MK = NL. Вариациями этого способа решения являются параллельный перенос отрезков MK и NL в вершины квадрата или использование поворота на 90° вокруг центра квадрата.

Шестой способ («поворот», В.В. Путилов, О.Н. Чичагова, г. Пермь). Повернем данный квадрат на 90° вокруг вершины А. Образами вершин В и С при этом повороте служат точки B’ и С’, а образами точек М и K – точки М’ и K’ соответственно (см. рис. 3е). Так как AM’ = AM и С’K’ = CK, то из условия задачи следует, что АМ’ + AL + CN + C’K’ = 2. Кроме того, так как данный квадрат – единичный, то BK’ + BN + CN + C’K’ = CC’ = 2. Следовательно, M’L = АМ’ + AL = BK’ + BN = K’N. Учитывая, что M’L || K’N получим, что четырехугольник M’K’NL – параллелограмм. Тогда M’K’ || NL, поэтому MK ^ NL.

8. Докажите, что если a + b + c = 1, то a² + b² + c² ³ .

Первый способ. Используем неравенство между средним квадратичным и средним арифметическим для трех чисел: (|x| ³ x для любого x). Тогда .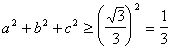

Второй способ. Сделаем замену переменных: x = a – , y = b – , z = c – , тогда x + y + z = 0. Следовательно, a² + b² + c² = + + = x² + y² + z² + + = x² + y² + z² + ³ .

Приведенный способ по сути является упрощенной реализацией метода Штурма.

Третий способ. Рассмотрим три верных неравенства: a² + b² ³ 2ab; b² + c² ³ 2bc; a² + c² ³ 2ac. Сложив их почленно, получим, что 2a² + 2b² + 2c² ³ 2ab + 2bc + 2ac. Прибавим к обеим частям полученного неравенства выражение a² + b² + c², тогда 3(a² + b² + c²) ³ (а + b + c)², то есть, a² + b² + c² ³ (а + b + c)² = .

Отметим, что вместо трех неравенств, приведенных вначале, можно было использовать известное неравенство a² + b² + c² ³ ab + bc + ac.

Четвертый способ (С.С. Гаджиев, с. Ахты, Дагестан). Пусть a² + b² + c² = S. Запишем верное неравенство: Û . Подставив в полученное неравенство a² + b² + c² = S и a + b + с = 1, получим, что Û S ³ , что и требовалось.

Пятый способ. Так как c = 1 – (a + b), то a² + b² + c² – = 2a² + 2b² + – 2a – 2b + 2ab. Полученное выражение можно рассматривать как квадратичную функцию с переменной а: f(a) = 2a² + 2(b – 1)a + (2b² – 2b + ). При каждом значении b ее графиком является парабола, «ветви» которой направлены вверх. Упрощенный дискриминант этого трехчлена D’ = (b – 1)² – 2(2b² – 2b + ) = –3b² + 2b – = –(3b – 1)² £ 0 при любом значении b, поэтому график f(a) распложен в верхней полуплоскости, то есть f(a) ³ 0. Тогда a² + b² + c² – ³ 0 Û a² + b² + c² ³ .

Шестой способ. Рассмотрим функцию f(x) = x², график которой расположен выпуклостью вниз. Для таких функций выполняется неравенство Йенсена, которое применяется, в данном случае, для трех чисел: . Таким образом, , то есть a² + b² + c² ³ .

Седьмой способ. Используем неравенство Коши - Буняковского: . Пусть x₁ = a; x₂ = b; x₃ = c; y₁ = y₂ = y₃ = 1, тогда a + b + c £ 3(a² + b² + c²). Следовательно, a² + b² + c² ³ .

Восьмой способ (Т.В. Соколова, г. Москва). Рассмотрим три вектора: , и в декартовой системе координат. Тогда и . Поскольку модуль суммы векторов не превосходит суммы их модулей, то . Следовательно, a² + b² + c² ³ .

Девятый способ. Заменим данные переменные на x, y и z. Уравнение x + y + z = 1 задает плоскость в трехмерной декартовой системе координат. Найдем расстояние d до этой плоскости от начала координат. Если плоскость a задана уравнением Ax + By + Cz + D = 0, а М(x₀; y₀; z₀), то ½ M; a ½ =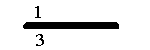 . Следовательно, d = .

Расстояние от начала координат до любой точки рассматриваемой плоскости не меньше, чем d, поэтому , то есть x² + y² + z² ³ .

Copyright ©2006 МЦНМО