VII Заочный конкурс учителей по математике

VII Заочный конкурс учителей по математике.

I. Решите задачи.

№1. Четыре велосипедиста стартовали одновременно и приехали на финиш через равные промежутки времени. Скорости самого быстрого и самого медленного из велосипедистов равны v1 и v4. Найдите скорости второго и третьего велосипедистов.

№2. Фигура “пулеметчик” – это ладья, бьющая только в одном направлении (в одну сторону). Какое наибольшее количество “пулеметчиков” можно поставить на шахматную доску так, чтобы они не били друг друга?

№3. Ребро куба АВСDA1B1C1D1 равно 1. Прямая m проходит через точку Е – середину ребра C1D1, и пересекает прямые AD1 и А1В (последнюю – в точке F). Найдите EF.

№4. Решите уравнение: (x – y)2 + (ex – y)2 = 0,5.

№5. В треугольнике АВС отмечены точки касания двух вневписанных окружностей со сторонами АС и ВС – точки В1 и А1 соответственно. Докажите, что прямая, соединяющая середины отрезков АВ и А1В1 делит периметр треугольника АВС пополам.

II. Методический блок.

В предложенных текстах (№6 и №7) могут содержаться математические ошибки (как в “ответах”, так и в “решениях”). Укажите все ошибки и если “решение” не верно, то приведите верное решение.

№6. “Задача”. Каждая сторона треугольника ABC разделена на восемь равных отрезков. Сколько существует различных треугольников с вершинами в точках деления (точки A, B и C не могут быть вершинами треугольников), у которых ни одна из сторон не параллельна ни одной из сторон треугольника ABC?

“Ответ”: 120.

“Решение”. Из условия задачи следует, что мы должны выбрать по одной точке на каждой из сторон треугольника. Выберем сначала точку на стороне AB – это можно сделать шестью способами. Тогда точку на стороне BC можно выбрать пятью способами, поскольку сторона полученного треугольника не должна быть параллельна AC. Аналогично, точку на стороне AC можно выбрать четырьмя способами (не должно быть сторон, параллельных сторонам AB и BC). Таким образом, искомое количество способов равно: 6× 5× 4 = 120.

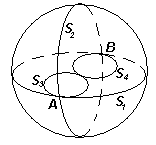
№7. “Задача”. Три окружности попарно касаются, причем точки касания различны. Верно ли, что эти окружности принадлежат либо одной плоскости, либо одной сфере?

“Ответ”: нет, не верно.

“Решение”. Рассмотрим, например, произвольную сферу и две ее большие окружности S1 и S2, лежащие в перпендикулярных плоскостях (см. рисунок). Пусть А и В – точки их пересечения. В плоскости окружности S1 рассмотрим еще две окружности S3 и S4, касающиеся окружности S1 внутренним образом в точках А и В соответственно, а друг друга – внешним образом. Тогда окружности S2, S3 и S4 попарно касаются, но не лежат в одной плоскости и не могут принадлежать одной и той же сфере.

№8. На математическом кружке была предложена задача:

Функция f(x) определена для всех действительных x и f(f(x)) = 5x + 4. Найдите f(–1).

Пять школьников получили одинаковый ответ, но привели разные решения. В них могут содержаться математические ошибки. Укажите все ошибки в каждом решении и приведите верное решение (если оно отсутствует).

“Ответ”: –1.

Решение Коли. Функция f(f(x)) возрастающая, следовательно, она обратима. Тогда , то есть . Значит, = –1.

Решение Оли. Докажем, что функция f(x) обратима. Действительно, функция f(f(x)) – обратима, так как она – возрастающая. Пусть f(x) – не обратима, тогда существуют такие различные действительные числа x1 и x2, что f(x1) = f(x2). Значит, f(f(x1)) = f(f(x2)) – противоречие.

Из доказанного утверждения и условия задачи следует, что , тогда , значит графики функций f(x) и f–1(x) пересекаются на прямой y = x, то есть = –1.

Решение Толи. Из условия задачи следует, что функция f(x) – линейная, значит, она либо возрастающая, либо убывающая, поэтому функция f(x) обратима.

Тогда , то есть , значит графики функций f(x) и f–1(x) пересекаются на прямой y = x, поэтому, = –1.

Решение Поли. Подставим в исходное равенство x = –1, тогда . Следовательно, , значит графики функций f(x) и f–1(x) пересекаются на прямой y = x, поэтому, = –1.

Решение Вали. Из условия задачи следует, что функция f(x) – линейная. Пусть f(x) = kx + b, тогда f(f(x)) = k(kx + b) + b = k2x + b(k + 1). По условию задачи f(f(x)) = 5x + 4, поэтому: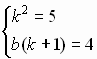 . Решая эту систему, получим: , или , . Таким образом, или . В обоих случаях = –1.

№9. В различных пособиях по математике для школьников рассматриваются, в основном, три “подхода” для решения иррациональных, логарифмических и некоторых других типов уравнений: 1) постепенный переход от уравнения к его следствиям с последующей подстановкой всех полученных корней в исходное уравнение; 2) поиск ОДЗ и проверка, что полученные корни удовлетворяют ОДЗ; 3) переход на каждом этапе к равносильным условиям.

В чем, на ваш взгляд, заключаются достоинства и недостатки каждого из “подходов”? Обоснуйте свою точку зрения, приводя соответствующие примеры.