6. Арбуз весил 10 кг и содержал 99% воды. После того, как он немного подсох, содержание воды в нём уменьшилось до 98%. Сколько он весит теперь?
7. Имеется автомат с двумя кнопками и экраном. Сначала на экране горит число 0. При нажатии на одну кнопку число на экране увеличивается в 3 раза. При нажатии на вторую кнопку число увеличивается в 3 раза и прибавляется 1. Можно ли получить на экране число 85?
8. Докажите, что
1-1/2+1/3-1/4+...+1/199-1/200=1/101+1/102+...+1/200.
9. Какое максимальное число ладей можно разместить на шахматной доске 8x8, чтобы каждая из них стояла под ударом не более чем одной из остальных?
10. Нарисуйте два несамопересекающихся пятиугольника так, чтобы у них были одни и те же вершины, но не было ни одной общей стороны.
11. Может ли сумма 1+2+3+...+k оканчиваться на 7 при каком-либо k?
12. Имеется 4 куска мягкой проволоки. Каждый кусок имеет длину 1. Как, не разрезая проволоки, сделать каркас прямоугольного параллелепипеда 0,5x0,3x0,2?
13. На листе бумаги записали подряд все числа от 1 до 1000. Сколько цифр 3 при этом было использовано?
14. Петя и Вася по очереди соединяют соседние (находящиеся на расстоянии 1) вершины бесконечного листа клетчатой бумаги (Вася - красным цветом, Петя - синим). Первым ходит Вася. Докажите, что Петя может помешать Васе образовать красную замкнутую линию.
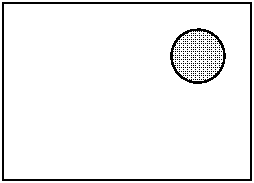
15. На прямоугольном торте лежит круглая шоколадка. Как одним прямолинейным разрезом разделить и торт, и шоколадку поровну (на две части одинаковой площади)?

16. На плоскости нарисован чёрный квадрат. Имеется семь квадратных плиток того же размера. Нужно положить их на плоскость так, чтобы они не перекрывались и чтобы каждая плитка покрывала часть чёрного квадрата (хотя бы одну точку внутри него). Как это сделать?
17. Существует ли целое положительное число, делящееся на 2001, десятичная запись которого начинается на 123456789?
18. Можно ли увезти из каменоломни 50 камней, веса которых 370 кг, 372 кг, 374 кг, ..., 468 кг (каждый на 2 кг тяжелее предыдущего) на 7 машинах, загружая в каждую не более 3000 кг?
19. На электронных часах высвечиваются часы, минуты и секунды (от 00:00:00 до 23:59:59). Сколько времени в течение суток хотя бы на одном месте горит цифра 2?
20. У числа 71000 подсчитали сумму цифр, у полученного числа вновь подсчитали сумму цифр и так далее, до тех пор пока не получили однозначное число. Что это за число?
21. Шахматная доска 8x8 выложена 32 доминошками 1x2. Докажите, что какие-то две доминошки образуют квадрат 2x2 (примыкая длинными боками).
22. Каждую сторону прямоугольника увеличили на 3 см; в результате его площадь увеличилась на 39 квадратных сантиметров. Потом каждую сторону прямоугольника увеличили ещё на 3 см. На сколько при этом увеличилась его площадь?
23. В таблице 10x10 по порядку расставили числа от 0 до 99 (в первой строке - от 0 до 9, во второй строке - от 10 до 19 и т.д). Затем перед каждым из чисел поставили знак "+" или "-"; при этом в каждой строке и каждом столбце оказалось по пять знаков "+" и пять знаков "-". Чему может быть равна сумма всех чисел таблицы с учетом расставленных знаков?
24. Человек приехал на станцию на час раньше обычного и не стал ждать посланную за ним машину, а пошёл ей навстречу, встретил, сел и приехал на 20 минут раньше обычного. Сколько минут он шёл пешком? (Скорости человека и машины постоянны.)
25. Саша и Витя выписывают шестизначное число, записывая по очереди цифры слева направо (сначала старшую цифру, затем следующую и т.д.); начинает Саша. Как должен действовать Витя, чтобы полученное число делилось на 7?