6. Может ли квадрат одного целого числа быть вдвое больше квадрата другого целого числа? Если может, то приведите пример, а если нет - то докажите.
7. По шоссе в данном направлении с постоянной скоростью через равные интервалы идут без остановок автобусы. Один раз человек прошёл 4 км и его обогнали 4 автобуса, другой раз он прошёл 7 км и его обогнали 8 автобусов. В третий раз он прошёл (с той же скоростью, что и в первые два раза) 17 км. Сколько автобусов при этом его обогнали? Укажите все варианты.
8. Игра домино состоит из 28 костей с парами цифр от 0 до 6 (кости 0:0, 0:1, 0:2, ..., 0:6, 1:1, 1:2, ..., 1:6, 2:2, ..., 2:6, 3:3, ..., 5:5, 5:6, 6:6). Кости выложены в цепочку, причём одинаковые цифры прикладываются друг к другу. На одном конце цепочки цифра 5. Какая цифра на другом конце? Почему?
9. Из доски 8x8 по клеточкам вырезали 12 прямоугольников 1x2. Обязательно ли из оставшейся части можно "по клеточкам" вырезать прямоугольник 1x3?
10. Найдите все пары натуральных чисел x и y, для которых x+y=xy.
11. В шахматном турнире участвовали 2 семиклассника и несколько восьмиклассников. Оба семиклассника набрали вместе ровно 16 очков, а все восьмиклассники набрали очков поровну. Сколько восьмиклассников участвовало в турнире? (Каждый играл с каждым по разу, за выигрыш давалось 2 очка, за ничью - 1 очко, за проигрыш - 0 очков.)
12. Из 11 шаров 2 радиоактивны. Про любой набор шаров за одну проверку можно узнать, имеется ли в нём хотя бы один радиоактивный шар (но нельзя узнать, сколько их). Можно ли за 7 проверок найти оба радиоактивных шара?
13. За завтраком каждый выпил по чашке кофе с молоком, причём Дима выпил пятую часть всего выпитого молока и восьмую часть всего выпитого кофе. Сколько человек могло участвовать в завтраке? (Все чашки одинаковы, но пропорции молока и кофе в них могут быть разными.)
14. Нужно сварить 4 яйца вкрутую и 2 яйца всмятку. Яйца вкрутую варятся 4 минуты, яйца всмятку - 2 минуты. Имеется кастрюлька, вмещающая 4 яйца. Можно ли сделать требуемое за 5 минут? A за 4 минуты? Обоснуйте свой ответ.
15. Можно ли замостить плоскость квадратами, среди которых не более двух одинаковых?
16. Гриша пошёл с папой в тир. Уговор был такой: Гриша делает 5 выстрелов, а за каждое попадание в цель делает ещё два дополнительных выстрела. Всего было 17 выстрелов. Сколько раз Гриша промахнулся?
17. Процент учеников класса, получивших двойку за контрольную работу по математике, составляет от 26,5% до 26,7%. Каково наименьшее число учащихся в этом классе и сколько из них получили двойку?
18. Прямоугольник размером 2m x 2n выложен костями домино размера 1x2. Докажите, что можно так выложить второй слой костями домино, что никакая кость второго слоя не будет лежать в точности над какой-то костью первого слоя.
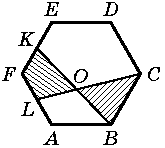
19. На свой день рождения Саша испёк торт, имеющий форму правильного шестиугольника ABCDEF (см. рис.). Потом Саша отметил точки K и L, являющиеся серединами сторон EF и FA. Треугольный кусок BOC он дал Вите, а четырёхугольный кусок KOLF - Мите. Кому из мальчиков достался больший кусок?

20. У Васи есть пластмассовый угольник (без делений) с углами 30 градусов, 60 градусов и 90 градусов. Ему нужно построить угол в 15 градусов. Как это сделать, не используя других инструментов?
21. Найдите сумму всех целых чисел от -2001 до 2003.
22. Несколько ящиков вместе весят 10 тонн, причём каждый из них весит не более одной тонны. Сколько трёхтонок заведомо достаточно, чтобы увезти этот груз? (Докажите, что указанного вами числа заведомо хватит, и приведите пример, показывающий, что меньшего числа трёхтонок может не хватить.)
23. Решите уравнение:
1-(2-(3-(...(1998-(1999-(2000-x)))...)))=1000.
24. Найдите все такие числа, которые при зачёркивании первой цифры уменьшаются в 57 раз.
25. Известно, что a и b - целые числа, 7a+5b=111. Может ли a+b быть чётным? Почему?