6. Нужно выбрать 15 различных целых положительных чисел, сумма которых равна 123. Укажите все варианты.
7. Три круга радиуса 1 имеют общую точку. Докажите, что центры этих кругов можно покрыть кругом радиуса 1.
8. Трое школьников решали задачи домашнего задания. В итоге каждую задачу хоть кто-то да решил, и каждый из школьников решил 11 задач. Сколько задач в задании, если трудных задач (решённых только одним из троих) оказалось на 5 больше, чем лёгких (решённых всеми)?
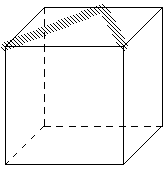
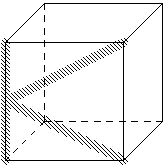
9. Внутри куба находится спаянная из проволоки штука, которая в проекции на верхнюю грань (вид сверху) даёт букву Л, а в проекции на переднюю грань (вид спереди) даёт букву К. Что даёт она в проекции на боковую грань?


10. На острове живут братья-близнецы Петя и Вася. Один из них всегда говорит правду, другой всегда лжёт. Путешественник, знающий про это, встретил одного из них. Желая узнать, говорит ли Вася правду, он спросил встреченного: "Ты .... ?". Что он спросил?
11. Может ли пятно на полу, имеющее форму равностороннего треугольника, быть целиком покрыто двумя ковриками той же формы, но меньшего размера?
12. Может ли пятно на полу, имеющее форму квадрата, быть целиком покрыто тремя ковриками той же формы, но меньшего размера?
13. Какое наибольшее число ладей можно поставить на шахматную доску 8x8, если требуется, чтобы хотя бы одна из них не била ни одной другой?
14. Коробка 3x4x5 заполнена деревянными кубиками 1x1x1 (всего 3*4*5=60 кубиков). Жук-древоточец прогрыз прямой ход из одного угла коробки в противоположный (самый дальний). Сколько кубиков он испортил?
15. Числа
a1=1, a2=1+1/1=2, a3=1+ 1/(1+1/1)=3/2, a4=1+ 1/(1+1/(1+1/1))=5/3, ...
строятся по такому правилу: каждое следующее на единицу больше обратного к предыдущему, то есть an+1=1+1/an. Расположите в порядке возрастания первые десять из них (a1, ..., a10). (Например, для первых четырёх чисел ответ был бы таким: a1<a3<a4<a2.)
16. На прямой выбраны две точки A и B на расстоянии 12. Где на прямой может находиться точка C, если известно, что расстояние AC вдвое больше расстояния BC? (Укажите все варианты.)
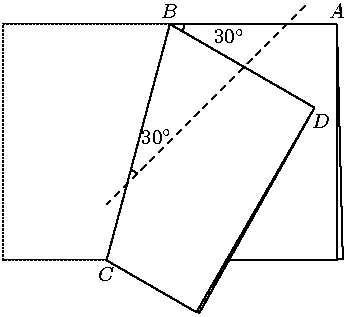
17. Вася сложил листок бумаги пополам, потом перегнул его ещё раз и отрезал ножницами по прямой. Развернув листок, он обнаружил в его центре многоугольную дырку. Найдите углы этого многоугольника.
18. Может ли шахматный конь обойти все клетки доски 5x5, побывав в каждой клетке по одному разу и вернувшись в исходную клетку?
19. Тот же вопрос, если возвращаться в исходную клетку не обязательно.
20. Из пяти одинаковых с виду монет одна фальшивая. Неизвестно, легче она остальных или тяжелее. Как это узнать, сделав не более 2 взвешиваний на чашечных весах без гирь?
21. Сколько существует различных шестигранных игральных костей с цифрами 1, ..., 6 на гранях? (Две кости считаются одинаковыми, если их можно повернуть так, чтобы числа на соответствующих гранях совпали.)
22. Целые числа x и y таковы, что 31x=17y. Докажите, что число x+y делится на 24.
23. Целое положительное число делится на 6 и имеет ровно 14 целых положительных делителей (считая 1 и само число). Что это за число? Укажите все варианты.
24. Предполагалось, что среди школьников, идущих на экскурсию, девочки будут составлять 25% от числа мальчиков. Однако вместо одной девочки пришел мальчик, в результате чего число девочек стало составлять 20% от числа мальчиков. Сколько школьников участвовало в экскурсии?
25. Квадрат целого положительного числа x начинается на 12, то есть
x2=12...
На какие две цифры может начинаться само число x? Укажите все варианты.