Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере две из предлагаемых 5 задач. Для этого он должен не позднее 24 сентября выслать полные решения задач по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить пустой незаклеенный конверт с написанным на нём своим адресом и маркой. (В этом конверте будут посланы результаты проверки и следующие задачи.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/.
Желаем успеха!
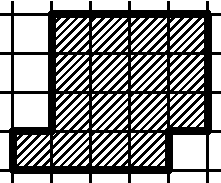
1. Разрежьте фигуру на рисунке на две равные (по форме и величине) части, проведя линию разреза по сторонам клеток.

2. Из одной точки выходят четыре луча OA, OB, OC, OD (перечисленные по часовой стрелке), которые делят плоскость на четыре угла, три из которых таковы: ∠AOB = 45°, ∠BOC = 90°, ∠COD = 105°, Найдите четвёртый угол AOD. Найдите углы AOC и BOD.
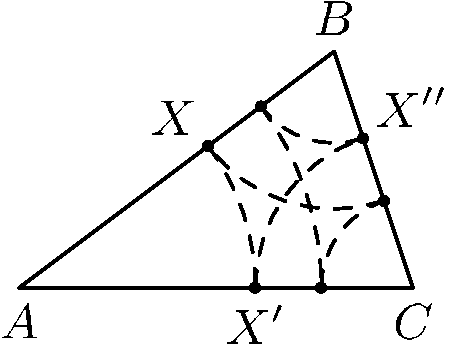
3. На стороне AB треугольника ABC взята произвольная точка X. Затем на стороне AC взята точка X', для которой AX=AX'. После этого на стороне BC взята точка X'', для которой CX'=CX'' и так далее. Докажите, что после нескольких раз мы попадём в исходную точку X.
4. На большом поле есть узкая прямая канава длиной 500 м. Турист стоит на берегу канавы на расстоянии 200 м от её конца (и 300 м от другого конца). Нарисовать часть поля, в которую он может попасть, пройдя не более 400 метров (и не переходя канавы). Из каких линий состоит граница этой части?
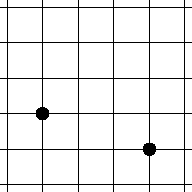
5. На клетчатой бумаге отмечены две точки. Добавьте к ним ещё две таким образом, чтобы четыре получившиеся точки были вершинами квадрата. Укажите все возможные варианты. (Клетчатая бумага продолжается неограниченно во все стороны.)