Решения (не только ответы!) нужно до 17 ноября выслать простым (не заказным) письмом по адресу:
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс,
На письме должен быть указан обратный адрес, включая имя и фамилию. Стоимость письма зависит от его веса: 11,80 рублей (для писем до 20 г) плюс 1,25 рублей за каждые последующие полные или неполные 20 г.
В письмо следует вложить два пустых незаклеенных конверта с написанным на нём своим адресом и маркой. (В одном конверте будут посланы результаты проверки и приглашение на разбор задач и награждение; другой может быть использован для отправки Вам заданий следующего конкурса.) В это же письмо просим вложить заполненную карточку участника заочного конкурса. На каждом листе работы просим указывать фамилию, имя, номер школы и класс.
Пожалуйста, перед отправкой письма проверьте еще раз, правильно ли указана вся необходимая информация, перечтя внимательно наши инструкции - это облегчит нашу работу и уменьшит вероятность ошибок.
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), или (это надёжнее) по электронной почте: zmk@mccme.ru (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/; в начале декабря там будет информация о том, где и когда будет разбор и награждение, а после разбора и награждения помещён список победителей конкурса.
* * *
6. Шесть машин едут по дороге из города А в город Б. В данный момент они находятся в разных точках дороги, но известно, что суммарное расстояние, которое проехали (считая от А) все машины - 75 километров, а до Б осталось им ехать (тоже в сумме) 45 километров. Какова длина дороги из А в Б?
7. В Париже в течение долгого времени хранился эталон метра (пока метр не стали определять через длину световых волн, а потом через скорость света и единицы времени), однако эталона градуса там никогда не было. Как вы думаете, почему?
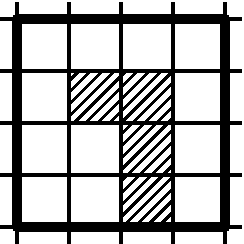
8. Разрежьте квадрат на рисунке на четыре равные (по форме и величине) части, проведя линию разреза по сторонам клеток; в каждую часть должно попасть по одной заштрихованной клетке.

9. Даны две (различные) точки A и B. Нарисуйте, где может находиться точка C, если известно, что треугольник ABC равнобедренный (имеет две равные стороны). (Будьте внимательны и не пропустите каких-либо вариантов расположения!)
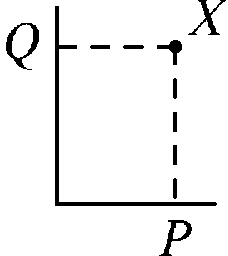
10. Дан прямой угол. Из произвольной точки X внутри этого угла опускают перпендикуляры XP и XQ на стороны этого угла. Где находятся точки X, для которых расстояние между точками P и Q меньше 1?
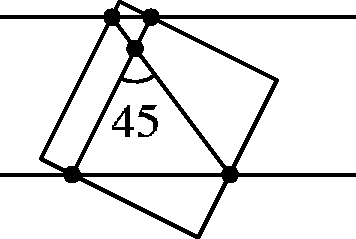
11. Два угла квадрата со стороной a выступают за пределы полосы ширины a с параллельными краями. Стороны квадрата пересекают края полосы в четырёх точках. Докажите, что диагонали четырёхугольника, вершинами которого являются эти точки, пересекаются под углом в 45 градусов.
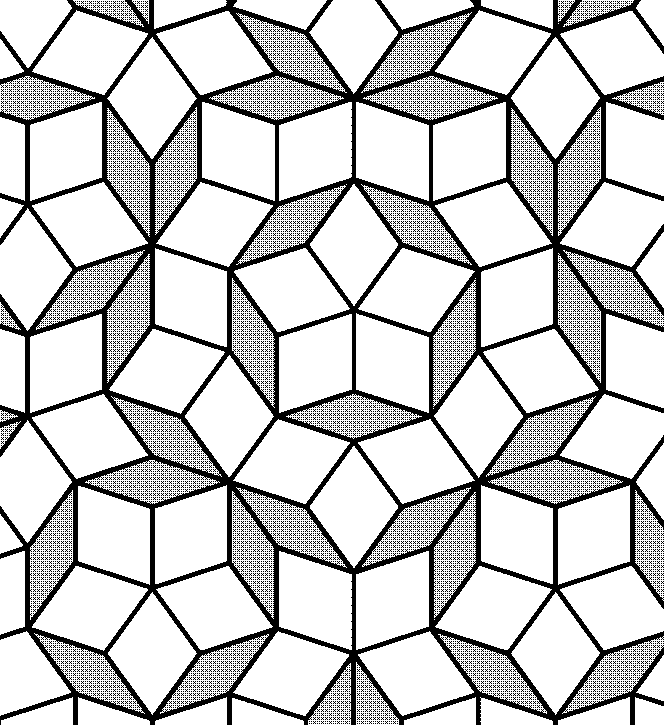
12. Замощение Пенроуза (названное в честь Роджера Пенроуза, предложившего его в 1970-е годы) покрывает плоскость ромбами двух типов, как показано на рисунке. Каковы углы этих ромбов?
13. Раскрасьте вершины клеток на клетчатой бумаге в пять цветов таким образом, чтобы узлы каждого цвета сами образовывали квадратную сетку, причём все пять сеток имели одинаковый размер клетки. (Непокрашенных вершин не должно быть.)
14. Дан треугольник ABC и точка O внутри него. Мы хотим найти отрезок с серединой в точке O, концы которого лежат на границе треугольника ABC. Какое максимальное количество решений может иметь эта задача?
15. Каждая из сторон четырёхугольника ABCD поделена на три равные части, и точки деления соединены отрезками (см. рисунок). Покажите, что каждый из этих отрезков делится другими также на три равные части.
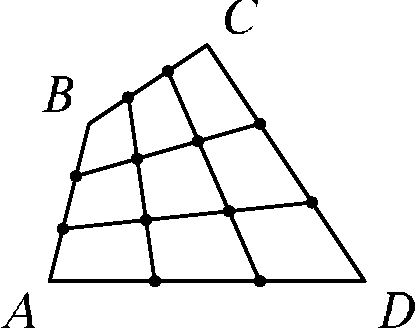
16. Несколько окружностей имеют общую точку и касаются друг друга в этой точке. Докажите, что можно провести отрезок, который пересекает все эти окружности в разных точках, но под одним и тем же углом (см. рисунок).

17. Биссектрисы всех четырёх углов выпуклого четырёхугольника со сторонами a, b, c и d (перечисленными в порядке обхода по часовой стрелке) пересекаются в одной точке. Докажите, что a+c=b+d.
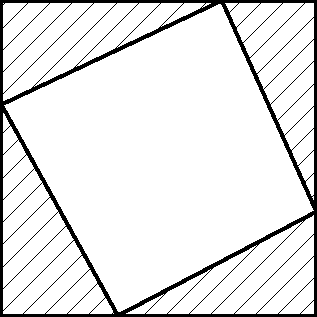
18. Четырёхугольник вписан в квадрат (на каждой стороне квадрата лежит по вершине четырёхугольника). Оказалось, что четыре получившихся при этом треугольника имеют равные площади. Докажите, что эти треугольники равны.
19. Рассказывают, что на каком-то тесте по математике была дана задача: Гипотенуза прямоугольного треугольника равна 10, а опущенная на неё высота равна 6. Чему равна площадь треугольника? Легенда гласит, что хорошие ученики получили за этот пункт теста мало очков, а плохие - много. Как вы думаете, почему такое могло случиться?
20. Найдите отношение сторон прямоугольника, разрезанного на квадраты, как показано на рисунке.

21. Могут ли три высоты треугольника иметь длины 1/2, 1/3 и 1/6?
22. Докажите, что площадь выпуклого четырёхугольника со сторонами a, b, c, d (перечислены по часовой стрелке) не превосходит (ac+bd)/2, и равенство возможно только для четырёхугольников, вписанных в окружность.
23. Имеются квадратные плитки двух разных размеров - большие и маленькие. Замостите ими плоскость без пропусков и перекрытий, причём так, чтобы у каждой большой плитки было четыре маленьких соседа, а у каждой маленькой плитки - четыре больших.
24. Покажите, что плоскость (бесконечную во все стороны) можно замостить без пробелов и перекрытий квадратами, причём так, что среди квадратов не будет двух равных.
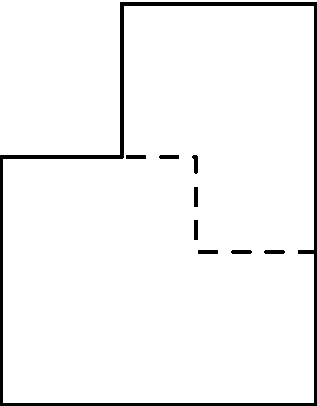
25. Шестиугольник с прямыми углами разрезан на два шестиугольника той же формы, но меньшего размера (с пропорционально уменьшенными сторонами). Найдите стороны исходного шестиугольника (приняв наибольшую из них за единицу).