6. Напишите десять чисел (не обязательно целых) так, чтобы каждое следующее число было не меньше предыдущего, чтобы сумма их квадратов равнялась 2 и чтобы третье по счету число было как можно больше.
7. Монету обкатывают вокруг такой же неподвижной монеты. Сколько оборотов вокруг своей оси она сделает к моменту возвращения в исходную точку?
8. Четыре деревни расположены в вершинах квадрата со стороной 10км. Можно ли соединить их между собой дорогами общей длиной менее 28км?
9. Несколько ящиков вместе весят 10 тонн, причем каждый из них весит не более одной тонны. Сколько трехтонок заведомо достаточно, чтобы увезти этот груз? (Докажите, что указанного вами числа заведомо хватит, и приведите пример, показывающий, что меньшего числа трёхтонок может не хватить.)
10. В клетках шахматной доски 100 на 100 написаны целые числа, причем так, что стоящие в соседних клетках числа различаются не более чем на 10. (Соседними считаются клетки, имеющие общую сторону.) Докажите, что на доске имеются по крайней мере 3 одинаковых числа.
11. Кузнечик прыгает вперёд и назад по прямой большими и маленькими прыжками. Большой прыжок составляет 12см, малый - 7см. Как ему попасть из точки O в точку A, находящуюся от точки O на расстоянии 3см?
12. Сколько цифр в числе 2100 (произведение 100 двоек)?
13. Какую цифру a нужно приписать к числу 97 справа и слева, чтобы полученное число a97a делилось на 27?
14. Две команды соревновались в 10 видах спорта. В каждом виде за выигрыш начислялось 3 очка, за ничью - 2, за проигрыш - 1 очко. Одна из команд набрала 25 очков. Выиграла она или проиграла?
15. В погребе стоят 20 одинаковых банок варенья - 8 с клубничным, 7 с малиновым и 5 с вишнёвым. Каково наибольшее число банок можно вынести в темноте из погреба, будучи уверенным, что там осталось хотя бы 4 банки одного сорта и 3 другого?
16. Из числа 1234567891011121314...585960 (подряд записаны натуральные числа от 1 до 60) вычеркните 100 цифр так, чтобы оставшееся число было наибольшим. Докажите, что ваш вариант - наилучший.
17. На концах отрезка стоят единицы. На каждом шаге между каждыми двумя соседними числами на отрезке пишется их сумма (после первого шага будет написано 1,2,1, после второго 1,3,2,3,1 и т.д.). Найдите сумму всех чисел, стоящих на отрезке после 10 шагов.
18. Натуральное число a увеличили на 1, при этом его квадрат увеличился на 1001. Чему равно a?
19. На клетках шахматной доски 8x8 написаны числа. Разрешается проделывать (в любом порядке и сколько угодно раз) две операции: (1) менять местами числа в соседних клетках; (2) заменять два соседних числа их полусуммой. Докажите, что все числа можно сделать равными.
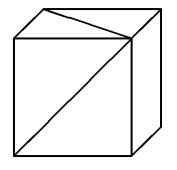
20. Из одной вершины куба проведены две диагонали его граней (см. рисунок). Какой угол они образуют?

21. Было два положительных числа. Одно из них увеличили на 1 процент, второе - на 4 процента. Могла ли их сумма увеличиться на 3 процента? (Если да, приведите пример, если нет - объясните, почему.)
22. Является ли число 1+1/2+1/3+1/4+...+1/100 целым?
23. Какое наименьшее число распилов необходимо, чтобы распилить куб со стороной 3см на 27 кубиков со стороной 1см? (Распил производится по плоскости; между распилами части разрешается перекладывать и пилить сразу несколько частей.)
24. Из чисел 1,2,3,...,200 выбрали 101 число. Докажите, что среди выбранных чисел есть пара таких, что одно из них делится на другое.
25. Известно, что a и b - целые числа, 7a+5b=111. Может ли a+b быть четным? Почему?