6. Можно ли выписать числа 1, 2, 3, 4, 5, 6, 7, 8, 9 по кругу в таком порядке, чтобы сумма любых двух соседних чисел не делилась ни на 3, ни на 5, ни на 7?
7. Найдите сумму всех пятизначных чисел, составленных из цифр 1 и 2.
8. Какое наименьшее число участников может быть в математическом кружке, если известно, что девочек в нём меньше 50%, но больше 40%?
9. Процессия движется из пункта А в пункт Б со скоростью 5 км/ч. Каждые полчаса участники процессии посылают гонцов в пункт Б. Гонцы бегут со скоростью 20 км/ч. С какими интервалами прибывают гонцы в Б?
10. Какие значения может принимать средний по величине (не наибольший и не наименьший) угол треугольника?
11. Решите уравнение
99-98(99-98(99-98(99-98(99-98(99-98x))))) = x.
12. Решите неравенство
99-98(99-98(99-98(99-98(99-98(99-98x))))) > x.
13. Можно ли пересечь куб плоскостью так, чтобы в сечении получился семиугольник?
14. Нарисуйте на клетчатой бумаге все точки, расстояние от которых до ближайшей горизонтальной границы клетки больше, чем до ближайшей вертикальной.
15. Существуют ли целые положительные числа, которые при зачёркивании первой цифры уменьшаются ровно в 57 раз?
16. В каком отношении нужно смешать трёх- и тридцатипроцентный растворы, чтобы получить двенадцатипроцентный раствор?
17. Можно ли разрезать квадрат на несколько тупоугольных треугольников?
18. Плоскость раскрашена в два цвета (есть точки и того, и другого цвета). Возможно ли, чтобы любые две точки, находящиеся друг от друга на расстоянии 1 см, были окрашены в один цвет?
19. Плоскость раскрашена в два цвета (есть точки и того, и другого цвета). Возможно ли, чтобы любые две точки, находящиеся друг от друга на расстоянии 1 см, были окрашены в разные цвета?
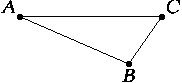
20. Сколькими способами можно приставить к треугольнику ABC на рисунке ещё один треугольник так, чтобы они не перекрывались и вместе составляли равнобедренный треугольник?

21. Можно ли так написать на шести гранях кубика числа 1, 2, 3, 4, 5, 6, чтобы числа на соседних гранях отличались не более чем на 2?
22. Верёвку сложили пополам, потом ещё раз пополам, потом снова пополам, а потом разрезали в каком-то месте. Два из получившихся кусочков имели длину 9 см и 4 см. Какова длина верёвки? Укажите все возможности. (Режут не на сгибе и сразу все нити.)
23. Куда легче попасть с одного и того же расстояния биллиардным шаром радиусом 5 см: внутрь ворот шириной 20 см (не задевая их границ) или в столбик шириной 1 см? Почему?
24. Сто разных фишек положены в ряд. Любые две фишки, стоящие через одну, разрешается поменять местами. Можно ли с помощью таких операций переставить фишки в обратном порядке?
25. Возьмём отрезок [0,1]. Отрежем от него четверть слева, потом четверть (от оставшейся части) справа, потом снова четверть (от оставшейся части) слева и так далее. Укажите точку, которая никогда не будет отрезана.