6. Петя хочет выписать 60 двузначных чисел так, чтобы среди них не было двух, дающих в сумме 100. Удастся ли ему это?
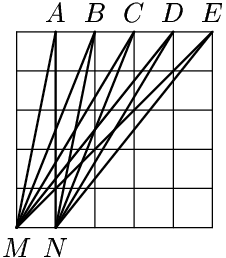
7. Найдите сумму величин углов MAN, MBN, MCN, MDN и MEN, нарисованных на клетчатой бумаге так, как показано на рисунке.

8. Целое число N разделили на 7; после запятой в частном идут цифры 42... Какой остаток даёт N при делении на 7?
9. В таблице 8x8 расставлены числа, причём известно, что сумма любых трёх чисел, стоящих подряд по горизонтали или по вертикали, равна 30. Какое максимальное количество различных чисел может быть в таблице?
10. При проверке задач 1-5 выяснилось, что каждую задачу решило нечётное число школьников, а каждый школьник решил нечётное число задач. Чётное или нечётное число школьников участвует в конкурсе?
11. Докажите, что любое пятизначное число больше произведения своих цифр.
12. Можно ли представить число 1 в виде суммы 2002 дробей, числители которых равны 1, а знаменатели - нечётные числа?
13. На территории страны, имеющей форму квадрата 1000x1000 км, находится 51 город. Докажите, что как бы ни были расположены города, их можно соединить сетью дорог длины не более 11000 км.
14. Как разрезать квадрат на 20 равных треугольников, если разрезы, параллельные сторонам квадрата, проводить запрещается?
15. Существует ли шестиугольник, у которого все углы равны, а длины сторон равны 1, 2, 3, 4, 5, 6 (не обязательно в этом порядке)?
16. Разрежьте треугольник на 4 части так, чтобы любые две из них прилегали друг к другу (имели общий отрезок границы).
17. На плоскости проведено 7 прямых, никакие две из которых не параллельны. Докажите, что найдутся две из них, угол между которыми меньше 26 градусов.
18. Можно ли внутри квадрата со стороной 1 разместить непересекающиеся круги, сумма радиусов которых больше 100?
19. Можно ли внутри квадрата со стороной 1 разместить непересекающиеся круги, сумма квадратов радиусов которых больше 100?
20. В таблице 3x3 стоят плюсы и минусы. Разрешается менять все знаки в одной строке или в одном столбце на противоположные. Можно ли за несколько шагов превратить
| + | - | - | - | - | + | |
| - | + | + | в | + | - | - |
| - | + | + | - | - | + |
21. На плоскости нарисовано несколько точек. Из каждой точки провели отрезок к ближайшей к ней точке (одинаково близких не оказалось). Могли ли некоторые из проведенных отрезков образовать замкнутую ломаную?
22. Каждая грань кубика 2x2x2 разделена на четыре квадрата 1x1; каждый квадрат окрашен в один из трёх цветов: синий, жёлтый или красный. Известно, что квадраты, имеющие общую сторону (в том числе лежащие на разных гранях), окрашены в разные цвета. Сколько при этом может быть красных квадратов?
23. Даны четыре числа; сумма любых трёх из них чётна. Докажите, что все числа чётны.
24. Можно ли из 99 одинаковых квадратных плиток составить на плоскости замкнутую цепочку (каждая следующая плитка должна иметь общую сторону с предыдущей и не налегать на неё)?
25. Отрезок [0,1] разделили на 2100 равных частей. В каком отношении точка 1/3 делит ту часть, в которую попадает?