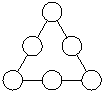
6. Разместите числа 1,2,3,4,5,6 в кружках на рисунке так, чтобы сумма трех чисел, расположенных вдоль любой стороны треугольника, была одна и та же.

7. Может ли число делиться на 12, а при делении на 8 давать остаток 6? Объясните свой ответ.
8. Среди музыкантов каждый седьмой - шахматист, а среди шахматистов каждый девятый - музыкант. Кого больше: музыкантов или шахматистов? Во сколько раз?
9. Число x - натуральное. Из неравенств 2x>70, x<100, 3x>25, x≥10, x>5 два неверных и три верных. Чему равно число x?
10. Есть ровно 7 способов заплатить A рублей, имея только трёшки и пятёрки. Чему может быть равно A? (Укажите все варианты.)
11. В клетках бесконечного листа клетчатой бумаги расположены натуральные числа, причем каждое из них равно среднему арифметическому четырёх соседних (стоящих справа, слева, сверху и снизу). Докажите, что все числа равны.
12. Часы испорчены: их стрелки движутся равномерно, но с неправильной скоростью. На сколько часов они отстают или уходят вперёд в сутки, если показывают верное время 1 раз за каждые сутки?
13. (Продолжение) Та же задача, но часы показывают верное время 3 раза за каждые сутки.
14. Улитка ползла в течение 6 минут. За ней в это время наблюдало несколько человек, каждый из них наблюдал ровно 1 минуту, и за каждую такую минуту она проползла не больше 1 метра. Ни в один момент улитка не оставалась без наблюдения. Могла ли она проползти больше 6 метров?
15. В скольких натуральных четырёхзначных числах (от 1000 до 9999) некоторая цифра встречается ровно 3 раза?
16. Нарисуйте на плоскости 5 прямых и 10 точек так, чтобы на каждой прямой лежало 4 точки, а через каждую точку проходило бы 2 прямые.
17. В строчку написаны числа от 1 до 9:
1 2 3 4 5 6 7 8 9
Нужно расставить между ними 5 знаков "+" и 3 знака "-" так, чтобы полученное выражение равнялось 21. Сколькими способами это можно сделать?
18. Перечислите все прямоугольники со сторонами длиннее 10 см, которые можно разрезать на 28 прямоугольников размера 3x5 см.
19. В кузове грузовой машины, имеющем размеры 3 на 4 метра, оставили бревно длиной 2 метра с гвоздём в середине. При движении оно свободно каталось в кузове и царапало дно. Какая часть дна кузова могла при этом поцарапаться?
20. Сумма нескольких чисел равна 1. Может ли сумма их квадратов быть меньше 0,01?
21. Пароход плывет вниз по течению реки от А до Б в течение 5 дней, а обратно (с той же скоростью) - 7 дней. Сколько дней будут плыть по течению плоты из А в Б?
22. Найдите обыкновенную дробь с наименьшим возможным знаменателем, заключенную между 2/5 и 3/7.
23. Придумайте четырёхзначное число abcd, делящееся на произведение двузначных чисел ab и cd. (Запись ab... означает число, составленное из цифр a,b,...)
24. Купец нанял работника на год за 12 рублей и кафтан. Работник ушел через 9 месяцев, получив кафтан и 8 рублей. Сколько рублей стоит кафтан?
25. Несколько брёвен распилили на поленья, сделав 57 распилов. Сколько было брёвен, если получилось 103 полена?