1. Найдите какое-нибудь целое положительное число n, при котором число 9999n (произведение 9999 и n) оканчивается на 2007 (то есть имеет вид ...2007).
2. Вася пишет на доске числа. Первое число он написал "от балды", а каждое следующее число на единицу больше суммы всех предыдущих чисел. Десятое написанное им число равно 100. Какое число Вася написал восьмым?
3. Напишите выражение, в которое входят числа 1, 3, 4, 6 (каждое ровно по одному разу - не больше и не меньше), а также знаки сложения, вычитания, умножения, деления и скобки - так, чтобы значение этого выражения было равно 24. (Примеры выражений: (1+4)x3-6, 1/3+4x6; составлять из цифр двузначные числа нельзя, использовать возведение в степень, извлечение корня и другие подобные действия также нельзя.)
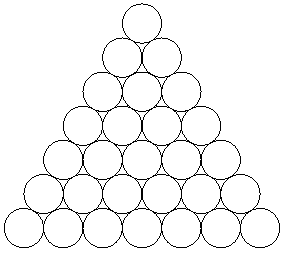
4. Как закрасить пять кружков на рисунке таким образом, чтобы никакие два закрашенных кружка не находились на одной горизонтали, а также не находились на прямой, параллельной одной из двух других сторон треугольника?

5. В некотором месяце три воскресенья пришлись на чётные числа. Каким днём недели было двадцатое число этого месяца? Укажите все варианты.