6. Найдите сумму
1/(1 x 3)+1/(3 x 5)+...+1/(997 x 999).
(Знак x обозначает умножение.)
7. В каком отношении нужно смешать трёхпроцентный и тридцатипроцентный растворы кислоты, чтобы получить двенадцатипроцентный раствор?
8. Можно ли разрезать какой-либо тупоугольный треугольник на несколько остроугольных? (Приведите пример или докажите, что это невозможно.)
9. Можно ли число 203 представить в виде суммы нескольких натуральных чисел (не обязательно различных), произведение которых тоже равно 203?
10. Один выпуклый четырехугольник расположен внутри другого. Может ли сумма диагоналей внутреннего быть больше суммы диагоналей внешнего? Объясните свой ответ.
11. Натуральное число a увеличили на 1, при этом его квадрат увеличился на 1001. Чему равно a?
12. Какое наименьшее число распилов необходимо, чтобы распилить куб со стороной 3 см на 27 кубиков со стороной 1 см? (Распил производится по плоскости; части разрешается перекладывать и пилить сразу несколько частей.) Докажите, что нельзя обойтись меньшим числом распилов.
13. На доске были написаны 4 числа. Их сложили всевозможными способами по два и получили следующие шесть сумм: 2, 4, 9, 9, 14, 16. Какие числа были написаны на доске? Укажите все варианты.
14. Трава на всем лугу растет одинаково густо и быстро. Известно, что 70 коров поели бы ее всю за 24 дня, а 30 коров - за 60 дней. Сколько коров поели бы всю траву на лугу за 96 дней?
15. При сложении двух целых чисел Коля поставил лишний ноль на конце первого слагаемого и получил в сумме 6641 вместо 2411. Какие числа он складывал?
16. Верно ли, что число 3999991 простое (т.е. делится только на единицу и на себя)?
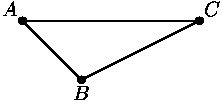
17. Сколько способами можно приставить к треугольнику ABC на рисунке ещё один треугольник так, чтобы они не перекрывались и вместе составляли равнобедренный треугольник?

18. Можно ли выписать в строчку 24 числа так, чтобы сумма любых трёх соседних чисел была положительна, а сумма всех чисел отрицательна? (Приведите пример или докажите, что это невозможно.)
19. (Продолжение) Тот же вопрос для 25 чисел.
20. Из одной вершины куба проведены две диагонали его граней. Какой угол они образуют?
21. Известно, что из утверждений "число A делится на 2", "число A делится на 4", "число A делится на 8", "число A делится на 16" три верных, а одно неверное. Какое именно утверждение неверно?
22. Произведение всех натуральных чисел от 1001 до 2007 разложили на простые множители. Сколько раз входит в это разложение множитель 2?
23. Как погрузить 21 бочку, из которых 7 полны кваса, 7 пусты, а 7 заполнены наполовину, на три грузовика, чтобы на всех грузовиках было поровну бочек и кваса? Переливать квас из одной бочки в другую не разрешается.
24. Сколько делителей имеет число 210 x 315 x 520? (Знак x означает умножение.)
25. В таблицу 20 x 20 записано 400 чисел, сумма которых неотрицательна. Докажите, что можно так переставить столбцы таблицы, чтобы сумма двадцати чисел на диагонали, идущей из левого верхнего угла таблицы в правый нижний угол, стала неотрицательной.