6. Восстановите равенство: *1*** x 233 = 7***065 (каждая звёздочка обозначает цифру, x обозначает умножение).
7. Имеется автомат с двумя кнопками и экраном. Сначала на экране горит число 0. При нажатии на одну кнопку число на экране увеличивается в 3 раза. При нажатии на вторую кнопку число увеличивается в 3 раза и прибавляется 1. Можно ли получить на экране число 328?
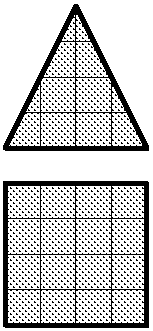
8. На стене с квадратным окном нужно повесить флажок в форме треугольника (см. рисунок) так, чтобы он не загораживал окна. Нарисовать, в каких точках можно вбивать гвоздик (флажок крепится на гвоздик в верхнем и висит ровно). Стена неограничена в размерах.

9. Бывают ли натуральные числа, произведение цифр которых равно 1998? Приведите пример или докажите, что не бывают.
10. На квадратной доске шириной 200 клеток и высотой 100 клеток в поле (1,1) (левый нижний угол) стоит фишка. За один шаг её передвигают в соседнюю по горизонтали или вертикали клетку. Сначала её двигают вправо: (1,1) - (2,1) - (3,1) - ... - (200,1), потом вверх (200,1) - (200,2) - ... - (200,100) и так далее по спирали (дойдя до границы или до уже пройденных клеток, фишка поворачивает налево). В какой клетке она окажется, когда посетит все клетки по одному разу? сколько шагов она сделает к этому моменту?
11. Сколько существует трехзначных чисел от 100 до 999, у которых первая и последняя цифра различаются на единицу?
12. Найдите целые положительные числа a, b, c, для которых НОК(a,b) = 210, НОД(a,b) = 10, НОК(a,c) = 110, НОД(a,c) = 2. (Здесь НОК(u,v) - наименьшее общее кратное u и v, то есть наименьшее целое число, делящееся нацело на u и v, а НОД(u,v) - наибольший общий делитель чисел u и v, то есть наибольшее целое число, на которое u и v делятся без остатка.)
13. Сколько существует пар (x,y) целых чисел, для которых |x| + |y| < 100?
14. Известно, что число A - k3 делится на 27 - k при любом k, не равном 27. Найдите все значения, которые может принимать A, и докажите, что других нет.
15. Найдите все целые положительные x и y, при которых x! + 12 = y2, и докажите, что других нет.
16. Приведите пример двух положительных чисел, разность которых равна их произведению.
17. На доске написано 25 чисел. Какие бы три из них мы ни выбрали, всегда можно выбрать ещё одно, чтобы сумма этих четырёх чисел была положительна. Верно ли, что сумма всех чисел положительна? Обоснуйте свой ответ.
18. Чему равно произведение (1 - 1/4)(1 - 1/9)(1 - 1/16)...(1 - 1/225)?
19. Составьте квадрат из 31 квадратной плитки: четырёх плиток размером 1 x 1, восьми плиток размером 2 x 2, двенадцати плиток размером 3 x 3 и семи плиток размером 4 x 4.
20. Вася плавает в центре квадратного бассейна. Внезапно к вершине квадрата подошёл Васин папа, который не умеет плавать, но бегает в 4 раза быстрее, чем плавает Вася. Вася бегает быстрее папы. Сможет ли он убежать?
21. 100 шестиклассников, 99 семиклассников и 101 восьмиклассник играли в пейнтбол по странным правилам. Шестиклассники могут стрелять только в восьмиклассников, восьмиклассники - только в семиклассников, а семиклассники - только в шестиклассников. Тот, в кого попали, выбывает из игры. Нельзя стрелять в того, кто сделал нечётное число удачных выстрелов. Они играли до тех пор, пока не остался один победитель. В каком классе он учится?
22. В таблице m x n разрешается у всех чисел одной строки или у всех чисел одного столбца изменить знак. Докажите, что несколькими такими заменами можно добиться того, чтобы сумма чисел в каждом столбце и в каждой строке была неотрицательна.
23. Сто грустных мартышек кидаются друг в друга одним кокосовым орехом. Грустная мартышка, попавшая орехом в другую грустную мартышку, становится весёлой и уже больше не грустнеет (хотя всё равно может кидаться орехом). Мартышка, в которую попали, выбывает из игры. Каких мартышек больше выбыло из игры - весёлых или грустных - к моменту, когда в игре осталась одна мартышка?
24. При дворе короля Артура собралось 2k рыцарей, причём каждый из них имеет среди присутствующих не более k - 1 врага. Докажите, что рыцарей можно рассадить за круглым столом так, что ни один из них не будет сидеть рядом со своим врагом.
25. Три последовательных двузначных числа выписали друг за другом. Оказалось, что полученное шестизначное число делится на 17. Каким могло быть это шестизначное число? Укажите все варианты.