6. Маша ест кашу через день, по одной тарелке в день. В этом месяце она съела на две тарелки каши меньше, чем в прошлом. Сколько тарелок каши она съела в этом месяце и сколько съест в следующем? Укажите все варианты.
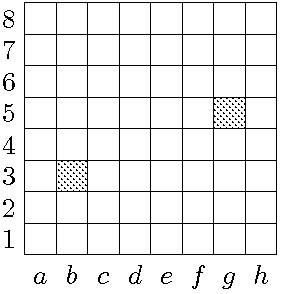
7. Шахматный король находится на поле b3 и хочет попасть на поле g5, сделав минимальное число ходов. (За один ход он может перейти в соседнюю клетку по вертикали, горизонтали или диагонали.) Отметьте все клетки шахматной доски, которые могут встретиться на таком (кратчайшем) пути.

8. На упаковке написано, что творог содержит 6% жира, или 40% жира в сухом веществе. Каков процент воды в таком твороге?
9. На полу лежат два квадратных коврика: размером 1x1 и 2x2, причём угол большего коврика попадает в центр меньшего. Какова общая площадь покрытой ковриками части пола? Укажите минимально и максимально возможные значения.
10. После стирки 100 пар носков (все пары разные) носки разложили произвольным образом по двум мешкам. В одном окалось 42 пар носков и 17 непарных. Сколько пар оказалось в другом мешке?
11. После стирки 100 пар носков (все пары разные) носки разложили произвольным образом по трём мешкам, в одном оказалось 32 пары и 6 непарных, в другом 35 пар и 31 непарный. Сколько непарных могло быть в третьем мешке? Укажите все возможности.
12. Целое положительное число увеличили на 3, отчего его сумма цифр уменьшилась на 47. Возможно ли это? (Если нет, докажите, что невозможно, если да - укажите наименьшее число с таким свойством.)
13. (Продолжение) Тот же вопрос, если сумма цифр уменьшилась на 96.
14. В пикнике участвовали 8 человек, которые решили поделить расходы поровну. Подсчитав впоследствии, кто сколько потратил, они установили, что трое потратили больше среднего на 500 рублей (каждый), а пятеро потратили меньше среднего на 300 рублей (каждый). Они хотят произвести взаиморасчёты с помощью переводов (любой участник может бесплатно перевести любую сумму любому другому). Какое минимальное количество переводов потребуется? Укажите оптимальный вариант.
15. (Продолжение) Докажите, что меньшим числом переводов обойтись нельзя.
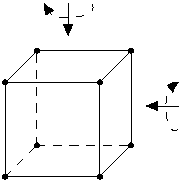
16. Куб повернули на 90 градусов вокруг горизонтальной оси, затем на 90 градусов вокруг вертикальной оси (см. рисунок), потом снова на 90 градусов вокруг горизонтальной оси, потом - вертикальной, и так далее. Вернётся ли куб в исходное положение и если да, то через сколько поворотов?
17. Трёхзначное число делится на 7, сумма его цифр делится на 7 и все цифры разные. Найдите все такие числа.
18. Положительное целое число делится на 18, а после прибавления единицы будет делиться на 17. Может ли так быть?
19. Известно, что 1 ≤ x ≤ 4 и 2 ≤ y ≤ 3. Какие значения может принимать дробь (x-y)/(x+y), а какие - не может?
20. Можно ли шахматную доску 8x8 разрезать по сторонам клеток на 11 частей так, чтобы никакие две части не содержали поровну клеток? Объясните свой ответ.
21. Какая из двух сумм больше:
1/51 + 1/52 + ... + 1/100 или 1/501 + 1/502 + ... + 1/1000?