Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 18 марта выслать полные решения задач по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника (см. на обороте).
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/.
Желаем успеха!
1. Каждую сторону прямоугольника увеличили на 1 см; в результате его площадь увеличилась на 39 см2. Потом каждую сторону прямоугольника увеличили ещё на 1 см. На сколько на этот раз увеличилась его площадь? (Укажите все возможные варианты ответа, если их несколько.)
2. Напишите какое-нибудь трёхзначное число с таким свойством: с любым из чисел 743, 145 и 765 оно совпадает ровно в одном разряде (единиц, десятков или сотен).
3. Существует ли треугольник, в котором сумма любых двух углов больше 125°? Объясните свой ответ.
4. Найдите самое большое целое число, при делении которого на 2012 частное и остаток получаются равными. Объясните, почему больше быть не может.
5. При проверке контрольной из пяти задач выяснилось, что каждую задачу решило нечётное число школьников, а каждый школьник решил нечётное число задач. Чётное или нечётное число школьников участвовали в контрольной? (Требуется не только ответ, но и доказательство.)
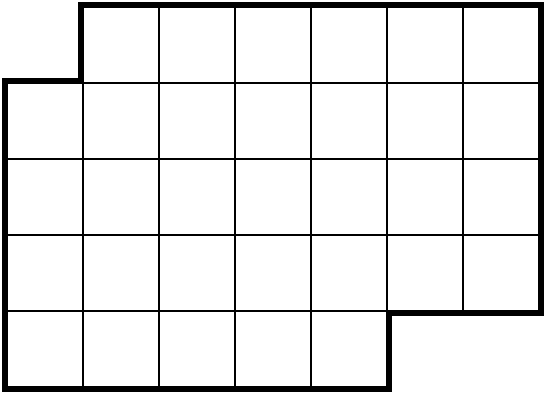
6. Разрежьте фигуру на рисунке на две равные (по форме и величине) части. Линия разреза должна проходить по границам клеток.
7. Укажите какое-нибудь целое число k>1, для которого число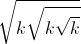 
тоже будет целым числом.
8. Часы со стрелками идут равномерно, при этом минутная стрелка обгоняет часовую каждые 65 минут (ровно). Спешат они или отстают? Выставим точное время на них в начале года (в полночь) — когда они покажут точное время в следующий раз?
9. Как разрезать квадрат на 20 равных треугольников, если разрезы, параллельные сторонам квадрата, проводить запрещается?
10. На сколько частей делят пространство четыре плоскости ABC, ABD, BCD, ACD, являющиеся гранями пирамиды ABCD?
11. Трём мудрецам сказали, что на каждого из них наденут чёрную или белую шляпу (цвет не виден), а потом всех трёх соберут в одной комнате (каждый увидит шляпы двух других мудрецов) и спросят, какие на них шляпы. Каждый мудрец должен написать на бумажке одно из слов «чёрная», «белая» или «не знаю», не показывая бумажку другим. Мудрецы выиграют, если (1) ни один из них не даст неправильного ответа и (2) хотя бы один отгадает цвет своей шляпы. Как им сговориться действовать, чтобы выиграть в 75% случаев (для 6 из 8 возможных вариантов)?
12. Петя хочет выбрать среди чисел 1, 2, ..., 2012 как можно больше, но нельзя, чтобы отношение каких-либо двух выбранных чисел было целой степенью тройки (3, 9, 27, ...). Как это сделать и почему предложенный вариант — наилучший?
13. В квадрате 10x10 расположены 99 фигур площади 99 (каждая). Докажите, что существует точка, принадлежащая всем 99 фигурам.
14. Докажите, что в последовательности чисел 1, 2, 4, 7, 13, 24, ... (каждое следующее число равно сумме трёх предыдущих) есть число, оканчивающееся четырьмя нулями.
15. На большом листе клетчатой бумаги 20 клеток окрашены в чёрный цвет, остальные белые. Каждую секунду происходит перекрашивание клеток, при этом каждая клетка приобретает цвет большинства из трёх клеток: её самой и двух её соседей сверху и справа (скажем, если сейчас клетка белая, а два её соседа чёрные, то на следующем шаге она будет чёрной). Докажите, что через некоторое время все клетки станут белыми.
16. (Продолжение) Докажите, что это случится уже через 20 секунд (после 20 перекрашиваний).
17. По кругу написано четыре целых числа. На каждом шаге между соседними числами пишут их разность (большее минус меньшее), а сами числа стирают. Докажите, что через некоторое время все числа станут чётными.
18. (Продолжение) Докажите, что через некоторое время все числа станут равны нулю.
19. Какое максимальное число ладей можно разместить квадратной доске 100x100, чтобы каждая из них стояла под ударом не более чем одной из остальных?
20. На шахматной доске стоят 11 пешек, причём их расположение симметрично относительно одной из диагоналей доски. Докажите, что одна из пешек стоит на этой диагонали.