Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 25 февраля выслать полные решения задач обычным письмом (не заказным) по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника (см. на обороте).
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/. В частности, на этом сайте будет указана дата разбора задач (скорее всего, это будет в мае), а после разбора помещён список победителей конкурса.
На сайте http://www.mccme.ru/ имеется также информация о математических кружках, олимпиадах и пр. Информацию о кружках можно получить также по телефону (499) 241-05-00.
Желаем успеха!
1. Каждую неделю Витя получает в школе три оценки (целое число от 2 до 5): одну по математике, одну по физике и одну по русскому языку. Родители хвалят его, если по большинству предметов его оценка повысилась по сравнению с предыдущей неделей. Какое максимальное число недель подряд его могут хвалить?
2. Сумма цифр натурального числа A равна B, а сумма цифр числа B равна C. Может ли сумма A+B+C равняться 165?
3. Один круг вписан в равносторонний треугольник, а другой описан вокруг него (см. рисунок). Что больше по площади: серая часть на рисунке или меньший круг? Объясните свой ответ.
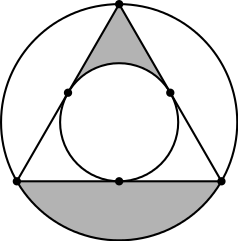
4. Лыжники выходят со старта с интервалами в 10 минут и идут в гору (с одной и той же скоростью). Дойдя до вершины, они поворачивают назад и возвращаются с большей (но тоже одинаковой у всех) скоростью. Идя в гору, лыжник встречает возвращающихся коллег каждые 6 минут. Как часто он будет встречать идущих в гору на обратном пути? Во сколько раз скорость при движении вниз больше, чем при движении вверх?
5. Квадратная доска m×n разбита на клетки. Ладья, проходя по горизонтали и вертикали (как в шахматах) обходит все клетки по одному разу и возвращается в исходную клетку. Отметим путь ладьи (несамопересекающаяся ломаная, проходящая через центры клеток; на рисунке показан один из множества вариантов). Какова может быть длина этой ломаной? (Зависит ли она от того, как именно движется ладья? Дайте обоснованный ответ.)

6. (Продолжение) Тот же вопрос для площади многоугольника, ограничиваемого этой ломаной.
7. На доске написаны два числа: 11 и 13. Многократно выполняется такая операция: одно из чисел на доске уменьшается на 1, а другое списывается в тетрадку. Так делается, пока оба числа не станут нулями. Сколько чисел будет написано в тетрадке? Какова будет сумма этих чисел? (Укажите все варианты ответов, и докажите, что других нет.)
8. На полу нарисован круг, и есть несколько круглых плиток того же размера. Можно ли положить 5 плиток так, чтобы они не перекрывались друг с другом, но чтобы каждая накрывала часть круга на полу (пусть маленькую, но ненулевую)? Тот же вопрос для 6 и 7 плиток.
9. На полу нарисован квадрат, и есть несколько квадратных плиток того же размера. Можно ли положить 5 плиток так, чтобы они не перекрывались друг с другом, но чтобы каждая накрывала часть квадрата на полу (пусть маленькую, но ненулевую)? Тот же вопрос для 6 и 7 плиток.
10. Тринадцать мячей разного размера лежали в 13 коробках. Мячи вынули из коробок. Когда их стали укладывать назад, коробки перепутались (мяч мог попасть не в свою коробку, а в бо́льшую), и некоторые мячи остались без коробок (не помещались в свободные). Какое наибольшее число мячей могло остаться без коробок? Объясните свой ответ.
11. На бумаге чернилами нарисовали окружность диаметром 10см, после чего прокатили по бумаге цилиндр из впитывающей чернила промокашки (длина окружности цилиндра — 3см). Окружность отпечатала на цилиндре линию. Сколько у этой линии точек самопересечения (в которых два участка кривой пересекаются)?
12. На дом задали выписать все варианты представления числа 8 в виде суммы целых положительных слагаемых (порядок слагаемых не важен), и Вова нашёл такие варианты: 8, 2+6, 1+4+3, 3+5, 2+1+5, 2+1+1+2+1+1, 1+6+1, 4+4, 3+1+1+1+1+1, 2+2+4, 1+1+1+1+1+1+1+1, 1+1+1+4+1, 2+2+2+2, 3+2+3, 1+2+3+2, 1+1+1+3+2, 7+1, 1+2+1+4, 1+2+1+2+2, 5+1+1+1, 1+1+1+1+1+1+2. Пропустил ли он какие-то варианты? Если да, то какие?
13. По плоскости катают (без проскальзывания) кубик: вправо – вверх – влево – вниз – вправо – вверх – влево – вниз и так далее. Вернётся ли он в исходное положение (это означает, что каждая вершина кубика окажется на прежнем месте), и если да, то через сколько перекатываний?
14. В узлах (точках пересечения горизонталей и вертикалей) клетчатой бумаги выбрано 5 точек. Докажите, что середина отрезка, соединяющего некоторые две из них, также попадает в узел.
15. Найдите сумму всех пятизначных чисел, в которых встречаются только цифры 1, 3 и 4 (не обязательно все).
16. По листу клетчатой бумаги размером 30 на 45 клеток провели прямую. Какое наибольшее число клеток она может пересечь? (Пересечение означает, что прямая проходит внутри клетки; пересечение с границей не считается.)
17. Существует ли целое положительное число, кроме 1, при делении на которое числа 123, 180 и 275 дают одинаковые остатки?
18. Имеется 100 монет, среди которых нет двух одного веса, и весы с чашками, на которые можно положить по монете, и весы покажут, какая из двух положенных на чашки монет тяжелее. Как, сделав 148 взвешиваний, найти и самую лёгкую, и самую тяжёлую монеты?
19. В фанерном круге в каком-то месте просверлили дырку. Всегда ли можно распилить этот круг на две части, сделав разрез по дуге окружности, и заново склеить из них круг, в котором просверленная дырка окажется в центре?
20. В таблице 3×3 расставлены числа. Произведение чисел в каждой строке и в каждом столбце равно a ≠ 0, а произведение чисел в любом из четырёх квадратов 2×2 равно b. Какое число стоит в центральной клетке?