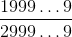, в числителе и знаменателе которой по сто девяток. Витя приписал ещё по девятке в конец числителя и знаменателя (так что и там, и там стало по 101 девятке). Увеличилась ли от этого дробь или уменьшилась?Дорогой друг!
Приглашаем тебя принять участие в заочном конкурсе по математике и информатике. Участвовать в нём может любой ученик 6-8 класса, решивший по крайней мере пять из предлагаемых 20 задач. Для этого он должен не позднее 15 марта выслать полные решения задач обычным письмом (не заказным) по адресу
Москва, 119002, Большой Власьевский пер., дом 11, Московский центр непрерывного математического образования, заочный конкурс, ... класс.
На письме должен быть указан обратный адрес, включая имя и фамилию. В письмо следует вложить два пустых незаклеенных конверта с маркой, написав на них свой адрес (В одном конверте будут посланы результаты проверки и приглашение на разбор. Другой конверт может быть использован для информации о заочном конкурсе, математических кружках, олимпиадах и пр.)
На каждом листе работы просим указывать фамилию, имя, номер школы и класс. В письмо следует вложить заполненную карточку участника.
Справки по всем вопросам, связанным с конкурсом, можно получить по телефону (495) 945-82-16 (попросить соединить с организаторами заочного конкурса), а также по электронной почте: zmk@mccme.ru. (Очень просим Вас НЕ присылать решения по электронной почте.) Информация о заочном конкурсе имеется в Internet на сайте http://www.mccme.ru/zmk/. В частности, на этом сайте будет указана дата разбора задач (скорее всего, это будет в мае), а после разбора помещён список победителей конкурса.
На сайте http://www.mccme.ru/ имеется также информация о математических кружках, олимпиадах и пр. Информацию о кружках можно получить также по телефону (499) 241-05-00.
Желаем успеха!
1. Придумайте, как нарисовать два несамопересекающихся пятиугольника так, чтобы у них были одни и те же вершины, но не было ни одной общей стороны.
2. При каком наименьшем n произведение всех чисел от 1 до n (то есть число 1·2·3·…·n) делится нацело на 2015?
3. Два двузначных числа в сумме дают 87. В каждом из них поменяли местами цифры (число десятков стало числом единиц и наоборот) и полученные числа сложили. Какая сумма могла получиться? Укажите все возможные варианты и докажите, что других нет.
4. На доске написана дробь 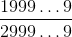, в числителе и знаменателе которой по сто девяток. Витя приписал ещё по девятке в конец числителя и знаменателя (так что и там, и там стало по 101 девятке). Увеличилась ли от этого дробь или уменьшилась?
5. Шахматный конь стоит на поле a1 (угловое поле доски 8×8). Двое игроков по очереди делают ходы. Тот, кто пошёл на клетку, где конь уже был, проигрывает. Кто выигрывает при правильной игре, и как он должен играть?
6. В бригаде маляров один умеет красить доски забора через одну (одну покрасит, следующую пропускает, следующую красит, и так далее), второй умеет красить доски забора через две (одну покрасит, две пропустит, следующую покрасит, и так далее), третий через три, четвёртый через четыре, …, сотый — через сто. Можно ли с их помощью покрасить забор из тысячи досок целиком? (Каждый маляр получает только одно задание, одну и ту же доску можно красить много раз.)
7. Известно, что сумма числителя и знаменателя дроби равна 52 (числитель и знаменатель — целые положительные числа), а сама дробь меньше 3/5. Сколько существует таких дробей?
8. Самолёт вылетает из города А в 08:00 и прилетает в город Б в 10:00. Обратно он вылетает из города Б в 12:00 и прилетает в город А в 18:00. При этом полёт в обе стороны продолжается одно и то же время. Какое?
9. Вершины правильного 2n-угольника произвольным образом раскрашены в два цвета — есть n синих и n зелёных. Докажите, что количество диагоналей данной длины, у которых оба конца синие, равно количеству диагоналей той же длины, у которых оба конца зелёные.
10. Три колодца находятся в вершинах равностороннего треугольника ABC со стороной 1. Нарисуйте, где находятся точки, для которых колодец A является ближайшим. Где находятся точки, для которых A является самым дальним? Где находятся точки, для которых A не ближайший и не самый дальний?
11. Купец купил лошадь за 10 рублей, затем продал за 12, решил, что продешевил, выкупил за 15 и, наконец, продал за 19. Сколько всего денег он на этом заработал?
12. По кругу в произвольном порядке расставлены цифры 0, 1, 2, 3, …, 9, каждая по одному разу. Для каждой пары соседних цифр подсчитали их разницу (положительное число), и все эти числа сложили. Какой наименьший результат мог получиться? Приведите пример такой расстановки и покажите, что меньше быть не может.
13. (Продолжение) Сколько существует вариантов размещения цифр предыдущей задачи, для которых достигается минимум суммы расстояний между соседними цифрами? (Варианты, отличающиеся друг от друга лишь поворотом, считаются за один.)
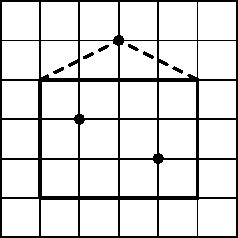
14. На стене имеются два грязных пятна (точки). Вася хочет повесить прямоугольную картину так, чтобы она закрыла оба этих пятна. Для этого он вбивает в стену гвоздь и вешает картину за середину верёвки. (Одно из возможных положений гвоздя показано на рисунке; верёвка изображена пунктиром.) На этом же рисунке покажите все точки стены, куда можно вбить гвоздь и добиться желаемого.
15. Представьте число 19 в виде суммы нескольких целых положительных слагаемых, причём таким образом, чтобы произведение этих слагаемых было максимально возможным. Объясните, почему ваш вариант наилучший.
16. На столе стояли 100 стаканов. Каждый второй стакан (то есть стаканы с номерами 2, 4, 6, …, 100) перевернули. Затем перевернули каждый третий (3, 6, …, 99) стакан, затем каждый четвертый, …, каждый сотый (при этом перевернулся только один, сотый, стакан). Сколько стаканов окажутся в конце концов перевернутыми вверх дном? Стаканы с какими номерами вернутся в исходное положение?
17. Шахматные доски (квадраты 8×8 из клеток 1×1) приложены друг к другу сторонами так, что они образуют одну большую (бесконечную во все стороны) доску. В каждой доске выпилена клетка a1. Может ли шахматный конь, начав с одной из клеток, двигаться так, чтобы в итоге (рано или поздно) побывать в каждой невыпиленной клетке ровно по одному разу?
18. Если каждую из семи полученных Васей за год двоек исправить на тройку, то его средняя оценка увеличится ровно на 1/5. Сколько не-двоек получил Вася за год?
19. Напишем подряд числа 1, 2, 3, 4, …, 2014, 2015. Каких цифр при этом использовано больше — двоек или троек? На сколько?
20. Все грани многогранника — треугольники. В каждой вершине многогранника написано число. Докажите, что количество граней, у которых все три числа в вершинах разные, чётно.