Математическое образование: вчера, сегодня, завтра…

Арнольд Владимир Игоревич
"Жесткие" и "мягкие" математические модели

3. Жесткие модели как путь к ошибочным предсказаниям

Важно, чтобы простейшая модель была структурно устойчивой, т. е. чтобы выводы выдерживали малое изменение параметров и функций, описывающих модель. Описанная выше модель обладает этим свойством структурной устойчивости. Пример модели, не обладающей этим свойством, -- знаменитая модель Лотка-Вольтерра борьбы за существование (рис. 8),

=ax-cxy,
= -by+dxy.

В этой модели x -- число карасей, y -- число щук (желающие могут считать, что x -- трудящиеся, а y -- организованные преступники). Коэффициент a описывает скорость естественного прироста числа карасей в отсутствие щук, b -- естественное вымирание щук, лишенных карасей. Вероятность взаимодействия карася и щуки считается пропорциональной как количеству карасей, так и числу щук (xy). Каждый акт взаимодействия уменьшает популяцию карасей, но способствует увеличению популяции щук (члены -cxy и dxy в правой части уравнения).


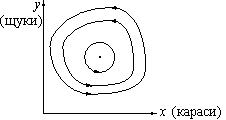Рис. 8. Эволюция популяции карасей и щук в модели Лотка-Вольтерра.

Математический анализ этой (жесткой) модели показывает, что имеется стационарное состояние (A на рис. 8), всякое же другое начальное состояние (B) приводит к периодическому колебанию численности как карасей, так и щук, так что по прошествии некоторого времени система возвращается в состояние B.

При малом изменении модели

=ax-cxy+ef(x,y),
= -by+dxy+eg(x,y),   e<<1,

к правым частям добавляются малые члены (учитывающие, например, конкуренцию карасей за пищу и щук за карасей). В результате вывод о периодичности (возвращении системы в исходное состояние B), справедливый для жесткой системы Лотка-Вольтерра, теряет силу. В зависимости от вида малых поправок f и g возможны, например, сценарии 1-3 рис. 9 (которые уже структурно устойчивы).


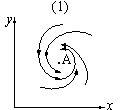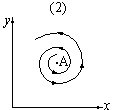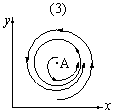Рис. 9. Мягкая структурно устойчивая модель борьбы за существование.

В случае 1 равновесное состояние A устойчиво. При любых других начальных условиях через большое время устанавливается именно оно.

В случае 2 система " идет в разнос". Стационарное состояние неустойчиво. Эволюция приводит то к резкому увеличению числа бандитов, то к их почти полному вымиранию (вследствие того, что они настолько ограбили трудящихся, что взять уже нечего). Такая система в конце концов попадает в область столь больших или столь малых значений x и y, что модель перестает быть применимой: происходит изменение законов эволюции, т. е. революция.

В случае 3 в системе с неустойчивым стационарным состоянием A устанавливается с течением времени периодический режим C (в котором, скажем, радикалы и консерваторы периодически сменяют друг друга). В отличие от исходной жесткой модели Лотка-Вольтерра, в этой модели установившийся периодический режим не зависит от начального условия. Первоначально незначительное отклонение от стационарного состояния A приводит не к малым колебаниям около A, как в модели Лотка-Вольтерра, а к колебаниям вполне определенной (и не зависящей от малости отклонения) амплитуды. Возможны и другие структурно устойчивые сценарии (например, с несколькими периодическими режимами).

Вывод: жесткую модель всегда надлежит исследовать на структурную устойчивость полученных при ее изучении результатов по отношению к малым изменениям модели (делающим ее мягкой).

В случае модели Лотка-Вольтерра для суждения о том, какой же из сценариев 1-3 (или иных возможных) реализуется в данной системе, совершенно необходима дополнительная информация о системе (о виде малых поправок f и g в нашей формуле). Математическая теория мягких моделей указывает, какую именно информацию для этого нужно иметь. Без этой информации жесткая модель может привести к качественно ошибочным предсказаниям. Доверять выводам, сделанным на основании жесткой модели, можно лишь тогда, когда они подтверждаются исследованием их структурной устойчивости.

Следующий раздел