Глава  30. § 1  |	Оглавление |

Дополнение

Кубические уравнения, связанные с треугольником

Для любого треугольника несложно доказать соотношение

p – a = r ctg (A/2),

где p - полупериметр, r - радиус вписанной окружности. В самом деле, пусть u = AC₁ = AB₁, v = BC₁ = BA₁, w = CA₁ = CB₁ (см. рис. 1). Тогда u + v = c, v + w = a, w + u = b. Поэтому

u =

b + c – a 2

= p – a.

Остается заметить, что AB₁ = r ctg (A/2).

Рис. 1

Воспользуемся теоремой синусов и заменим a на 2Rsin A, где R - радиус описанной окружности. В результате получим

p = 2Rsin A + r ctg (A/2).

Рассмотрим для треугольника с некоторыми значениями p,R и r уравнение

p = 2Rsin j + r ctg (j/2).

(1)

Это уравнение имеет корни j₁ = A, j₂ = B, j₃ = C - величины углов треугольника. Можно ожидать, что уравнение (1) в каком-то смысле является кубическим уравнением.

В уравнение (1) входят sin j и ctg (j/2). Их можно выразить через какую-нибудь одну тригонометрическую функцию. Например,

sin j  =   2tg (j/2) 1 + tg 2(j/2) ,   ctg (j/2) =   1 tg (j/2) .

Поэтому при x = tg (j/2) уравнение (1) принимает вид

p =   4Rx 1 + x2  +   r x ,

т. е.

x3 –   4R + r p x2 + x –   r p  = 0.

(2)

Уравнение (2) имеет корни x₁ = tg (A/2), x₂ = tg (B/2), x₃ = tg (C/2). В том случае, когда эти числа различны, по теореме Виета получаем

tg   A 2  + tg   B 2  + tg   C 2  =   4R + r p ,

tg   A 2 tg   B 2  + tg   B 2 tg   C 2  + tg   C 2 tg   A 2  = 1,

tg   A 2 tg   B 2 tg   C 2  =   r p .

С помощью предельного перехода легко убедиться, что эти формулы остаются справедливыми и в том случае, когда среди чисел tg (A/2), tg (B/2), tg (C/2) есть равные.

Выразим теперь sin j и ctg (j/2) через x = cos j:

sin j  =  Ц   1 – cos 2j    =  Ц   1 – x2   ,    ctg (j/2) =   sin j 1 – cos j  =  Ц 1 – x2 1 – x .

Подставив эти выражения в уравнение (1), получим

p =  Ц   1 – x2   ж и 2R +   r 1 – x ц ш .

При x № 1 это уравнение приводится к виду

x3 –  ж и 1 +   r R ц ш x2 +  ж и  p2 + r2 – 4R2 4R2 ц ш x –   p2 – (2R + r)2 4R2  = 0.

Следовательно,

cos A + cos B + cos C = 1 +   r R ,

cos Acos B + cos Bcos C + cos C + cos A =   p2 + r2 – 4R2 4R2 ,

cos A + cos B + cos C =   p2 – (2R + r)2 4R2 .

Легко проверить, что при x = 2Rsin j уравнение (1) принимает вид

x3 – 2px2 + (p2 + 4Rr + r2)x – 4Rrp = 0.

Поэтому

a + b + c = 2p,    ab + bc + ca = p2 + 4Rr + r2,    abc = 4Rrp.

Аналогичным образом sin j и tg (j/2) можно выражать через другие тригонометрические функции и подставлять эти выражения в уравнение (1).

При x = tg j получаем уравнение

(p2 – (2R + r)2)x3 – 2prx2 + (p2 – 4Rr – r2)x – 2pr = 0.

При x = sin ²(j/2) получаем уравнение

16R2x3 – 8R(2R – r)x2 + (p2 + r2 – 8Rr)x – r2 = 0.

При x = cos ²(j/2) получаем уравнение

16R2x3 – 8R(4R + r)x2 + (p2 + (4R + r)2)x – p2 = 0.

Точки пересечения диагоналей правильных многоугольников

Известно довольно много задач про треугольники с целочисленными углами. Вот два примера таких задач.

Задача 1. В равнобедренном треугольнике ABC с основанием BC угол при вершине A равен 80°. Внутри треугольника взята точка M так, что РMBC = 30° и РMCB = 10°. (См. рис. 2 a .) Доказать, что РAMC = 70°.

Задача 2. В равнобедренном треугольнике ABC с основанием AC угол при вершине B равен 20°. На сторонах BC и AB взяты точки D и E соответственно так, что РDAC = 60° и РECA = 50°. (См. рис. 2 б .) Доказать, что РADE = 30°.

Рис. 2

Задачи такого типа обычно бывают связаны с точками пересечения троек диагоналей правильных многоугольников, в данном случае - правильного восемнадцатиугольника.

Обратимся к рис. 3. Этот рисунок показывает, что задача 1 эквивалентна следующему утверждению:

в правильном восемнадцатиугольнике диагонали A₁A₁₃, A₃A₁₄ и A₆A₁₅ пересекаются в одной точке.

В самом деле, если эти диагонали пересекаются в некоторой точке M, то 

РA1MA6 =   1 2 (ИA1A6 + ИA13A15)  =  50° + 20° = 70°.

Ясно также, что углы треугольника A₁A₆A₁₄ равны 80°, 40°, 40° и РMA₁₄A₆ = 30°,  РMA₆A₁₄ = 10°.

Рис. 3 Рис. 4

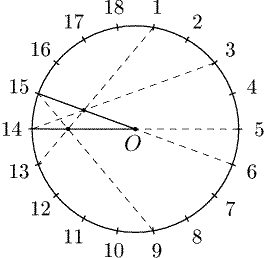
Рис. 5

Что же касается задачи 2, то она эквивалентна следующему утверждению: в правильном восемнадцатиугольнике диагонали A₁A₁₄, A₇A₁₆ и A₁₁A₁₇ пересекаются в одной точке (рис. 4).

Но задачу 2 можно решить и с помощью совсем другой тройки пересекающихся диагоналей, а именно, диагоналей A₁A₁₃, A₃A₁₄ и A₆A₁₅ (рис. 5). В качестве треугольника ABC мы берем треугольник A₁₄OA₁₅. Диагонали A₁A₁₃ и A₉A₁₅ симметричны относительно диаметра A₅A₁₄, поэтому обе диагонали пересекают диаметр в одной точке.

Но мы пока не доказали, что тройки диагоналей на рис. 3-5 действительно пересекаются в одной точке. Проверять, пересекаются ли тройки диагоналей в одной точке, удобно с помощью следующего утверждения.

Теорема. На сторонах треугольника ABC взяты точки A₁,B₁,C₁ (A₁ на BC и т. д. ). Отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке тогда и только тогда, когда

sin BAA1 sin CAA1  ·   sin ACC1 sin BCC1  ·   sin CBB1 sin ABB1  = 1.

Доказательство. Предположим сначала, что отрезки AA₁, BB₁ и CC₁ пересекаются в точке O (рис. 6). Тогда

2SAOB : 2SAOC = (AB · AOsin BAO) : (AC · AOsin CAO).

Следовательно,

1 =   SAOB SAOC  ·   SCOA SCOB  ·   SBOC SBOA  =  ж и  AB AC  ·   CA CB  ·   BC BA ц ш  sin BAO sin CAO  ·   sin ACO sin BCO  ·   sin CBO sin ABO ,

т. е.

sin BAA1 sin CAA1  ·   sin ACC1 sin BCC1  ·   sin CBB1 sin ABB1  = 1.

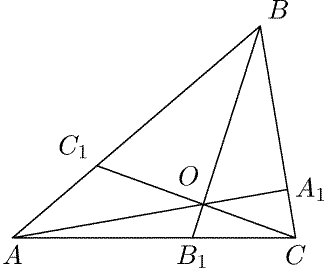
Рис. 6

Предположим теперь, что для точек A₁, B₁ и C₁ выполняется указанное соотношение. Пусть O - точка пересечения отрезков AA₁ и BB₁. Нужно доказать, что отрезок CC₁ проходит через точку O. Иными словами, если C₁ў - точка пересечения прямых CO и AB, то C₁ў = C₁. Отрезки AA₁,BB₁ и CC₁ў пересекаются в одной точке, поэтому, как только что было доказано,

sin BAA1 sin CAA1  ·   sin CBB1 sin ABB1  ·   sin ACC1ў sin BCC1ў  = 1.

Сравнив эту формулу с условием теоремы, получим

sin ACC1 : sin BCC1 = sin ACC1ў : sin BCC1ў.

Остается доказать, что при движении точки X по отрезку AB величина sin ACX : sin BCX изменяется монотонно. Сами углы РACX и РBCX изменяются монотонно, но их синусы могут быть не монотонными в случае тупого угла C. Это не беда. В любом треугольнике есть острый угол, и мы с самого начала могли бы взять в качестве угла C острый угол треугольника. Доказательство теоремы завершено. p

Теперь проверка того, что тройка диагоналей, изображенная на рис. 3, пересекается в одной точке, сводится к проверке тождества

sin 10° sin 70°  ·   sin 30° sin 20°  ·   sin 40° sin 10°  = 1.

Доказать его несложно:

sin 30°sin 40°  =   1 2 sin 40°  =  sin 20°cos 20° = sin 20°sin 70°.

Тройка диагоналей, изображенная на рис. 3, соответствует тождеству

sin 20°sin 40°sin 20°  =  sin 30°sin 60°sin 10°.

Есть еще три тождества, приводящих к тройкам пересекающихся диагоналей:

sin 10°sin 20°sin 80°  =  sin 20°sin 20°sin 30°,

sin 20°sin 30°sin 30°  =  sin 10°sin 40°sin 50°,

sin 10°sin 20°sin 30°  =  sin 10°sin 10°sin 100°.

Проверку этих тождеств мы оставляем читателю.

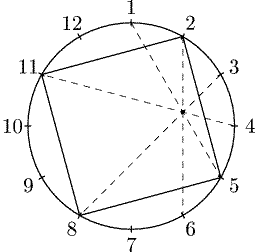
Рис. 7

Обратите внимание, что перестановка сомножителей в таких тождествах приводит к совсем другим тройкам пересекающихся диагоналей.

Наш интерес к восемнадцатиугольнику, а не к какому-либо другому правильному многоугольнику, связан с тем, что именно к нему приводят треугольники с углами, кратными 10°. Среди всех правильных многоугольников, число вершин которых меньше 18, интересные наборы пересекающихся диагоналей есть лишь у двенадцатиугольника. Например, диагонали A₁A₅, A₂A₆, A₃A₈ и A₄A₁₁ правильного двенадцатиугольника пересекаются в одной точке (рис. 7). Это утверждение эквивалентно следующей хорошо известной задаче.

Задача 3. Внутри квадрата ABCD взята точка P так, что треугольник ABP равносторонний. Доказать, что РPCD = 15°.

Упражнения.

а) На сторонах BA и AC взяты точки D и E так, что РDCB = РEBC = 40°. Доказать, что РAED = 30°.

б) На сторонах BA и BC взяты точки D и E так, что РDCA = 50° и РEAC = 40°. Доказать, что РAED = 30°.

2. В треугольнике ABC углы A,B и C равны 14°, 62° и 104°. На сторонах AC и AB взяты точки D и E соответственно так, что РDBC = 50° и РECB = 94°. Доказать, что РCED = 34°.

3. Доказать, что диагонали A₁A_n + 2, A_2n – 1A₃ и A_2nA₅ правильного 2n-угольника пересекаются в одной точке.

4. Доказать, что диагонали A₁A₇,A₃A₁₁ и A₅A₂₁ правильного 24-угольника пересекаются в точке, лежащей на диаметре A₄A₁₆.

5. Доказать, что в правильном тридцатиугольнике семь диагоналей

A1A13, A2A17, A3A21, A4A24, A5A26, A8A29, A10A30

пересекаются в одной точке.

Прямые Паскаля

В 1640 г. Блез Паскаль, которому было тогда 16 лет, напечатал в виде афиши тиражом 50 экземпляров свое сочинение «Опыт о кониках» («Essai sur les coniques»). Эти афиши были прибиты на стенах домов и розданы ученым. «Опыт о кониках» содержал несколько определений и лемм; доказательства отсутствовали. Основной теоремой этого сочинения была теорема о вписанном шестиугольнике. Эту теорему теперь называют теоремой Паскаля, а сам Паскаль, по свидетельству Лейбница, называл ее «мистическим шестиугольником» (Hexagramma mysticum). Эта теорема заключается в следующем. Если шестиугольник ABCDEF вписан в окружность, то точки пересечения продолжений его противоположных сторон (т. е. прямых AB и DE, BC и EF, CD и AF) лежат на одной прямой. Паскаль также отметил, что из этой теоремы с помощью центральной проекции можно получить аналогичное утверждение для шестиугольника, вписанного в произвольное коническое сечение (эллипс, параболу, гиперболу).

В теореме Паскаля шестиугольник ABCDEF не обязательно выпуклый; в данном случае шестиугольником можно считать произвольную замкнутую шестизвенную ломаную. Для шести фиксированных точек окружности существует ровно 60 замкнутых шестизвенных ломаных с вершинами в этих точках. В самом деле, выберем одну из шести точек; ее можно соединить с любой из пяти оставшихся точек, затем новую точку можно соединить с любой из четырех оставшихся точек и т. д. В результате получаем 5 · 4 · 3 · 2 = 120 различных вариантов, но при этом одну и ту же шестизвенную ломаную мы считаем дважды, так как при нашем способе подсчета учитывается и направление обхода ломаной. Таким образом, количество различных шестизвенных ломаных с вершинами в данных точках равно 120/2 = 60. Этим 60 шестизвенным ломаным соответствуют 60 прямых Паскаля. Якоб Штейнер (1827 г.) установил, что эти 60 прямых можно разбить на 20 троек прямых, пересекающихся в одной точке. Впоследствии Киркман (1850 г.) более детально исследовал конфигурацию 60 прямых Паскаля и установил, что помимо 20 точек Штейнера они пересекаются по три еще в 60 точках.

Известно много разных доказательств теоремы Паскаля, но все они не очень простые. Мы приведем одно из возможных доказательств, которое позволяет получить также и доказательства теорем Штейнера и Киркмана.

Введем для удобства следующее обозначение. Будем считать, что прямая AB задается уравнением l_AB = 0; это уравнение определено с точностью до пропорциональности. В координатах x,y функция l_AB имеет вид l_AB(x,y) = ax + by + c, причем l_AB обращается в нуль в точках A и B.

Лемма. Пусть точки A, B, C и D лежат на окружности, заданной уравнением второй степени f = 0. Тогда

f = llABlCD + mlBClAD,

где l и m - некоторые числа.

Первое доказательство. Пусть X - точка данной окружности, отличная от точек A,B,C и D. Выберем числа l₁ и m₁ так, что

l1lAB(X)lCD(X) + m1lBC(X)lAD(X) = 0,

и рассмотрим кривую, заданную уравнением f₁ = 0, где f₁ = l₁l_ABl_CD + m₁l_BCl_AD. Эта кривая задается уравнением второй степени и проходит через точки A, B, C, D и X. Но если кривая второй степени пересекает окружность в пяти различных точках, то эта кривая совпадает с окружностью, а значит, f = af₁, где a - некоторое число. p

Второе доказательство. Введем косоугольную систему координат с осями AB и AD. Тогда прямые AB и AD задаются уравнениями y = 0 и x = 0 соответственно, а уравнение f = 0, задающее окружность, является уравнением второй степени относительно x и y.

Ограничения функций f и ll_ABl_CD + ml_BCl_AD = lyl_CD + mxl_BC на любую из осей координат являются квадратными трехчленами с двумя общими корнями (A и B, или A и D). Поэтому числа l и m можно подобрать так, что многочлен

P(x,y) = f(x,y) – lylCD(x,y) – mxlBC(x,y)

обращается в нуль как при x = 0, так и при y = 0. Это означает, что он делится на xy, т. е. P(x,y) = qxy, где q - константа. В точке C многочлен P обращается в нуль, а xy № 0. Поэтому q = 0, т. е.

f = llABlCD + mlBClAD.        p

С помощью леммы мы докажем теоремы Паскаля, Штейнера и Киркмана. Рассмотрим шестиугольник ABCDEF, вершины которого лежат на окружности f = 0. Четырехугольники ABCD, AFED и BEFC вписаны в эту окружность, поэтому f можно представить в любом из следующих видов:

f = l1 lABlCD + m1 lADlBC,

(1)

f = l2 lAFlED + m2 lADlEF,

(2)

f = l3 lBElCF + m3 lBClEF.

(3)

Приравнивая выражения (1) и (2), получаем

l1 lABlCD – l2 lAFlED  =  (m1lBC – m2lEF)lAD.

Пусть X - точка пересечения прямых AB и ED. В точке X обращаются в нуль функции l_ABl_CD и l_AFl_ED, а функция l_AD в этой точке в нуль не обращается. Следовательно, в точке X обращается в нуль функция m₁l_BC – m₂l_EF, т. е. точка X лежит на прямой m₁l_BC = m₂l_EF. Аналогично доказывается, что точка пересечения прямых CD и AF лежит на прямой m₁l_BC = m₂l_EF. Очевидно также, что точка пересечения прямых BC и EF лежит на прямой m₁l_BC = m₂l_EF. В результате получаем следующее утверждение.

Теорема (Паскаль). Если точки A, B, C, D, E и F лежат на одной окружности, то точки пересечения прямых AB и DE, BC и EF, CD и FA лежат на одной прямой.

Но продолжим рассуждения дальше. Приравнивая (2) и (3), получим, что точки пересечения прямых AF и BE,  ED и CF,  AD и BC лежат на прямой m₂l_AD = m₃l_BC. А приравняв (1) и (3), получим, что точки пересечения прямых AB и CF,  CD и BE,  AD и EF лежат на прямой m₁l_AD = m₃l_EF. Легко проверить, что полученные прямые

m1lBC = m2lEF,   m2lAD = m3lBC,   m1lAD = m3lEF

пересекаются в одной точке. В самом деле, если X - точка пересечения первых двух из этих прямых, то 

m1m2lBC(X)lAD(X) = m2m3lEF(X)lBC(X).

Сократив на m₂l_BC(X), получим m₁l_AD = m₃l_EF (мы не будем останавливаться на обсуждении вырожденного случая, когда m₂l_BC(X) = 0).

Будем называть прямой Паскаля шестиугольника, вписанного в окружность, прямую, на которой лежат точки пересечения пар его противоположных сторон. При этом, как мы уже говорили, шестиугольником можно считать и замкнутую самопересекающуюся ломаную. Доказанное выше утверждение можно сформулировать следующим образом.

Теорема Штейнера. Пусть точки A, B, C, D, E и F лежат на одной окружности. Тогда прямые Паскаля шестиугольников ABCDEF, ADEBCF и ADCFEB пересекаются в одной точке.

Напомним, что при доказательстве этой теоремы исходными четырехугольниками были ABCD, AFED и BEFC. Можно исходить также из четырехугольников ABFE, ABDC и CDFE. Тогда получим следующее утверждение.

Теорема Киркмана. Пусть точки A, B, C, D, E и F лежат на одной окружности. Тогда прямые Паскаля шестиугольников ABFDCE, AEFBDC и ABDFEC пересекаются в одной точке.

Нетрудно убедиться, что каждая из 60 прямых Паскаля, соответствующих шести фиксированным точкам окружности, входит ровно в одну тройку Штейнера и в три тройки Киркмана.

Лемма, на которой было основано доказательство теорем Паскаля, Штейнера и Киркмана, бывает полезна и при доказательстве многих других геометрических теорем. Приведем два таких примера.

Самопересекающийся четырехугольник до некоторой степени похож на бабочку. С этим обстоятельством связаны названия следующих двух утверждений.

Теорема 1 (теорема о бабочке). Пусть хорды KL и MN проходят через середину O хорды AB. Тогда прямые KN и ML пересекают прямую AB в точках, равноудаленных от точки O.

Теорема 2 (теорема о двух бабочках). Пусть стороны самопересекающихся четырехугольников KLMN и KўLўMўNў, вписанных в одну и ту же окружность, пересекают хорду AB этой окружности в точках P,Q,R,S и Pў,Qў,Rў,Sў соответственно (сторона KL - в точке P, LM - в точке Q, и т. д.) Тогда если три из точек P,Q,R,S совпадают с соответственными тремя из точек Pў,Qў,Rў,Sў, то и оставшиеся две точки тоже совпадают. (Предполагается, что хорда AB не проходит через вершины четырехугольников.)

Доказательство теоремы о бабочке. Пусть f = 0 - уравнение данной окружности. Согласно лемме f = ll_KLl_MN + ml_KNl_ML. Это равенство выполняется и для ограничений всех рассматриваемых функций на прямую AB. Введем на прямой AB координату x, приняв точку O за начало координат. Тогда можно считать, что f = x² – a и l_KLl_MN = x², поэтому l_KNl_ML = bx² – c. Следовательно, корни уравнения l_KNl_ML = 0 равноудалены от точки O, что и требовалось. p

Доказательство теоремы о двух бабочках. Пусть для определенности P = Pў, Q = Qў и R = Rў. Согласно лемме

llKLlMN + mlKNlML = f  =  lўlKўLўlMўNў + mўlKўNўlMўLў.

Рассмотрев ограничение этого равенства на прямую AB, получим равенство вида

a(x - p)(x - r) + b(x - r)(x - s) = aў(x - p)(x - r) + bў(x - q)(x - sў).

(3)

При этом требуется доказать, что s = sў.

Равенство (3) можно преобразовать к виду

aўў(x – p)(x – r) = (x – q)[b(x – s) – bў(x – sў)].

Точка Q может совпасть только с точкой S, поэтому Q № P и Q № R, а значит, (x – p)(x – r) не делится на (x – q). Поэтому b(x – s) – bў(x – sў) = 0. Следовательно, s = sў. p

Кубические кривые, связанные с треугольником

Каждому треугольнику можно многими разными способами сопоставить кубическую кривую, т. е. кривую, заданную уравнением вида

е i + j Ј 3  aijxiyj = 0.

Некоторые из таких кубических кривых обладают интересными геометрическими свойствами. Эти кубические кривые, или кубики , обычно называют по именам геометров, впервые их исследовавших: кубика Дарбу, кубика Томсона, кубика Нейберга, кубика Мак-Кэя.

Наиболее интересные свойства кубик, связанных с треугольником, так или иначе используют изогональное сопряжение относительно этого треугольника. Поэтому наше изложение будет опираться на свойства изогонального сопряжения, о которых шла речь в предыдущем рассказе. Мы будем также пользоваться введенными там трилинейными координатами. Несложно понять, что в трилинейных координатах (x,y,z) кубическая кривая задается уравнением вида

е i + j + k = 3  cijkxiyjzk = 0.

Первоначально кубики, связанные с треугольником, определялись посредством разнообразных геометрических конструкций. Но наиболее известные из этих кубик можно получить единой конструкцией ¹.

Эта конструкция основывается на следующем утверждении.

Теорема. Пусть на плоскости задана точка F. Для данного треугольника ABC рассмотрим всевозможные пары изогонально сопряженных точек P и Q, для которых прямая PQ проходит через точку F. Тогда точки P и Q заметают кубическую кривую, которая проходит через вершины треугольника, через центры вписанной и трех вневписанных окружностей, а также через саму точку F.

Доказательство. Пусть точка F имеет трилинейные координаты (f₁,f₂,f₃). Если точка P имеет трилинейные координаты (x,y,z), то точка Q, изогонально сопряженная с ней, имеет трилинейные координаты (x ^– 1,y ^– 1,z ^– 1), т. е. (yz,zx,xy). Поэтому условие, что точки P,Q,F лежат на одной прямой, запишется в виде

к к к к f1 f2 f3 x y z yz zx xy к к к к  = 0,

т. е.

f1x(y2 - z2) + f2y(z2 - x2) + f3z(x2 - y2) = 0.

(1)

Легко проверить, что точка F = (f₁,f₂,f₃), точки A = (1,0,0), B = (0,1,0), C = (0,0,1) и точки I = (1,1,1), I_a = ( – 1,1,1), I_b = (1, – 1,1), I_c = (1,1, – 1) лежат на кривой, заданной уравнением (1), т. е. координаты указанных точек удовлетворяют этому уравнению. p

Непосредственно из геометрического определения кривой (1) видно, что она переходит сама в себя при изогональном сопряжении. В самом деле, если точка P лежит на кривой (1), то изогонально сопряженная с ней точка Q тоже лежит на кривой (1).

Точку F, с помощью которой строится кубическая кривая (1), будем называть центром вращения для этой кривой.

Кубика Дарбу. Центром вращения для этой кривой служит точка H, симметричная точке пересечения высот H относительно центра описанной окружности O. Легко проверить, что точка H имеет трилинейные координаты

(cos a – cos bcos g,cos b – cos gcos a, cos g – cos acos b),

где a, b, g — углы треугольника.

В трилинейных координатах кубика Дарбу задается уравнением

(cos a – cos bcos g)x(y2 – z2) + ј  =  0.

(Мы написали только коэффициент при x(y² – z²); коэффициенты при y(z² – x²) и при z(x² – y²) записываются очевидным образом.)

Кубика Дарбу проходит через следующие точки: ортоцентр и центр описанной окружности.

Кубика Дарбу допускает следующее геометрическое описание.

Теорема. Пусть A₁, B₁, C₁ — проекции точки D на прямые BC, CA, AB. Точка D лежит на кубике Дарбу тогда и только тогда, когда прямые AA₁, BB₁, CC₁ пересекаются в одной точке.

Доказательство. Согласно теореме Чевы прямые AA₁, BB₁, CC₁ пересекаются в одной точке тогда и только тогда, когда

AC1 · BA1 · CB1 = C1B · A1C · B1A,

где AC₁ и т. д. - ориентированные длины отрезков (т. е. числа AC₁ и C₁B имеют один и тот же знак, если точка C₁ лежит на отрезке AB, а если точка C₁ лежит вне отрезка AB, то эти числа имеют противоположные знаки).

Пусть (x,y,z) — нормированные трилинейные координаты точки D, т. е. x,y,z - расстояния от точки D до прямых BC, CA, AB с учетом знака. Легко проверить, что

AC1 =

zcos a + y sin a

и т. д. Поэтому прямые AA₁, BB₁, CC₁ пересекаются в одной точке тогда и только тогда, когда

(zcos a + y)(ycos g + x)(xcos b + z)  =  (zcos b + x)(xcos g + y)(ycos a + z).

Полученное уравнение легко преобразуется в уравнение кубики Дарбу. p

Замечание 1. Если равенство

AC1 · BA1 · CB1 = C1B · A1C · B1A

выполняется для некоторой точки D, то такое же равенство выполняется и для точки Dў, симметричной точке D относительно центра описанной окружности. Поэтому кубика Дарбу симметрична относительно центра описанной окружности.

Замечание 2. Несложно доказать, что прямые AA₁, BB₁, CC₁ пересекаются в одной точке тогда и только тогда, когда существует кривая второго порядка, касающаяся сторон треугольника (или их продолжений) в точках A₁, B₁, C₁.

Кубика Томсона. Центром вращения для этой кривой служит центр масс M. Напомним, что центр масс треугольника имеет трилинейные координаты (bc,ca,ab).

В трилинейных координатах кубика Томсона задается уравнением

bcx(y2 – z2) + cay(z2 – x2) + abz(x2 – y2) = 0.

По-другому это уравнение можно записать в виде

(cos a + cos bcos g)x(y2 – z2) + ј  =  0.

Кубика Томсона проходит через следующие точки: ортоцентр и центр описанной окружности, середины сторон, середины высот.

Из замечания 2 к теореме 1 видно, что кубика Дарбу допускает следующее геометрическое описание. Рассмотрим всевозможные кривые второго порядка, касающиеся сторон данного треугольника или их продолжений. Выделим среди них те кривые второго порядка, для которых перпендикуляры к сторонам треугольника в точках касания пересекаются в одной точке. Тогда точки пересечения этих перпендикуляров заметают кубику Дарбу. Можно доказать, что центры выделенных таким образом кривых второго порядка заметают кубику Томсона.

Кубика Мак-Кэя. Центром вращения для этой кривой служит центр описанной окружности O. Напомним, что центр описанной окружности имеет трилинейные координаты (cos a,cos b,cos g).

В трилинейных координатах кубика Мак-Кэя задается уравнением

cos ax(y2 – z2) + cos by(z2 – x2) + cos gz(x2 – y2) = 0.

Кубика Мак-Кэя проходит через следующие точки: ортоцентр и центр описанной окружности.

Теорема. Пусть вершины треугольника расположены в точках a, b, c единичной окружности на комплексной плоскости. Точка, соответствующая комплексному числу z, лежит на кубике Мак-Кэя тогда и только тогда, когда выполняется равенство

(z – a)(z – b)(z – c) = abc(a - z    – 1)(b - z    – 1)(c - z    – 1).

Доказательство. Пусть точки z и w изогонально сопряжены относительно данного треугольника. Тогда согласно теореме Морли (задача 29.34) точки z и w связаны соотношением

z + w + abc - z   - w    = a + b + c.

(2)

Следовательно,

- z    +  - w    +  - a   - b   - c   zw =  - a    +  - b    +  - c   .

(3)

Умножим обе части соотношения (3) на 

abc

- z

и вычтем из полученного выражение соотношение (2). В результате получим

w =  a + b + c – z – ( - a    +  - b    +  - c    –  - z   )abc - z   1 – |abcz|2 .

(4)

По определению кубики Мак-Кэя прямая zw проходит через центр описанной окружности, т. е. через начало координат. Это означает, что

w/

- w

=  z/

- z

. Выразив

w/

- w

с помощью соотношения (4), после несложных преобразований получим требуемое уравнение. p

Следствие. Кубика Мак-Кэя пересекает описанную окружность треугольника в трех точках, являющихся вершинами правильного треугольника. (Мы учитываем только точки пересечения, отличные от вершин исходного треугольника.)

Доказательство. Будем считать, что вершины треугольника расположены в точках единичной окружности на комплексной плоскости. Тогда для точки z, лежащей на описанной окружности треугольника, выполняется равенство

- z

= z – 1

. Поэтому точки пересечения кубики Мак-Кэя с описанной окружностью удовлетворяют уравнению

(z – a)(z – b)(z – c) =  – z – 3abc(z – a)(z – b)(z – c).

Если исключить вершины треугольника, то останутся точки, удовлетворяющие соотношению z³ =  – abc. Эти точки образуют правильный треугольник. p

Будем считать, что РPQR - величина угла, на который нужно повернуть против часовой стрелки вектор

® QP

так, чтобы он стал сонаправлен с вектором

® QR

.

Теорема. Точка M лежит на кубике Мак-Кэя тогда и только тогда, когда

РMAB + РMBC + РMCA =   p 2  + kp.

Доказательство. Снова будем считать, что вершины треугольника расположены на единичной окружности на комплексной плоскости. Положим a  =  РMAB, b  =  РMBC, g  =  РMCA. Пусть z - комплексное число, соответствующее точке M. Тогда

b – a z – a  ·  - z    –  - a   - b    –  - a    = e2ia,   т. е.    e2ia =  – b a - z    – 1 z – a .

Поэтому

e2i(a + b + g)  =   – abc (a - z    – 1)(b - z    – 1)(c - z    – 1) (z – a)(z – b)(z – c) .

Таким образом, точка z лежит на кубике Мак-Кэя тогда и только тогда, когда e^{2i(a + b + g)} =  – 1, т. е.

a + b + g  =

p 2

+ kp

. p

Легко проверить, что

РMAB + РMBC + РMCA + РMAC + РMCB + РMBA  =  (2n + 1)p.

Поэтому точка M лежит на кубике Мак-Кэя тогда и только тогда, когда

РMAB + РMBC + РMCA = РMAC + РMCB + РMBA + 2lp.

Отметим без доказательства следующее свойство кубики Мак-Кэя, которое обобщает теорему Фейербаха: описанная окружность треугольника, вершинами которого служат основания перпендикуляров, опущенных из любой точки кубики Мак-Кэя на стороны треугольника ABC (или на их продолжения), касается окружности девяти точек треугольника ABC.

Кубика Нейберга. Центром вращения для этой кривой служит бесконечно удаленная точка прямой OH. Иными словами, кубика Нейберга состоит из таких пар изогонально сопряженных точек P и Q, что прямая PQ параллельна прямой OH.

В трилинейных координатах кубика Нейберга задается уравнением

(cos a – 2cos bcos g)x(y2 – z2) + ј  =  0.

Кубика Нейберга является бесспорным лидером по количеству замечательных точек треугольника, через которые она проходит. Действительно, эта кривая проходит через следующие точки: центр описанной окружности; ортоцентр; вершины правильных треугольников, построенных на сторонах треугольника ABC (как внешним, так и внутренним образом); точки, симметричные вершинам треугольника ABC относительно его сторон; две точки, из которых стороны треугольника ABC видны под углом 60° или 120° (изогональные центры треугольника); две точки, для которых выполняется соотношение AX · BC = BX · CA = CX · AB (изодинамические центры треугольника).

Для рассмотренных выше кубик Дарбу, Томсона, Мак-Кэя и Нейберга центр вращения лежит на прямой Эйлера OH. Кубики, центры вращения которых лежат на прямой Эелера, можно построить и посредством другой геометрической конструкции ². Эта конструкция основывается на следующем утверждении.

Теорема. Пусть A₁, B₁, C₁ - основания перпендикуляров, опущенных из точки P на прямые BC, CA, AB, а треугольник A₂B₂C₂ получен из треугольника A₁B₁C₁ гомотетией с центром P и коэффициентом k. Тогда при фиксированном k № 0 точки P, для которых прямые AA₂, BB₂, CC₂ пересекаются в одной точке, заметают кубическую кривую.

Доказательство. Пусть (x : y : z) — трилинейные координаты точки P. Тогда точка A₂ имеет трилинейные координаты

ж и (1 – k)x : y + kxcos g : z + kxcos b ц ш .

Поэтому прямая AA₂ задается линейным уравнением с коэффициентами (0, – z – kxcos b,y + kxcos g). Следовательно, прямые AA₂, BB₂, CC₂ пересекаются в одной точке тогда и только тогда, когда обращается в нуль определитель

к к к к 0  – z – kxcos b y + kxcos g z + kycos a 0  – x – kycos g  – y – kzcos a x + kzcos b 0 к к к к  =

=  k(cos a – kcos bcos g)x(y2 – z2) + ј       p

При k = 1 получаем кубику Дарбу, при k =  – 1 - кубику Томсона, а при k = 2 — кубику Нейберга. Если подходить формально, то кубика Мак-Кэя этой конструкцией не охватывается. Но естественно считать, что она относится к случаю k = 0.

Посмотрим теперь по-другому на конструкцию, изложенную в формулировке теоремы. А именно, фиксируем точку P и будем считать число k переменным. Для каких точек P прямые AA₂, BB₂, CC₂ будут пересекаться в одной точке при всех k? И какие кривые будут заметать точки пересечения этих прямых?

Прямые AA₂, BB₂, CC₂ при всех k пересекаются в одной точке тогда и только тогда, когда точка P при всех k лежит на кубике

(cos a – kcos bcos g)x(y2 – z2) + ј  =  0.

Девять таких точек нам известны: A, B, C, I, I_a, I_b, I_c, H, O. Две кубические кривые, пересекающиеся в конечном числе точек, не могут иметь более девяти общих точек. Поэтому какие-то другие точки P могут обладать требуемым свойством лишь в исключительных случаях. Например, в случае правильного треугольника этим свойством обладают все точки, лежащие на высотах или их продолжениях.

Если P = A, B, C или H, то прямые AA₂, BB₂, CC₂ при всех k пересекаются в точке P. Интересные случаи соответствуют только центрам окружностей - описанной, вписанной и вневписанных.

Теорема. а ) Если P = O, то точки пересечения прямых AA₂, BB₂, CC₂ заметают прямую Эйлера OH.

б ) Если P = I (P = I_a), то точки пересечения прямых AA₂, BB₂, CC₂ заметают гиперболу, изогонально сопряженную прямой OI (прямой OI_a).

Доказательство. а) Пусть прямые AA₂, BB₂, CC₂ пересекаются в точке с трилинейными координатами (xў : yў : zў). Уравнение прямой AA₂ показывает, что

yў zў  =   y + kxcos g z + kxcos b  =   cos b + kcos acos g cos g + kcos acos b ,

поскольку точка O имеет трилинейные координаты (x : y : z) = (cos a : cos b : cos g). Поэтому

(xў : yў : zў)  =

= (cos a + kcos bcos g :  cos b + kcos acos g : cos g + kcos acos b).

Все такие точки лежат на прямой OH.

б) Ограничимся разбором случая P = I. В этом случае (x : y : z) = (1 : 1 : 1), поэтому

yў zў  =   y + kxcos g z + kxcos b  =   1 + kcos g 1 + kcos b .

Таким образом, точка, изогонально сопряженная точке (xў : yў : zў), имеет трилинейные координаты

(1 + cos a : 1 + kcos b : 1 + kcos g).

Все такие точки лежат на прямой OI.

Сноски:

¹ Cundy H. M., Parry C. F. Some cubic curves associated with a triangle. — Journal of Geometry, 1995. Vol. 53. P. 41–66.

² Pinkernell G. M. Cubic curves in the triangle plane. — Journal of Geometry, 1996. Vol. 55. P. 141–161.

Глава 30. § 1 |	Оглавление |

Copyright © 2002 МЦНМО

Внимание! Данное издание содержит опечатки! Исправленные исходные файлы книги и файлы нового издания доступны со страницы автора. Заказ книги: biblio@mccme.ru.